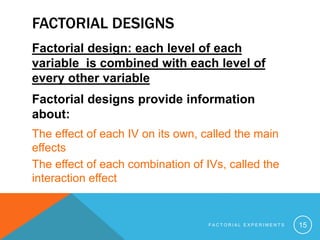
This document introduces factorial experiments through two examples. The first example is a 2x2 between-subjects design that examines the effects of violent video exposure and gender on feelings of aggression. It finds main effects for both video and gender, but no interaction. The second example is also a 2x2 between-subjects design examining the interactive effects of alcohol consumption and sleep deprivation on driving performance. It finds main effects for both variables and a significant interaction. The document further discusses more complex factorial designs with additional factors and levels. Factorial designs allow examination of multiple variables and their interactions simultaneously in a single experiment.

2. AIM: TO INTRODUCE THE PRINCIPLES OF
A FACTORIAL EXPERIMENT
F A C T O R I A L E X P E R I M E N T S 2
Factorial
Experiments
Example 1 Overview Example 2
Other
designs

3. EXAMPLE
Bushman et al (1971):
Do adults feel more violent after seeing
violence?
Do males generally feel more violent then
females?
Are males affected more by seeing violence
than females?
F A C T O R I A L E X P E R I M E N T S 3

4. EXAMPLE
Independent variables.
(1) Violence of video with two levels:
Violent video & Neutral video.
(2) Gender with two levels:
Male & Female.
Dependent variable:
Feelings of aggression
Measured by the number of aggressive
associates to ambiguous words e.g. cuff - “shirt”
or “punch”.
F A C T O R I A L E X P E R I M E N T S 4

5. EXAMPLE
This is a factorial experiment
Each level of each independent variable occurs
with each level of the other factor:
male subjects see the violent video
male subjects see the neutral video
female subjects see the violent video
female subjects see the neutral video
It is also an independent groups
experiment
Different subjects in each condition
F A C T O R I A L E X P E R I M E N T S 5

6. SUMMARY OF EXPERIMENT
Violence of Video
(IV1)
Neutral
(level 1)
Violent
(level 2)
Gender of
Subject (IV2)
Male (level 1) Group 1 Group 2
Female (level 2) Group 3 Group 4
F A C T O R I A L E X P E R I M E N T S 6
Experiment referred to as a: 2 x 2 unrelated (between subjects)
experiment

7. EXAMPLE
Design permits three hypotheses:
1 Main effect
The effect of type of video on aggression
Seeing a violent video will produce more feelings of
aggression than seeing a neutral video
2 Main effect
The effect of gender on aggression
Males will generally feel more aggressive then
females, regardless of video
F A C T O R I A L E X P E R I M E N T S 7

8. EXAMPLE
3 Interaction effect
The interaction of type of video and
gender
Relative to the neutral video, violent
video affects males more than
females.
F A C T O R I A L E X P E R I M E N T S 8

9. EXAMPLE
Type of Video
neutral
video
violent
video
Condition
Means
(gender)
Gende
r
Male 6.2 7.7 6.95
Female 5.1 6.5 5.80
Condition
Means
(video)
5.65 7.10
F A C T O R I A L E X P E R I M E N T S 9

10. EXAMPLE
Result 1 – Main effect
The effect of type of
video on aggression
• 5.65 (neutral) vs 7.1
(violent)
• The violent video
produces a higher
aggression score than
the neutral video
• This result needs to be
confirmed with a
statistical test
5.65
7.10
0
1
2
3
4
5
6
7
8
9
10
Aggression
score
Video type
Neutral
Violent
F A C T O R I A L E X P E R I M E N T S 10

11. EXAMPLE
Result 2 – Main effect
• The effect of gender on
aggression
• 6.95 (male) vs 5.80
(female)
• Males produce higher
aggression scores than
females
• This result needs to be
confirmed with a
statistical test
6.95
5.8
0
1
2
3
4
5
6
7
8
9
10
Aggression
score
Gender
male
female
F A C T O R I A L E X P E R I M E N T S 11

12. EXAMPLE
Result 3 – Interaction
The interaction of type of
video and gender
There seems to be no
interaction effect (if lines are
parallel usually the case)
i.e. The violent video doesn’t
seem to have a greater effect on
males than females
0
1
2
3
4
5
6
7
8
Neutral Violent
Aggression
Score
Video Type
Figure 1. Effect of video type
and gender on aggression
scores
Male
Female
F A C T O R I A L E X P E R I M E N T S 12

13. PROGRESSION POINT
F A C T O R I A L E X P E R I M E N T S 13
Factorial
Experiments
Example 1 Overview Example 2
Other
designs

14. FACTORIAL DESIGNS
Single factor experiments deal with one
independent variable
Most psychological phenomena are
governed by several independent variables
Often these variables have combined or
interactive effects
Thus need to look at several factors in the
same experiment
Use Factorial Designs
F A C T O R I A L E X P E R I M E N T S 14

15. FACTORIAL DESIGNS
Factorial design: each level of each
variable is combined with each level of
every other variable
Factorial designs provide information
about:
The effect of each IV on its own, called the main
effects
The effect of each combination of IVs, called the
interaction effect
F A C T O R I A L E X P E R I M E N T S 15

16. FACTORIAL DESIGNS
Complexity can vary in (1) number of
independent variables and (2) number of
levels of each independent variable
Describing a factorial design:
m x n – two Independent variables, one with m
levels, the other with n levels
l x m x n – three independent variables, one with
l levels, one with m levels and one with n levels
See over for examples
F A C T O R I A L E X P E R I M E N T S 16

17. FACTORIAL DESIGNS
Video type (IV1)
neutral violent
Gender
(IV2)
male
female
F A C T O R I A L E X P E R I M E N T S 17
NOTE: If there is no interaction the results of the simplest
design (2 x 2) can be interpreted directly without further post hoc
comparisons
Example: A 2 x 2 factorial design

18. FACTORIAL DESIGNS
F A C T O R I A L E X P E R I M E N T S 18
Video type (IV1)
caring neutral violent
Gender
(IV2)
male
female
Example: A 2 x 3 factorial design
When there are three or more levels of an independent variable
post hoc tests will be required if the main effect involves that
variable, or if there is an interaction

19. FACTORIAL DESIGNS
Advantages of Factorial Designs
Economical - looks at more than one variable at a
time.
Interactive - can look at the combined effects of
variables
Caution with factorial designs
Interpretation of results becomes problematic as:
the number of levels of each variable increases
E.g. 2 x 2 ; 3 x 3; 4 x 4; etc
the number of factors increases
E.g. 2 x 2; 2 x 2 x 2; 2 x 2 x 2 x 2
F A C T O R I A L E X P E R I M E N T S 19

20. PROGRESSION POINT
F A C T O R I A L E X P E R I M E N T S 20
Factorial
Experiments
Example 1 Overview Example 2
Other
designs

21. EXAMPLE 2 (WITH SIGNIFICANT
INTERACTION)
Hypothetical experiment:
Effects of alcohol and sleep deprivation on
driving performance
Independent variables
1. Amount of alcohol: 0 mls. vs 50 mls.
2. Amount of sleep deprivation: 4 hrs vs 12 hrs
Dependent variable
Number of mistakes on simulator
F A C T O R I A L E X P E R I M E N T S 21

22. EXAMPLE
Sleep deprivation
4 hrs 12 hrs Condition
Means
(alcohol)
Amount
of
Alcohol
zero millilitres 10.67 12.67 11.67
50 millilitres 15.00 26.00 20.50
Condition Means
(sleep
deprivation)
12.84 19.34
F A C T O R I A L E X P E R I M E N T S 22

23. EXAMPLE
Thee results have to be tested: two main
effects and one interaction
1. Main effect of alcohol
2. Main effect of sleep deprivation
3. Interaction between alcohol and sleep
deprivation
F A C T O R I A L E X P E R I M E N T S 23

24. EXAMPLE 2: MAIN EFFECT OF ALCOHOL
11.67
20.5
0
5
10
15
20
25
0 mls 50 mls
Number of
errors
Amount of alcohol
F A C T O R I A L E X P E R I M E N T S 24
Figure 1: Effect of amount of alcohol on number of errors

25. EXAMPLE 2 MAIN EFFECT OF SLEEP
DEPRIVATION
12.84
19.3
0
5
10
15
20
25
4 hrs 12 hrs
Number of
errors
Amount of sleep deprivation
F A C T O R I A L E X P E R I M E N T S 25
Figure 2: Effect of amount of sleep deprivation on number of errors

26. EXAMPLE 2 INTERACTION
10.67
12.67
15
26
0
5
10
15
20
25
30
4 hrs 24 hrs
Number of
errors
Amount of sleep deprivation
0 mls
50 mls
F A C T O R I A L E X P E R I M E N T S 26
Figure 3: Effect of the interaction of amount of alcohol and amount
of sleep deprivation on number of errors

27. PROGRESSION POINT
F A C T O R I A L E X P E R I M E N T S 27
Factorial
Experiments
Example 1 Overview Example 2
Other
designs

28. OTHER FACTORIAL DESIGNS: MORE
LEVELS
Sleep deprivation
4 hrs 12 hrs 24 hrs
Amount
of alcohol
0 mls Group 1 Group 2 Group 3
25 mls Group 4 Group 5 Group 6
50 mls Group 7 Group 8 Group 9
F A C T O R I A L E X P E R I M E N T S 28
This is a 3 x 3 unrelated (between subjects) design
Yields: Two main effects and one interaction effect . Post hoc comparisons are
needed to see where the differences lie because one variable has three levels

29. OTHER FACTORIAL DESIGNS: MORE
INDEPENDENT VARIABLES
4 hrs sleep deprivation 12 hrs sleep
deprivation
caffeine no caffeine caffeine no caffeine
0 mls
alcohol
Group 1 Group 2 Group 3 Group 4
50 mls
alcohol
Group 5 Group 6 Group 7 Group 8
F A C T O R I A L E X P E R I M E N T S 29
This is a 2 x 2 x 2 unrelated design: variables are (1) sleep deprivation, (2)
amount of alcohol and (3) amount of caffeine
Yields: three main effects and four interaction effects. Post hoc comparisons
may be needed

30. OTHER FACTORIAL DESIGNS: MIXED
Sleep deprivation
4 hrs 24 hrs
Amount
of
Alcohol
0 millilitres Group 1 Group1
50 millilitres Group 2 Group 2
F A C T O R I A L E X P E R I M E N T S 30
This is a 2 x 2 mixed design: same subjects for one variable; different
subjects for the other variable
Yields two main effects and one interaction effect but analysis is different

31. LEARNING OUTCOMES
Explain why factorial designs are important
Identify the information that comes from a
factorial design
Explain the terms “Main Effects” and “Interaction
Effect”
Identify the advantages and cautions of factorial
designs
Outline the nature of more complex designs
F A C T O R I A L E X P E R I M E N T S 31

32. READING
Howitt, D & Cramer, D (1997) An Introduction to
Statistics in Psychology. Chapter 22 (two-way
analysis of variance for unrelated scores) and
chapter 24 (More complex designs).
Howitt, D & Cramer, D (1999) Introduction to SPSS
in Psychology. Chapter 22 (two-way analysis of
variance for unrelated) and (optional) chapter 24
(analysis of covariance and two-way mixed
designs).
F A C T O R I A L E X P E R I M E N T S 32