The document discusses Wigner distributions and generalized transverse momentum dependent parton distributions (GTMDs) in light-cone quark models. It presents results for Wigner distributions of unpolarized quarks in an unpolarized nucleon, showing an anisotropic transverse momentum distribution. General relations between GTMDs, generalized parton distributions, and transverse momentum dependent parton distributions are explored in different quark models. The document also examines two definitions of quark orbital angular momentum in terms of light-cone wavefunctions and finds they yield the same total angular momentum but different distributions as a function of longitudinal momentum fraction in quark models.

1. Wigner Distributions
in
Light-Cone Quark Models
Barbara Pasquini
Pavia U. & INFN, Pavia
in collaboration with
Cédric Lorcé
Mainz U. & INFN, Pavia

2. Outline
Generalized Transverse Momentum Dependent Parton Distributions (GTMDs)
Wigner Distributions
FT   b
 Results for Wigner distributions in light-cone quark models
 unpolarized quarks in unpolarized nucleon (generalized transverse charge density)
 General formalism for the 3-quark contribution to GTMDs
 Relations between GPDs and TMDs
 Relations among TMDs in various 3-quark models
 Orbital Angular Momentum in terms of LCWF: Ji’s vs. Jaffe-Manohar’s definition

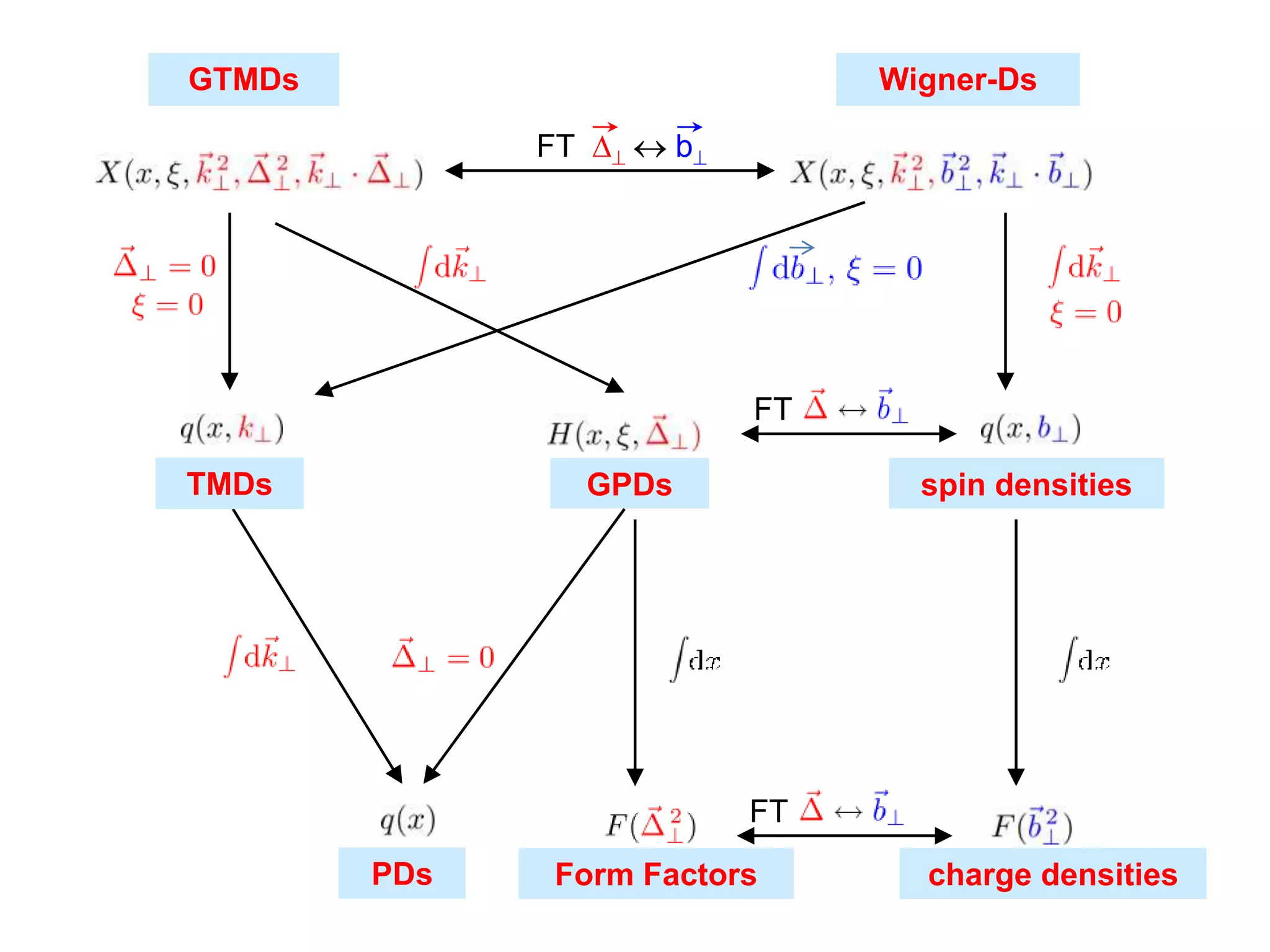
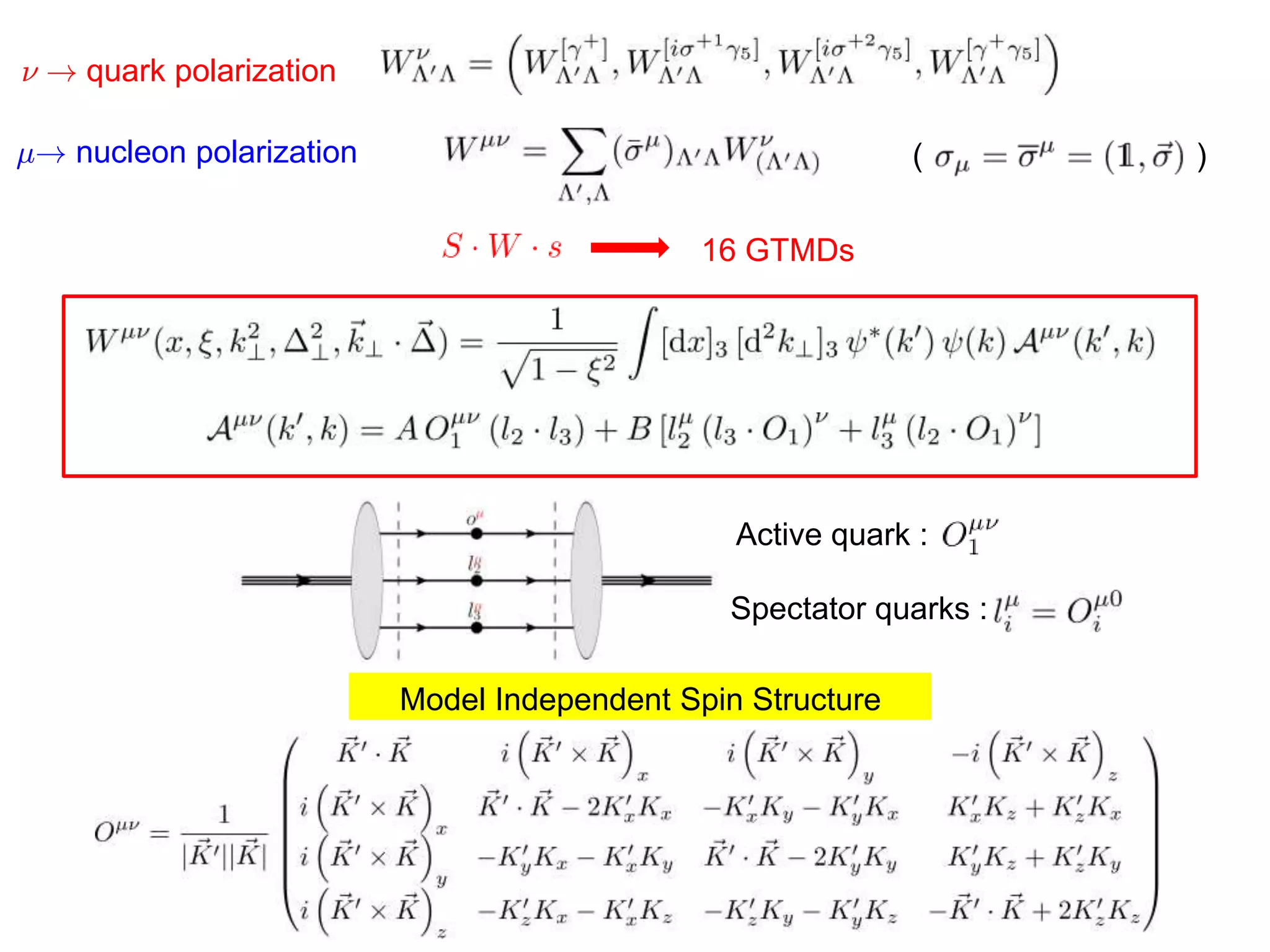
3. Generalized TMDs
GTMDs
 Complete parametrization : 16 GTMDs
[Meißner, Metz, Schlegel (2009)]
 Fourier Transform : 16 Wigner distributions
[Belitsky, Ji, Yuan (2004)]
x: average fraction of quark
longitudinal momentum
»: fraction of longitudinal
momentum transfer
k?: average quark transverse momentum ¢: nucleon momentum transfer

4. GPDs
PDs Form Factors
FT   b
GTMDs Wigner-Ds
spin densities
FT
charge densities
FT
TMDs

5. Wigner Distributions
 Quantum phase-space distribution: most complete information on wave function
quantum molecular dynamics, signal analysis, quantum info, optics, image processing,…
 real functions, but in general not-positive definite
 Wigner distributions in QCD:
at »=0 ! diagonal in the Fock-space
N N
N=3 ! overlap of quark light-cone wave-functions
not probabilistic interpretation
correlations of quark momentum and position in the transverse plane
as function of quark and nucleon polarizations
 no known experiments can directly measure them ! needs phenomenological models
[Wigner, (1932)]

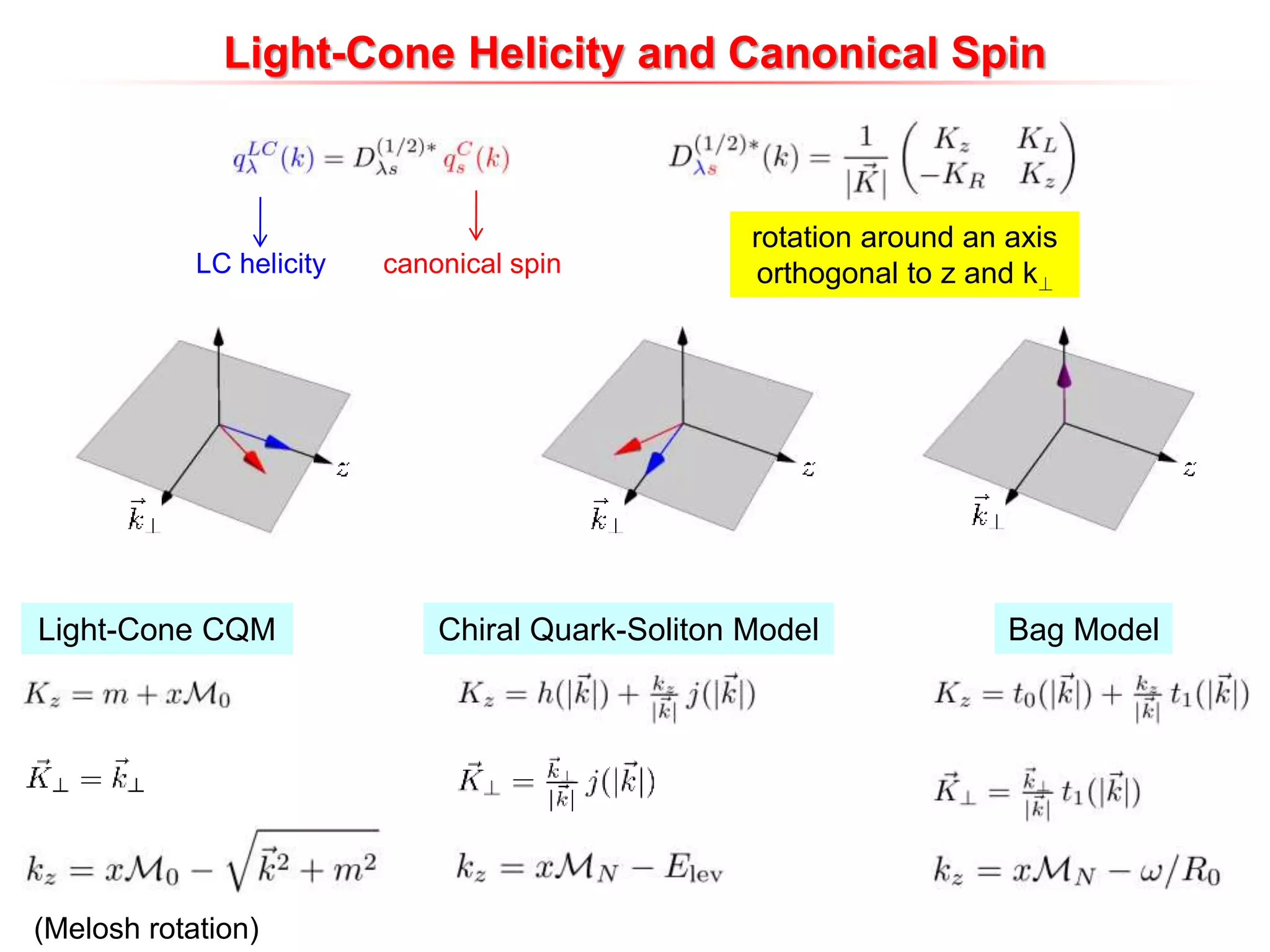
6. Light-Cone Quark Models
invariant under boost, independent of P
internal variables:
LCWF:
[Brodsky, Pauli, Pinsky, ’98]
Bag Model, ÂQSM, LCQM, Quark-Diquark and Covariant Parton Models
momentum wf spin-flavor wf rotation from canonical
spin to light-cone spin
Common assumptions :  No gluons
 Independent quarks

7. LC helicity canonical spin
rotation around an axis
orthogonal to z and k?
Light-Cone CQM Chiral Quark-Soliton Model Bag Model
(Melosh rotation)
Light-Cone Helicity and Canonical Spin

8. º ! quark polarization
16 GTMDs
¹! nucleon polarization ( )
Twist-2 operators
Light-cone gauge A+=0 Wilson line r reduces to the identity

9. Quark line :
3-Quark Overlap representation
Active quark : Spectator quarks :
Model Independent Spin Structure

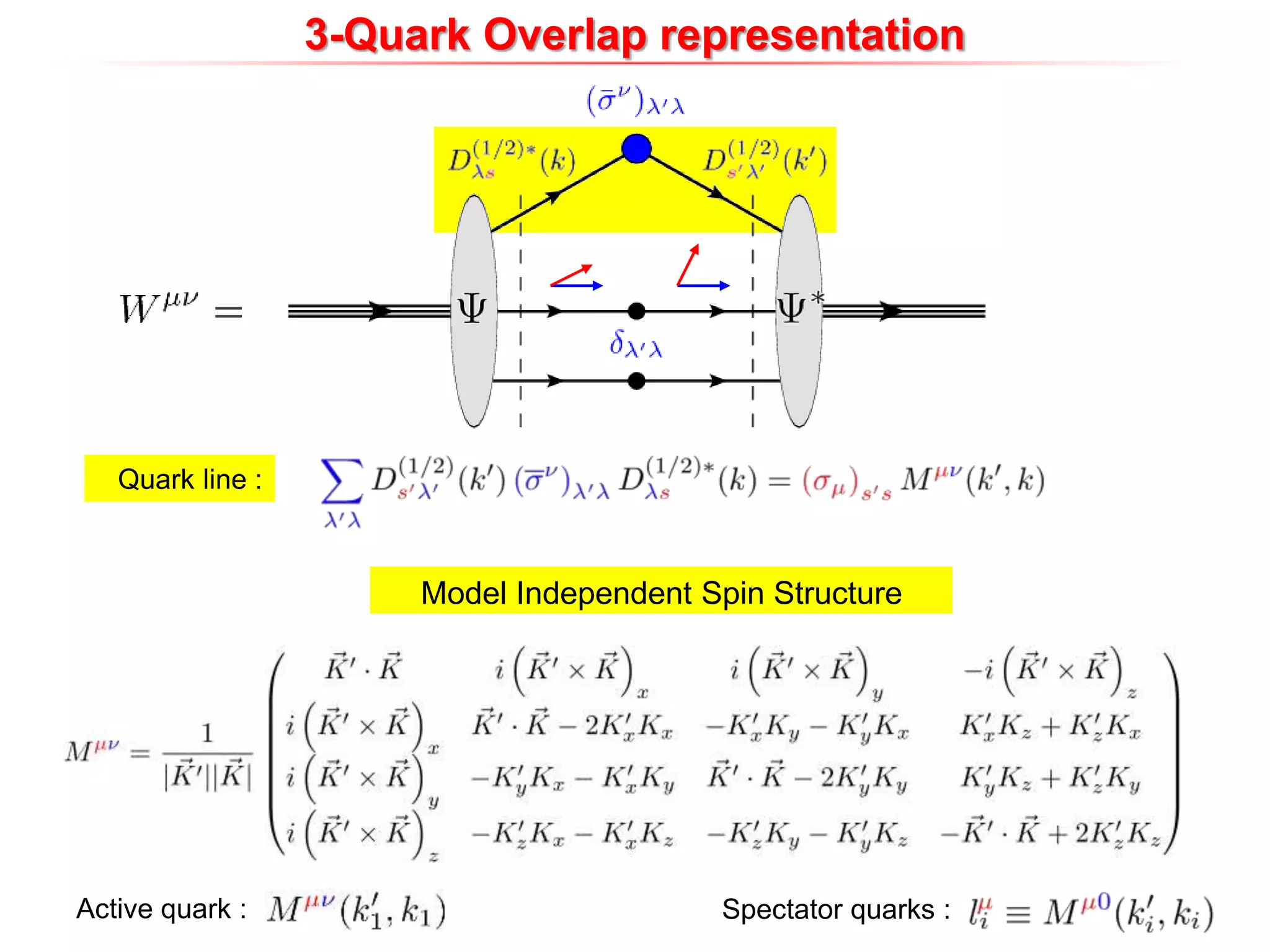
10. Assumption :  symmetry
[C.Lorce’, B. Pasquini, M. Vanderhaeghen (in preparation)]
3-Quark Overlap representation
16 GTMDs

11. parameters fitted to anomalous
magnetic moments of the nucleon
: normalization constant
[Schlumpf, Ph.D. Thesis,
hep-ph/9211255]
 momentum-space wf
 spin-structure:
(Melosh rotation)
 SU(6) symmetry
Light-Cone Constituent Quark Model
free quarks
Applications of the model to:
GPDs and form factors: BP, Boffi, Traini (2003)-(2005);
TMDs: BP, Cazzaniga, Boffi (2008); BP, Yuan (2010);
Azimuthal asymmetries: Schweitzer, BP, Boffi, Efremov (2009)

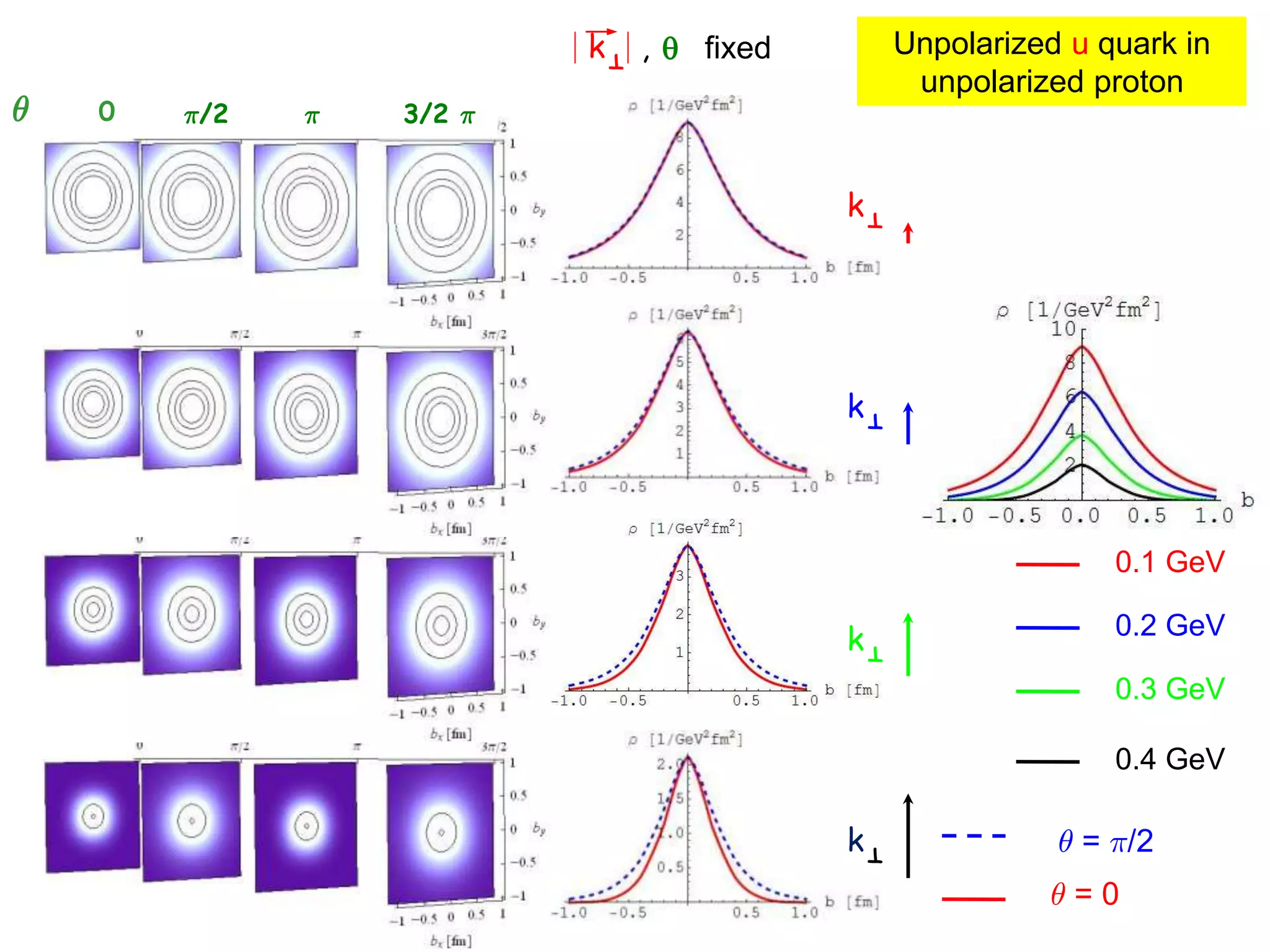
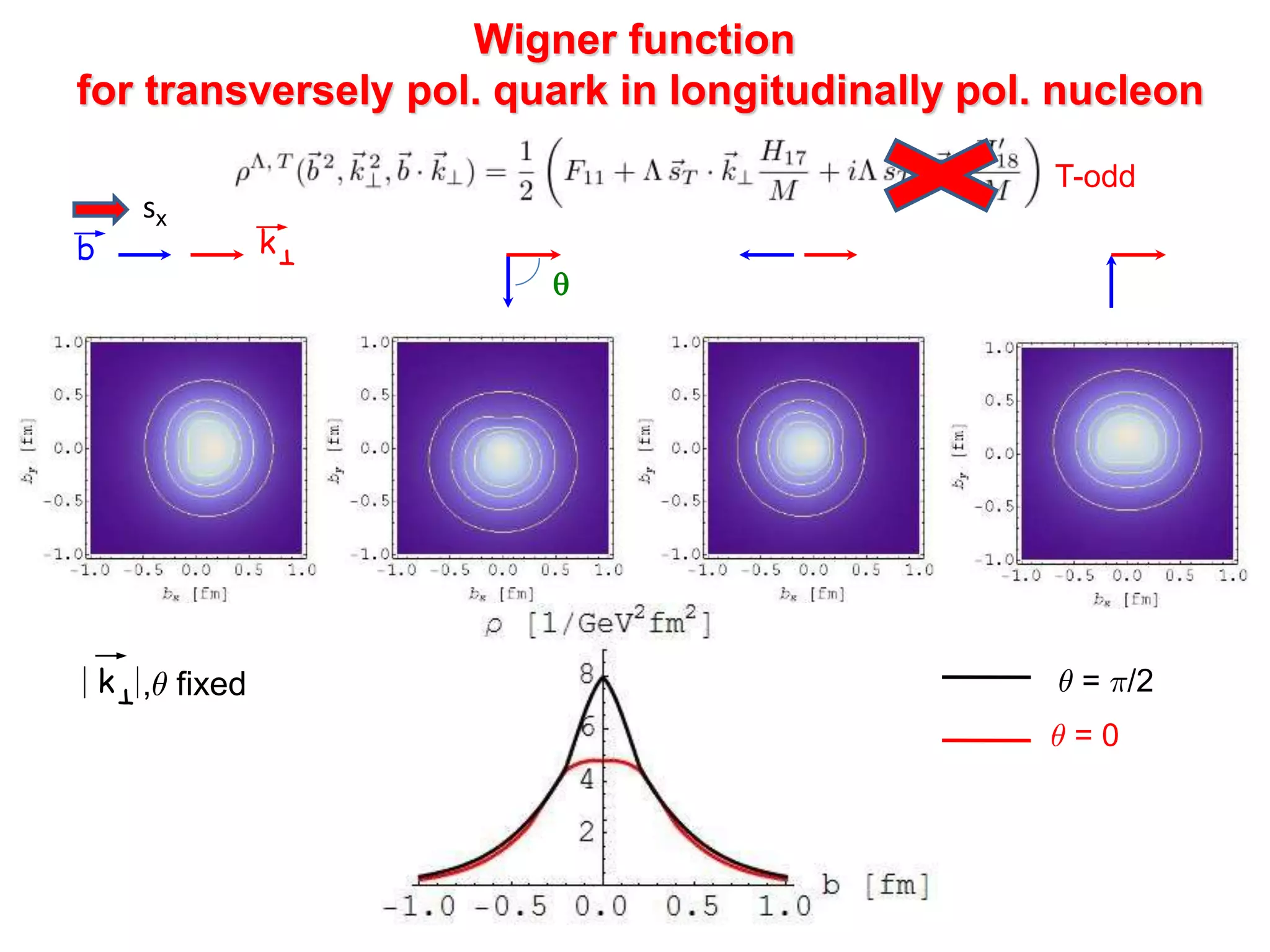
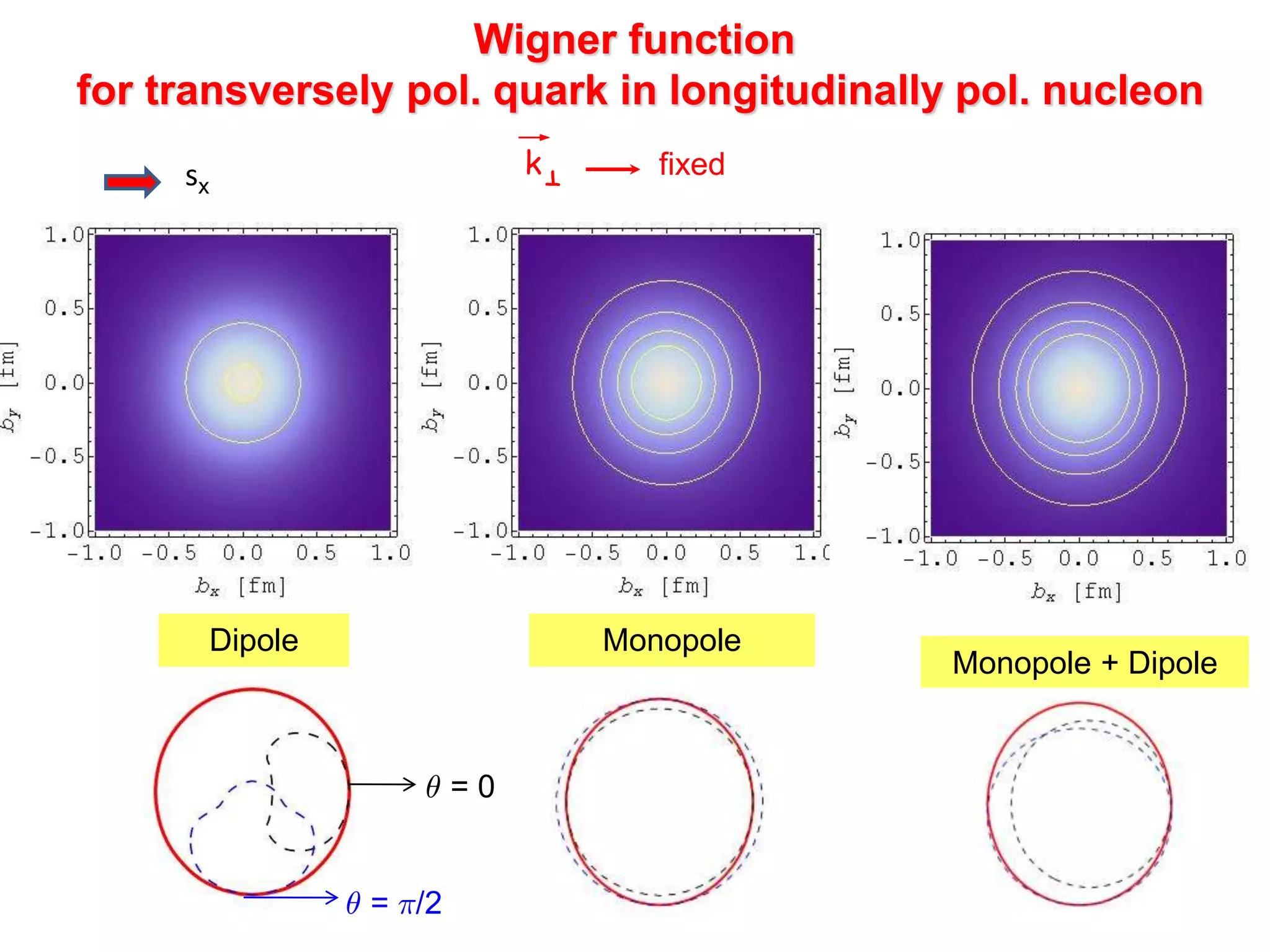
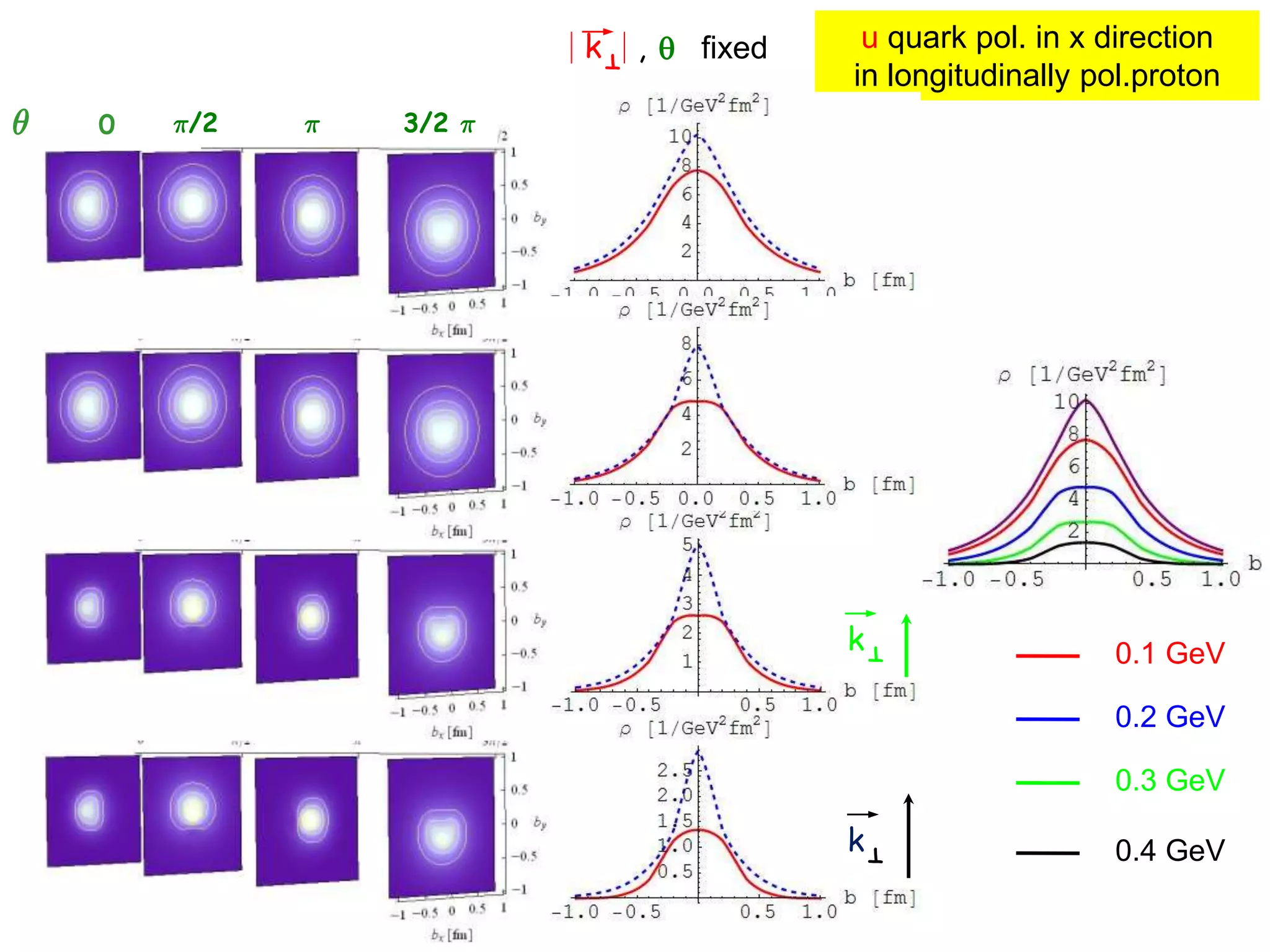
12. T
q
kT
b
k , µ fixed
Wigner function
for unpolarized quark in unpolarized nucleon
µ = ¼/2
µ = 0
[C.Lorce’, B. P. (in preparation)]

13. µ 0 ¼/2 ¼ 3/2 ¼
kT
kT
kT
Unpolarized u quark in
unpolarized proton
,
kT q fixed
kT
0.1 GeV
0.2 GeV
0.3 GeV
0.4 GeV
µ = ¼/2
µ = 0

14. = +
kT
kT fixed
Unpolarized u quark in
unpolarized proton
Generalized Transverse Charge Densities
µ = ¼/2
µ = 0

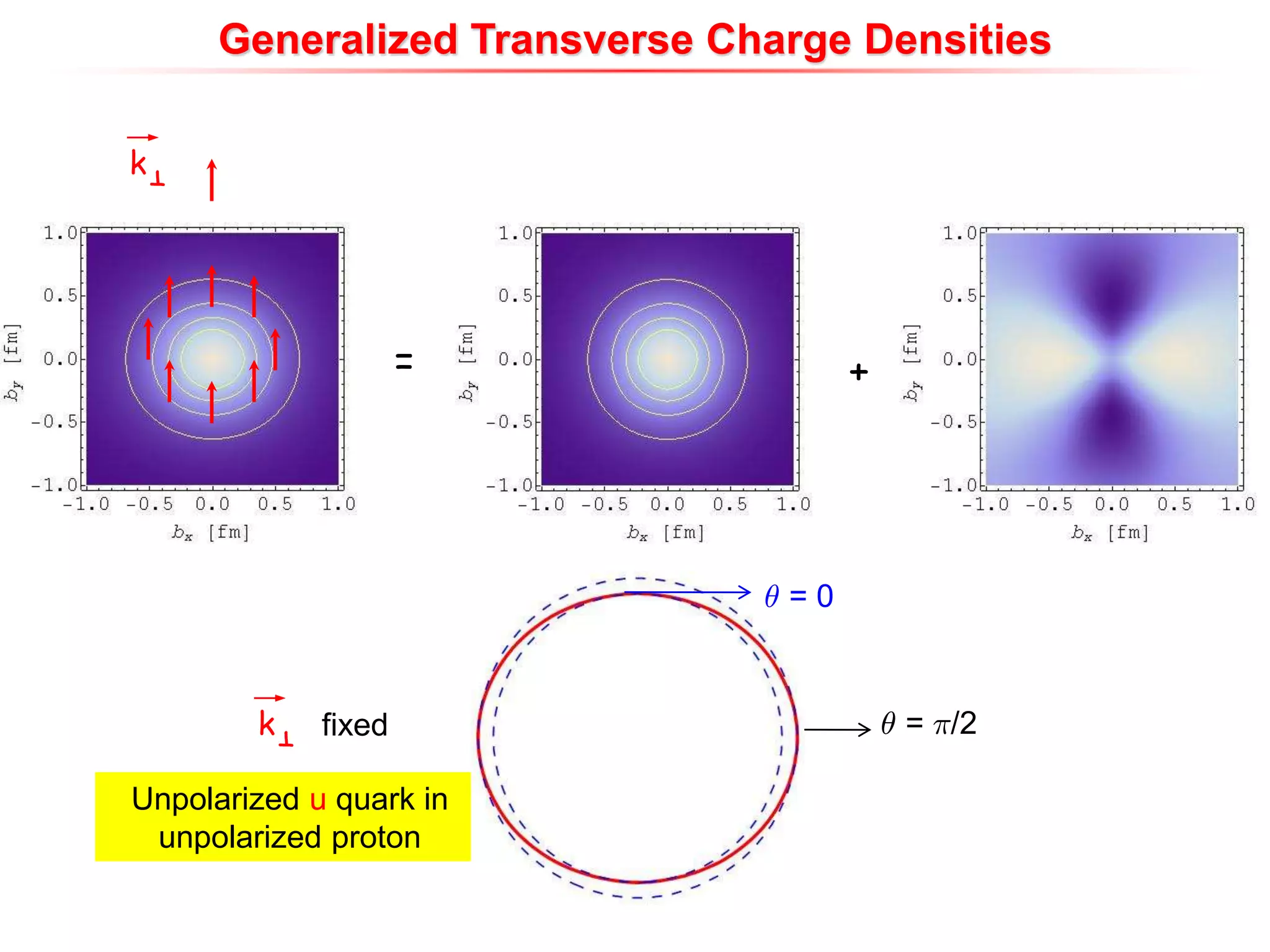
15. unpolarized u and d quarks in
unpolarized proton
proton neutron
[Miller (2007); Burkardt (2007)]
charge distribution in the
transverse plane
 Integrating over b ? TMD
 Integrating over k ? charge density in the transverse plane b?

16. GTMDs
GPDs TMDs
GPDs and TMDs probe the same overlap of quark LCWFs in different kinematics
at »=0
UU
LL
TT
UT
TU
TT
LT 0 0
TL
nucleon quark

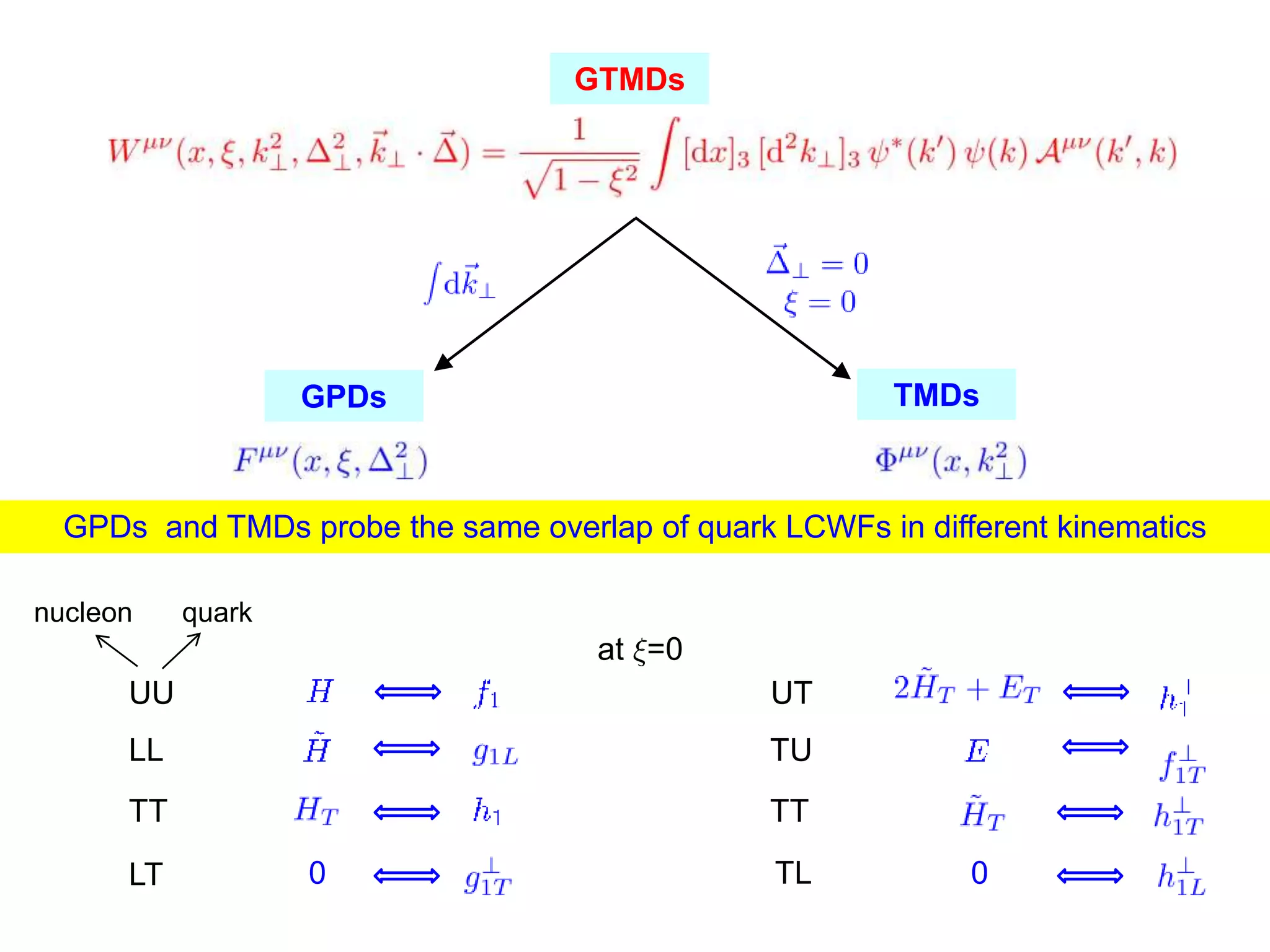
17. Relations between GPDs and TMDs in Quark Models
GPDs and TMDs probe the same overlap of LCWFs in different kinematics
there exist relations in particular kinematical limits?
UU
LL
TT
Trivial Relations
Non-Trivial Relations
TT
valid also in spectator model : Meissner, Metz, Goeke, PRD76(2007)
(with a factor 3 instead of 2)
Model dependent relations
SSA= GPDFSI
[Burkardt, Hwang, 2003; Burkardt, 2005]
valid for both Sivers and Boer-Mulders functions in spectator model, but breaks down at higher-orders

18. LT 0 0
TL
GPDs at »=0 vanish because of time-reversal invariance
sx
up down
BP, Cazzaniga, Boffi, PRD78 (2008); Lorce`, BP, in preparation
Haegler, Musch, Negele, Schaefer, Europhys. Lett. 88 (2009)
Light-cone quark model: ! consistent with lattice calculations

19. **
*
*
*
*
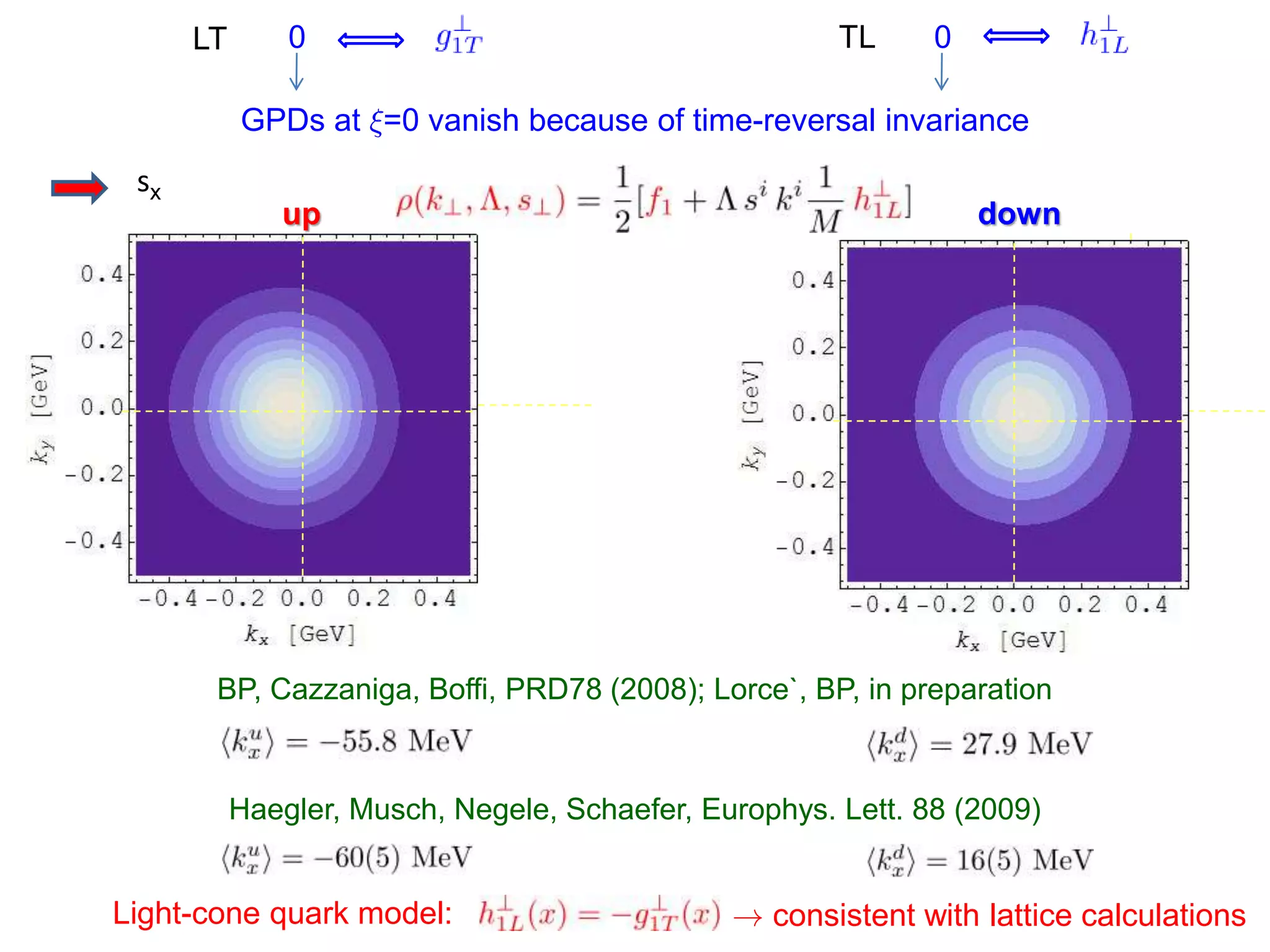
Flavor-dependent
Flavor-independent
Linear relations Quadratic relation
Bag
ÂQSM
LCQM
S Diquark
AV Diquark
Cov. Parton
Quark Target
[Jaffe & Ji (1991), Signal (1997), Barone & al. (2002), Avakian & al. (2008-2010)]
[Lorcé & Pasquini (in preparation)]
[Pasquini & al. (2005-2008)]
[Ma & al. (1996-2009), Jakob & al. (1997), Bacchetta & al. (2008)]
[Ma & al. (1996-2009), Jakob & al. (1997)] [Bacchetta & al. (2008)]
[Efremov & al. (2009)]
[Meißner & al. (2007)]
*
*
*
*
*
*
Relations among TMDs in Quark Models
Common assumptions :  No gluons
 Independent quarks

20. Quark polarization
Nucleon
polarization
LC helicity
Quark polarization
Nucleon
polarization
Canonical spin
Light-cone Helicity and Canonical Spin
rotation around an axis
orthogonal to z and k? of
an angle µ=µ(k)
 Rotations in light-front dynamics depend on the interaction, while are kinematical in canonical
quantization we study the rotational symmetries for TMDs in the basis of canonical spin

21. Rotational Symmetries in Canonical-Spin Basis
 Spherical symmetry and SU(6) spin-flavor symmetry
[C. Lorce’, B.P., in preparation]
 Spherical symmetry: invariance for any spin rotation
 Cilindrical symmetry around Ty k k?
 Cilindrical symmetry around z direction
nucleon spin
quark spin

22. Orbital Angular Momentum
[ X. Ji, PRL 78, (1997) ] [ R.L. Jaffe, NPB 337, (1990) ]
gauge invariant,
but contains interactions through
the gauge covariant derivative
not gauge invariant,
but diagonal in the LCWFs basis
not unique decomposition
Ji’s sum rule
quark orbital angular momentum:
What is the difference between the two definitions in a quark model without gauge fields?
scalar diquark model: M. Burkardt, PRD79, 071501 (2009); LCCQM: BP, F. Yuan, in preparation

23. Three Quark Light Cone Amplitudes
6 independent wave function amplitudes:
isospin symmetry
parity
time reversal
total quark helicity Jq
 classification of LCWFs in angular momentum components
Jz = Jz
q + Lz
q
[Ji, J.P. Ma, Yuan, 03;
Burkardt, Ji, Yuan, 02]
Lz
q =2
Lz
q =1
Lz
q =0
Lz
q = -1
Lz
q = 1
Lz
q= 0
Lz
q = 2
Lz
q = -1

24. Quark Orbital Angular Momentum
 Jaffe-Manohar definition:
 Ji’s definition:
overlap of LCWFs with ¢Lz=0
interference between LCWFs with different Lz
¢Lz=0 ¢Lz=0
¢Lz= 1
it is not trivial to have the same orbital angular momentum for the quark contribution
Jaffe-Manohar and Ji OAM should coincide when A=0
! no-gluons, only quark contribution

25. Distribution in x of Orbital Angular Momentum
Definition of Jaffe and Manohar: contribution from different partial waves
up down
TOT
Lz=0
Lz=-1
Lz=+2
Lz=-1
Ji
Jaffe-Manohar
total result, sum of up and down contributions: Jaffe-Manohar’s vs. Ji’s definition
even in a model without gauge fields the two definitions give different distributions in x

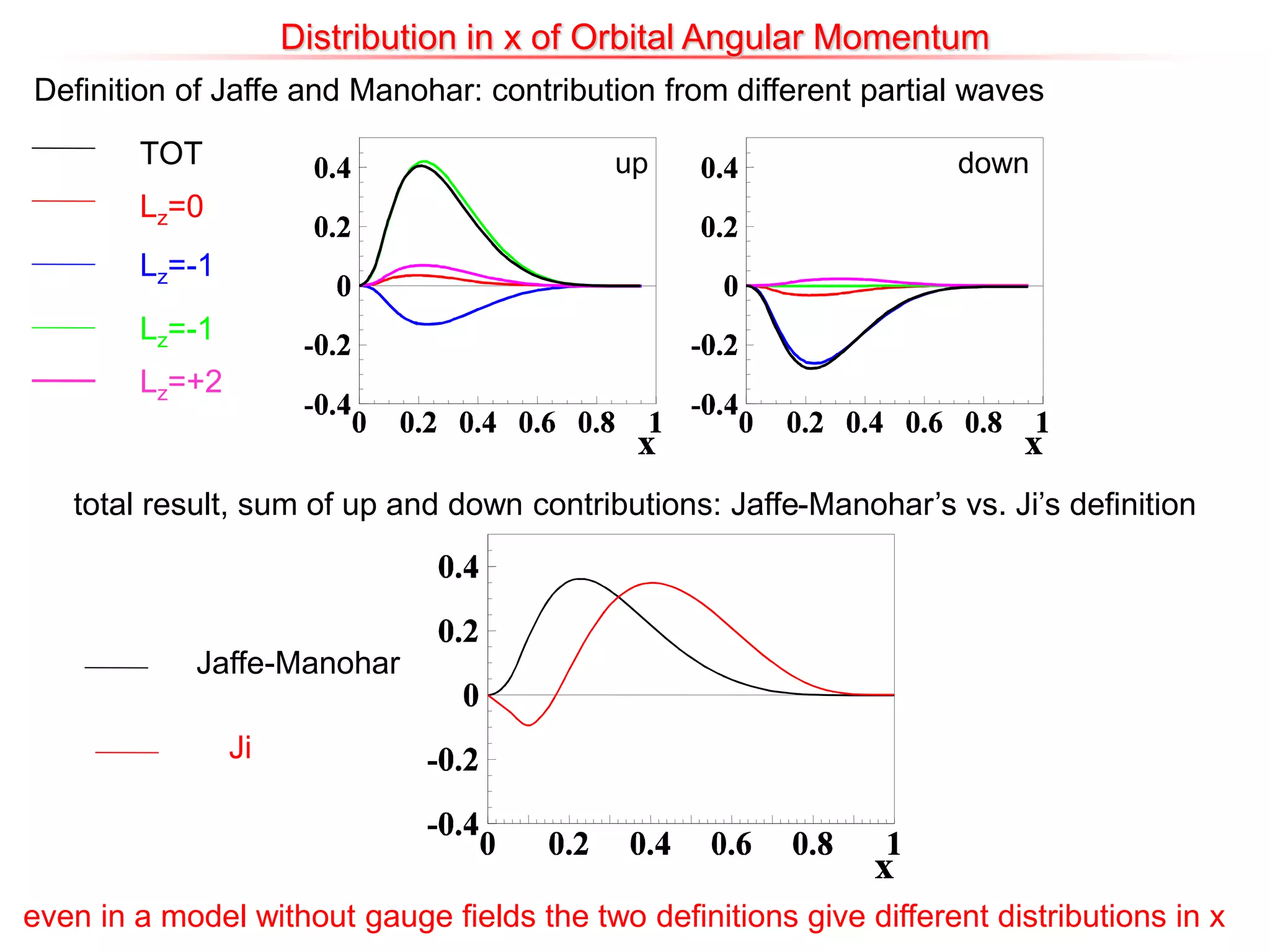
26. Orbital Angular Momentum
 Definition of Jaffe and Manohar: contribution from different partial waves
 Definition of Ji:
= 0 ¢ 0.62 + (-1) ¢ 0.14 + (+1) ¢ 0.23 + (+2) ¢ 0.018 = 0.126
[BP, F. Yuan, in preparation]
[scalar diquark model: M. Burkardt, PRD79, 071501 (2009)]

27. Summary
 GTMDs $ Wigner Distributions
- the most complete information on partonic structure of the nucleon
 General Formalism for 3-quark contribution to GTMDs
- applicable for large class of models: LCQMs, ÂQSM, Bag model
 Results for Wigner distributions in the transverse plane
- anisotropic distribution in k? even for unpolarized quarks in unpolarized nucleon
 GPDs and TMDs probe the same overlap of 3-quark LCWF in different kinematics
 Relations of TMDs in a large class of models due to rotational symmetries in the
quark-spin space
- give complementary information useful to reconstruct the nucleon wf
- useful to test them with experimental observables in the valence region
 Orbital Angular Momentum in terms of LCWFs:
- in quark models, the total OAM (but not the distributions in x) is the same from JI
and Jaffe-Manohar definitions

28. Backup

29. Wigner function
for transversely pol. quark in longitudinally pol. nucleon
µ = ¼/2
µ = 0
T-odd
q
kT
b
sx
kT ,µ fixed

30. Wigner function
for transversely pol. quark in longitudinally pol. nucleon
Dipole
µ = 0
µ = ¼/2
Monopole + Dipole
kT fixed
sx
Monopole

31. ¼ 3/2 ¼
u quark pol. in x direction
in longitudinally pol.proton
,
kT q fixed
0.1 GeV
0.2 GeV
0.3 GeV
0.4 GeV
kT
kT
kT
kT
µ 0 ¼/2

32. 16 GTMDs
º ! quark polarization
¹! nucleon polarization
Active quark :
Spectator quarks :
Model Independent Spin Structure
( )

33. Orbital Angular Momentum in the Light-Front
 Light-cone Gauge A+=0 and advanced boundary condition for A
 generalization of the relation for the anomalous magnetic moment:
[Brodsky, Drell, PRD22, 1980]
complex LCWFs due to FSI/ISI [Brodsky, Gardner, PLB 643, 2006]
[Brodsky, BP, Yuan, Xiao, PLB 667, 2010