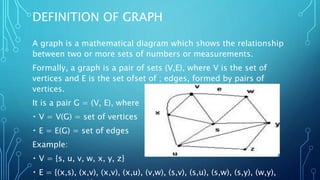
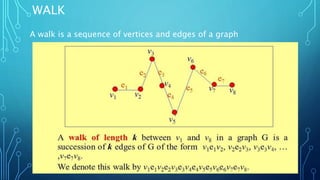
This presentation summarizes key concepts about graphs. It defines a graph as a pair of sets (V,E) where V is the set of vertices and E is the set of edges. It discusses types of graphs like simple graphs and connected graphs. It also defines important graph concepts such as subgraphs, walks, Euler paths and circuits, and shortest path problems. The presentation was delivered to lecturers in the Computer Science department on the topic of graphs.

1. WELCOME TO OUR
PRESENTATION
PRESENTED BY:
NAME- MD.MINHAJUL-ABEDIN ID-171-15-
1386
NAME- MD.OLIDE HASAN ID-181-15-
1791
PRESENTATION TOPIC – GRAPHS
PRESENTED TO: FARIA
NISHAT KHAN
LECTURER, DEPARTMENT OF CSE

2. CONTENT-
• Definition of Graph
• Some important points
• Types of graphs
• Walk
• Euler path & circuit
• Shortest Path Problems

3. DEFINITION OF GRAPH
A graph is a mathematical diagram which shows the relationship
between two or more sets of numbers or measurements.
Formally, a graph is a pair of sets (V,E), where V is the set of
vertices and E is the set ofset of ; edges, formed by pairs of
vertices.
It is a pair G = (V, E), where
V = V(G) = set of vertices
E = E(G) = set of edges
Example:
V = {s, u, v, w, x, y, z}
E = {(x,s), (x,v), (x,v), (x,u), (v,w), (s,v), (s,u), (s,w), (s,y), (w,y),

4. SOME IMPORTANT POINTS
• Loop and Multiple Edges
A loop is an edge whose endpoints are equal i.e., an edge joining
a vertex to it self is called a loop. We say that the graph has
multiple edges if in the graph two or more edges joining the
same pair of vertices.

5. TYPES OF GRAPH
• Simple Graph
A graph with no loops or multiple edges is called a simple graph.
We specify a simple graph by its set of vertices and set of edges,
treating the edge set as a set of unordered pairs of vertices and
write e = uv (or e = vu) for an edge e with endpoints u and v.
• Connected Graph
A graph that is in one piece is said to be connected,
whereas one which splits into several pieces is
disconnected.

6. SUBGRAPH
A graph all of whose points and lines are contained in a larger
graph.
Let G be a graph with vertex set V(G) and edge-list E(G). A
subgraph of G is a graph all of whose vertices belong to V(G) and
all of whose edges belong to E(G). For example, if G is the
connected graph below: • w, z} and E(G) = (uv, uw, vv, vw, wz,
wz} then the following graphs are

7. WALK
A walk is a sequence of vertices and edges of a graph

8. EULER PATH & CIRCUIT-
Euler Path is a path in the graph that passes each edge only
once. Euler Circut is a path in the graph that passes each edge
only once and return back to its original position. From Denition,
Euler Circuit is a subset of Euler Path

9. SHORTEST PATH PROBLEMS
• Directed weighted graph.
• Path length is sum of weights of edges on path.
• The vertex at which the path begins is the source vertex.
• The vertex at which the path ends is the destination vertex.

10. EXAMPLE

11. THANK YOU MA’AM