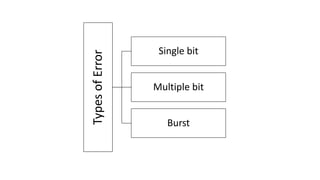
The document discusses error detection and correction methods essential for reliable data transmission, focusing on mechanisms like parity check, cyclic redundancy check, checksum, and Hamming code. It explains how each method identifies transmission errors and includes examples to illustrate their application. The goal is to ensure data integrity during transmission by detecting and correcting errors that may occur.