1. Laminating the core breaks up the conductive material into thinner sheets separated by insulating material. This increases the resistance to eddy currents by forcing them to travel longer, more tortuous paths through the laminations. 2. Cutting teeth into the core reduces the cross-sectional area available for eddy currents to flow. With a smaller area, less current can flow and induce smaller magnetic fields, resulting in lower losses. 3. Both techniques reduce eddy current losses by making it more difficult for currents to flow through the conductive material in closed loops in response to changing magnetic fields. This is done by either increasing the resistance and path

1. Magnetic Effect of a current-carrying conductor
Magnetic
Effect of a
current-
carrying
conductor
Electric and
magnetic
fields occur
naturally wherever
there is electricity.
Electric fields are
produced by electrically
charged objects.
Magnetic fields are
produced by magnets
and by an electric current in a wire. The magnetic field produced by an electric
current is put to practical use like electromagnets.
An electromagnet can be made by sending an electric current through a coil of
wire wound around an iron core, the coil usually consists of several hundred
turns of insulated copper wire.
When a current flows through the coil, it produces a magnetic field. If an iron core
is placed inside the coil, a stronger magnetic field will be created.

2. The soft iron core becomes temporarily magnetized when the current is switched
on. If loses its magnetism when the current is switched off. This effect is used in
electric bells and buzzers, and in scrapyards for shifting metal scraps around.
Magnetic Field Pattern
A magnetic field can be represented by lines that show the shape of the field.
Magnetic field lines which are close together represent a strong field. The field
direction is defined as the direction indicated by a compass needle placed in the
magnetic field.
A simple rule that can be used to determine the direction of the magnetic field
around a current-carrying wire is the “right-hand grip rule”. With the thumb of a
clenched right hand pointing in the direction of the conventional current, then the
fingers indicate the direction of the magnetic field.
The right-hand grip rule can also be used to indicate the direction of the magnetic
field around a coil. The right-hand grip rule for a solenoid, in this case, the thumb
points towards the north pole of the magnetic field while the fingers indicate the
direction of the current in the solenoid.
(The poles of a solenoid can also be determined by using the direction of current
as seen from each end. South = current flows clockwise in the solenoid. North =
current flows anticlockwise)

3. Magnetic Field Strength
A magnetic field exists whenever a current is present. When an electrical
appliance is switched on, there is a magnetic field around it. The field strength
increases with current. Thus, a stronger magnetic field exists near appliances
which use a bigger current. However, the strength of the magnetic field
decreases with distance from a current-carrying source.
Electric fields are shielded by most objects, such as walls, buildings and trees but
magnetic fields are not. In spite of being buried in the ground, magnetic fields of
power lines are still not eliminated.
Answer for number 1, 2, 3
1. Magnets attract objects of iron, cobalt and nickel.
2. The force of attraction of a magnet is greater at its poles than in the middle.
3. Like poles of two magnets repel each other.
4. Opposite poles of two magnets attracts each other.
5. If a bar magnet is suspended by a thread and if it is free to rotate, its South
Pole will move towards the North Pole of the earth and vice versa.
CHARACTERISTICS
OF MAGNETIC LINES
OF FORCE
1. Magnetic lines of force start from the North Pole and end at the South Pole.
2. They are continuos through the body of magnet
3. Magnetic lines of force can pass through iron more easily than air.
4. Two magnetic lines of force can not intersect each other.
5. They tend to contract longitudinally.
6. They tend to expand laterally.
For latest information , free computer courses and high impact notes visit :
www.citycollegiate.com

4. FERROMAGNETIC
SUBSTANCES
Substances that behave like a magnet in the presence of a magnetic field are
known as FerromagneticSubstances.
EXAMPLES: Iron, cobalt and nickel are ferromagnetic substances.
SOLENOID
Solenoid is a coil of wire. Solenoid is a coil wound on a cylindrical frame of iron or
any material when an electric current passes through the Solenoid, a magnetic
field is produced around it. It has suitable numbers of turns of wire.
Magnetic field of solenoids is given by
B = µonI
Magnetic field inside the solenoid is very strong and uniform but it is very weak
outside the solenoid.
Answer 5
When an electrical wire is exposed to a magnet, the current in that wire will be
affected by a magnetic field. The effect comes in the form of a force. The
expression for magnetic force on current can be found by summing the magnetic
force on each of the many individual charges that comprise the current. Since
they all run in the same direction, the forces can be added.
The force (F) a magnetic field (B) exerts on an individual charge (q) traveling at
drift§velocity§ vd is:
F=qvdBsinθ

5. In this instance, θ represents the angle between the magnetic field and the wire
(magnetic force is typically calculated as a cross product). If B is constant
throughout a wire, and is 0 elsewhere, then for a wire with N charge carriers in its
total length l, the total magnetic force on the wire is:
F=NqvdBsinθ.
Given that N=nV, where n is the number of charge carriers per unit volume and V
is volume of the wire, and that this volume is calculated as the product of the
circular cross-sectional area A and length (V=Al), yields the equation§:
F=(nqAvd)lBsinθ.
The terms in parentheses are equal to current (I), and thus the equation can be
rewritten as:
F=IlBsinθ
The direction of the magnetic force can be determined using the right hand rule,
demonstrated in . The thumb is pointing in the direction of the current, with the
four other fingers parallel§ to the magnetic field. Curling the fingers reveals the
direction of magnetic force.

6. Right Hand Rule
Source: Boundless. “Magnetic Force on a Current-Carrying Conductor.”
Boundless Physics. Boundless, 21 Jul. 2015. Retrieved 05 Oct. 2015 from
https://www.boundless.com/physics/textbooks/boundless-physics-
textbook/magnetism-21/magnetic-fields-magnetic-forces-and-conductors-
159/magnetic-force-on-a-current-carrying-conductor-560-2459/
Answer 6

8. Magnetic Hysteresis
Table of Contents
1 Introduction§
2 Hysteresis Loop Structure§
3 Variations of Hysteresis Loops§
4 Importance of Hysteresis Loops§
5 Questions§
6 Answers§
7 Additional Links§
8 References§
9 Contributors §
A magnetic hysteresis, otherwise known as a hysteresis loop, is a representation
of the magnetizing force (H) versus the magnetic flux density (B) of a
ferromagnetic material. The curvature of the hysteresis is characteristic of the
type of material being observed and can vary in size and shape (i.e. narrow or
wide). The loop can be generated by using a Hall Effect sensor to measure the
amount of magnetic field at various points - when in the presence of a magnetic
field, when it is removed from the magnetic field, and when a force is applied to
bring the magnetic flux back to zero. These loops are important in the memory
capacity of devices for audio recording or magnetic storage of data on computer
disks.
Introduction
Hysteresis loops are generated from the
observation of ferromagnetic materials.
Ferromagnetic materials are the most
common of the five classes of magnetic materials: diamagnetic, paramagnetic,
ferrimagnetic§, ferromagnetic, and antiferromagnetic§. Without a magnetic field,

9. ferromagnetic materials exhibit paramagnetic behavior wherein their magnetic
dipole moments§ are random and disordered as seen in Figure 1a. Once a
ferromagnetic material is introduced to a magnetic field, however, their dipole
moments align parallel and in the same direction resulting in a much stronger
magnetic field (Figure 1b). These dipole moments are so highly ordered that
when removed from the magnetic field, there is still some remnant magnetization.
In order to reduce the magnetic flux back to zero, a coercive force must be
applied wherein the dipole moments cancel each other out. This hysteresis loop
therefore summarizes the pathway that a ferromagnetic material takes from the
addition and removal of a magnetizing force.
Hysteresis Loop Structure
Hysteresis loops begin at a starting point (H=0) wherein its magnetic dipole
moments are disoriented and the material portrays paramagnetism. When a
magnetizing force (H) is adding to the material, it follows the pathway up to the
saturation point (+Hs). At this point all the magnetic dipole moments are aligned

10. in the direction of the magnetizing force and the magnetic flux no longer
increases. When H is reduced to zero, some remnant magnetization remains;
this point is known as the retentivity point (+Br). In order to remove this remnant
magnetization, a coercive magnetizing force is applied in the reverse direction.
The point in which there is no longer a magnetic flux (B=0) due to the cancelation
of dipole moments acting in opposite directions is known as the coercivity point (-
Hc). As the magnetizing force increases in the negative direction, the same
saturation occurs as it did before however in the opposite direction (-Hs). The
loop continues with an equal but opposite retentivity point (-Br) and coercivity
point (+Hc) until its original saturation point (+Hs). Figure 2 portrays this full cycle
hysteresis loop wherein points a and d are the +/- Hs, points b and e are the +/-
Br, and points c and f are the +/- Hc. The magnetic dipole spins at these
respective points can be seen in Figure 3 wherein the spins begin disoriented,
then align with the magnetic field, and finally misalign until the moments cancel
each other out to produce no net magnetic moment. Also notice that the curve
does not ever go back to the origin (B and H=0). In order to get back to this point,
the material will need to be demagnetized (i.e. return to having paramagnetic
behavior) by hitting the material against a surface, reversing the direction of the
magnetizing field, or heating it passed its Neel temperature. At this temperature,
a ferromagnetic material becomes paramagnetic due to thermal fluctuations in
the magnetic dipole moments that disorient the spins.
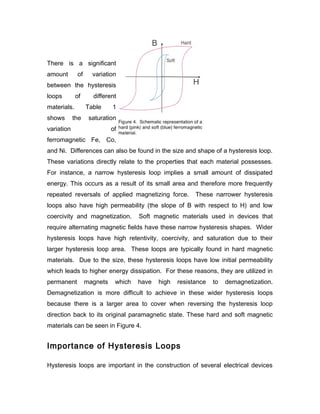
Variations of Hysteresis Loops
Table 1. Saturation point for ferromagnetic materials Fe, Co, and Ni at 0 K.
Metal Hs [A/m]
Fe 1.75 x 10
6
Co 1.45 x 10
6
Ni 0.51 x 10
6

11. There is a significant
amount of variation
between the hysteresis
loops of different
materials. Table 1
shows the saturation
variation of
ferromagnetic Fe, Co,
and Ni. Differences can also be found in the size and shape of a hysteresis loop.
These variations directly relate to the properties that each material possesses.
For instance, a narrow hysteresis loop implies a small amount of dissipated
energy. This occurs as a result of its small area and therefore more frequently
repeated reversals of applied magnetizing force. These narrower hysteresis
loops also have high permeability (the slope of B with respect to H) and low
coercivity and magnetization. Soft magnetic materials used in devices that
require alternating magnetic fields have these narrow hysteresis shapes. Wider
hysteresis loops have high retentivity, coercivity, and saturation due to their
larger hysteresis loop area. These loops are typically found in hard magnetic
materials. Due to the size, these hysteresis loops have low initial permeability
which leads to higher energy dissipation. For these reasons, they are utilized in
permanent magnets which have high resistance to demagnetization.
Demagnetization is more difficult to achieve in these wider hysteresis loops
because there is a larger area to cover when reversing the hysteresis loop
direction back to its original paramagnetic state. These hard and soft magnetic
materials can be seen in Figure 4.
Importance of Hysteresis Loops
Hysteresis loops are important in the construction of several electrical devices

12. that are subject to rapid magnetism reversals or require memory storage. Soft
magnetic materials (i.e. those with smaller and narrower hysteresis areas) and
their rapid magnetism reversals are useful in electrical machinery that require
minimal energy dissipation. Transformers and cores found in electric motors
benefit from these types of materials as there is less energy wasted in the form of
heat. Hard magnetic materials (i.e. loops with larger areas) have much higher
retentivity and coercivity. This results in higher remnant magnetization useful in
permanent magnets where demagnetization is difficult to achieve. Hard
magnetic materials are also useful in memory devices such as audio recording,
computer disk drives, and credit cards. The high coercivity found in these
materials ensure that memory is not easily erased.
Answer 7

13. Reducing Eddy current losses§
up
vote4down
votefavorite§
Eddy currents are setup in any metallic block which is in the vicinity
of changing magnetic fluxes. These primarily cause heat losses, and
in certain cases causes damping of the relative motion between the
metallic block (where the currents are induced) and the magnet
producing the field.To reduce these effects, we use two strategies:-
10 Laminating the metallic core, that is to be in the
vicinity of changing magnetic flux.
11 By drawing teeth along the piece of metal.
I fail to understand how these would reduce the eddy losses? The
reason cited in the first case§ is the eddy current path will be blocked by
the laminations§. But from what I see, laminations just make the eddy
currents go in smaller circles, and the path length traversed by the
eddy currents are actually more than in the case without laminations,
and therefore the resistance should increase, and the power losses
should increase!
In the second case§, the reason cited§ is the reduction in the area of
the eddy current loops and hence a smaller magnetic moment for
damping.($vec mu=Ivec A$)But again, although the area of each
eddy current loop has decreased, but then individual loops in
different "teeth" can produce individual moments, and the net area
being same, the net moment will still be equal producing similar
deacceleration!

14. Answer 8&9