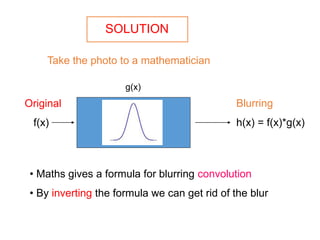
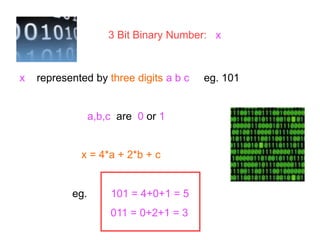
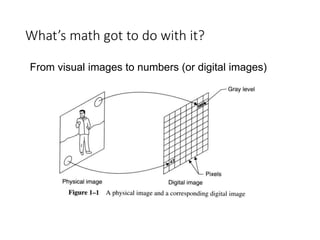
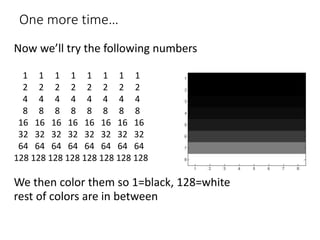
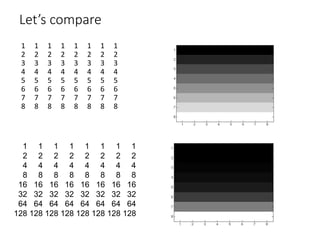
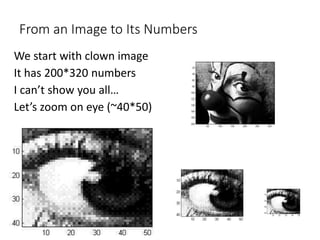
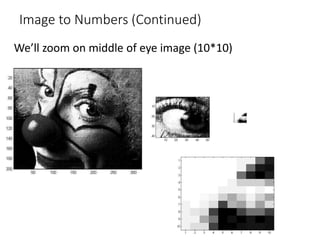
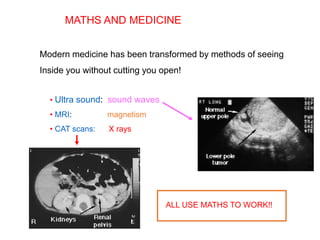
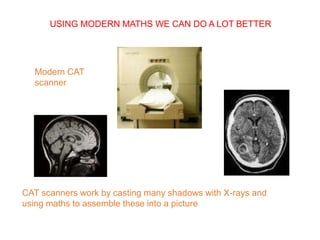
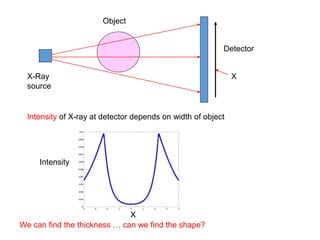
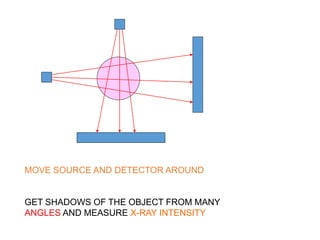
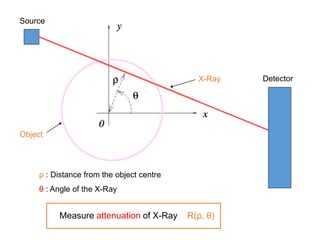
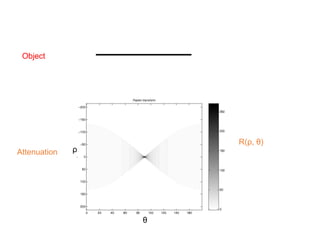
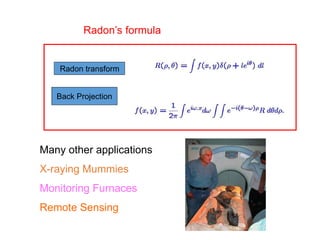
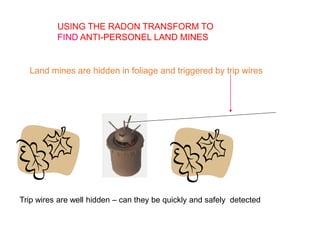
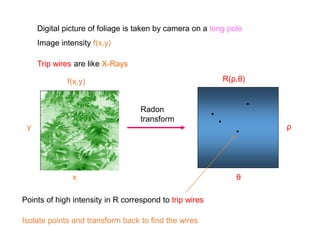
This document discusses the importance of mathematics in everyday life through several examples. It begins by addressing common misconceptions that mathematics is hard, boring, and irrelevant to real life. It then provides examples of how mathematics is used in crime detection, medicine, finding landmines, art, music, and predicting the future. The document goes on to discuss how the modern world would not exist without mathematics and provides scenarios of what life would be like without numbers. It then focuses on specific examples of how mathematics is used in crime detection using image processing techniques, medicine through medical imaging technologies like CAT scans and MRI, and finding hidden trip wires for landmines. It emphasizes that mathematics allows us to see inside the body and world without cutting them open