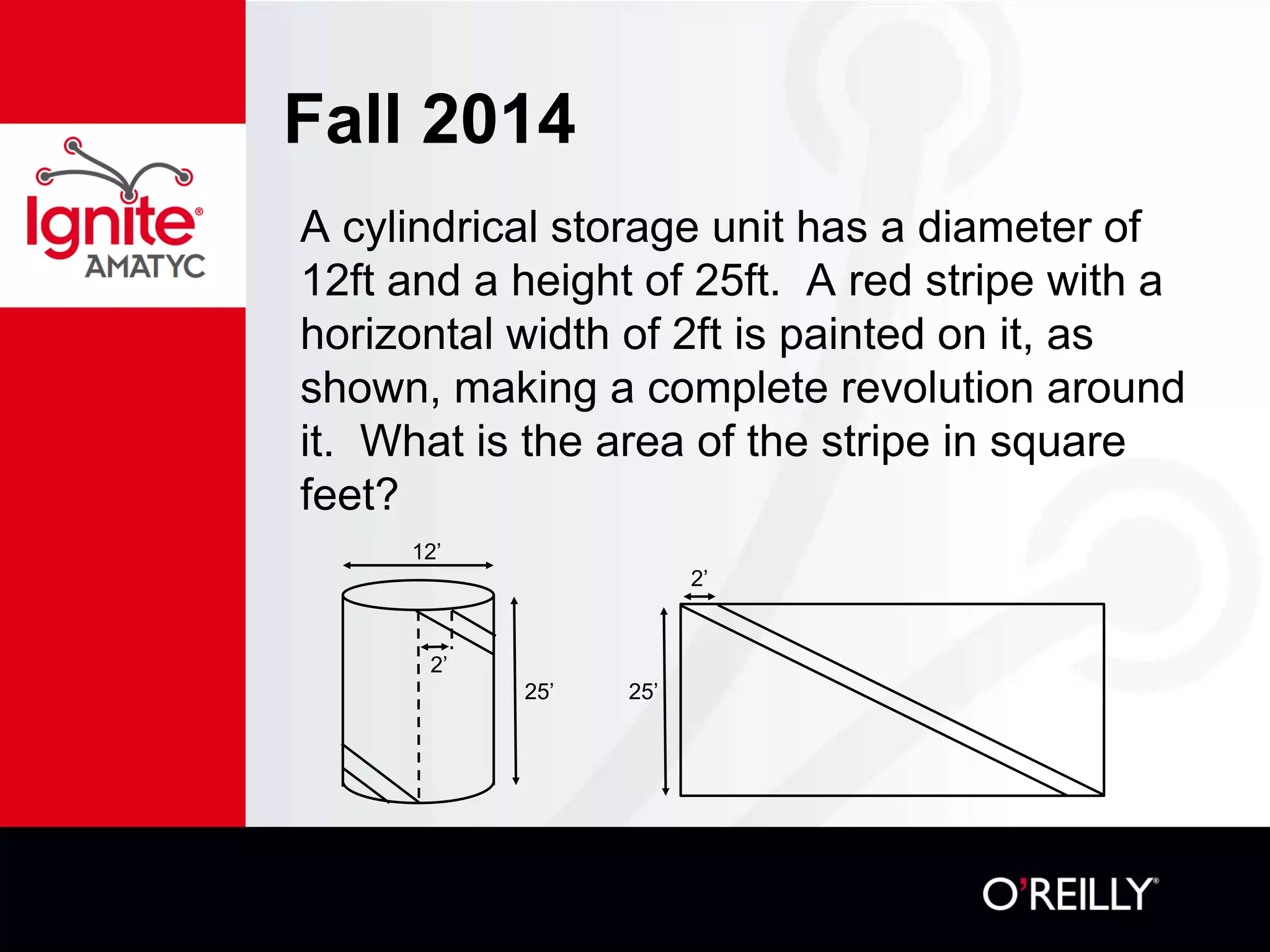
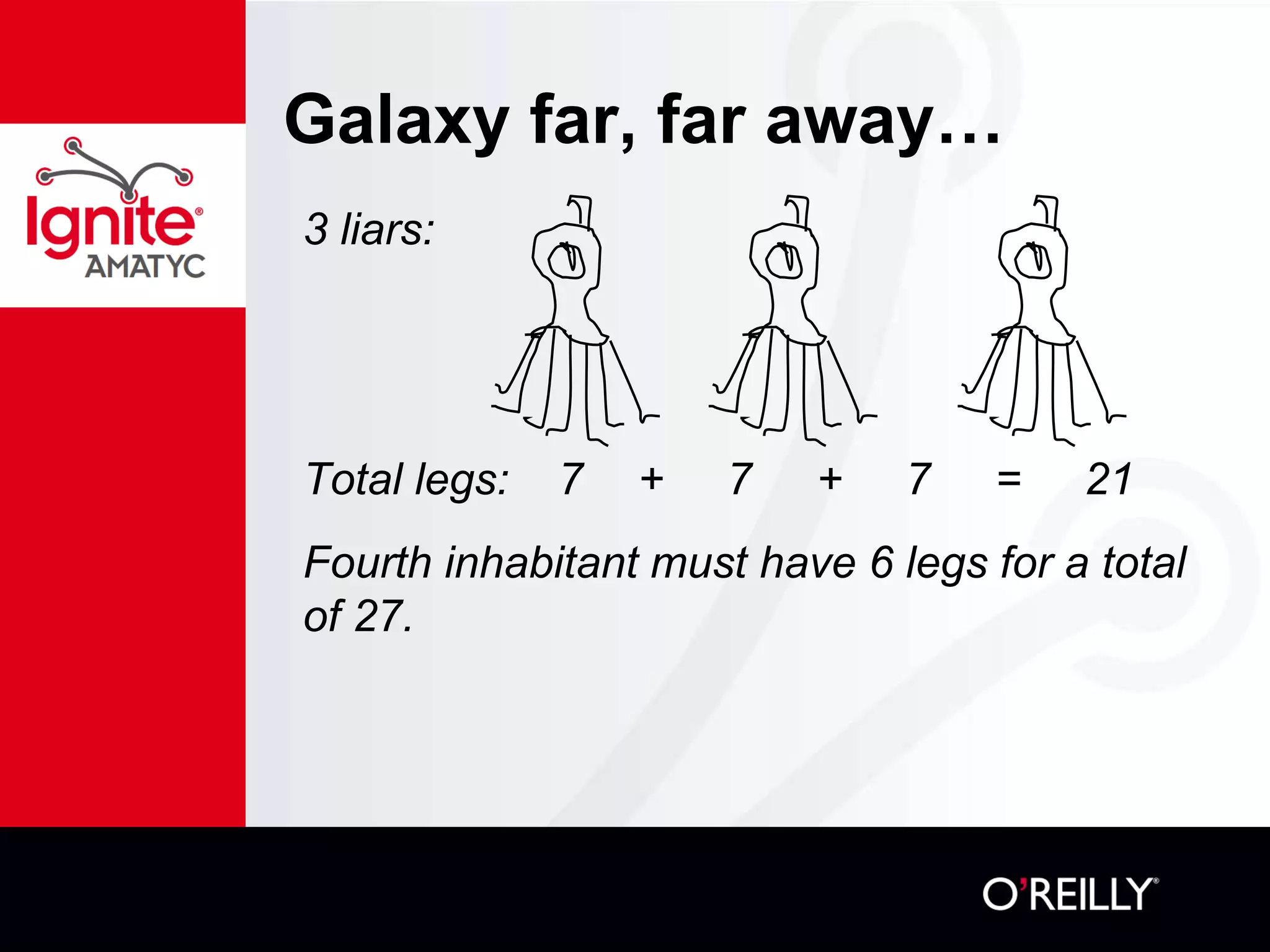
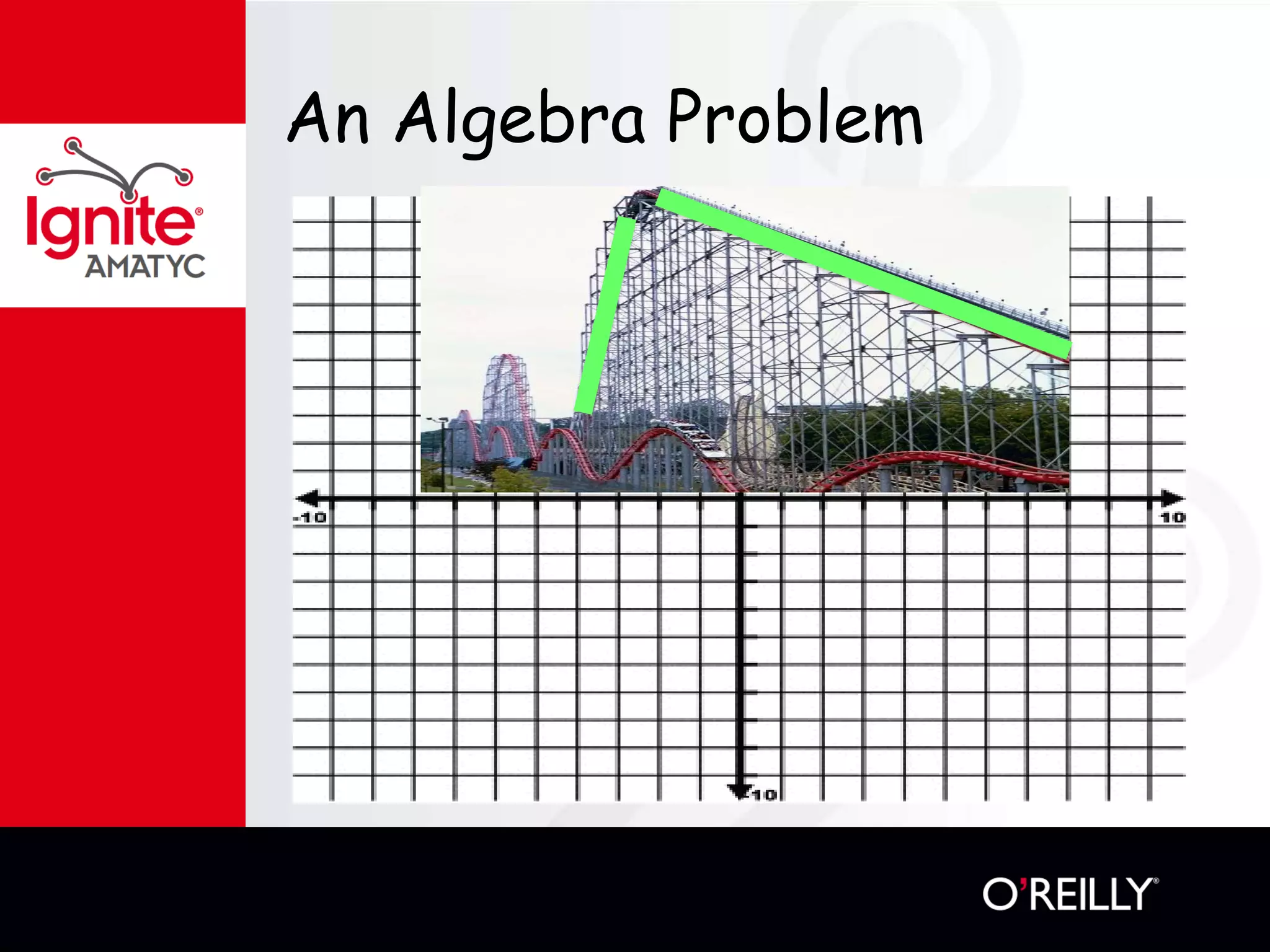
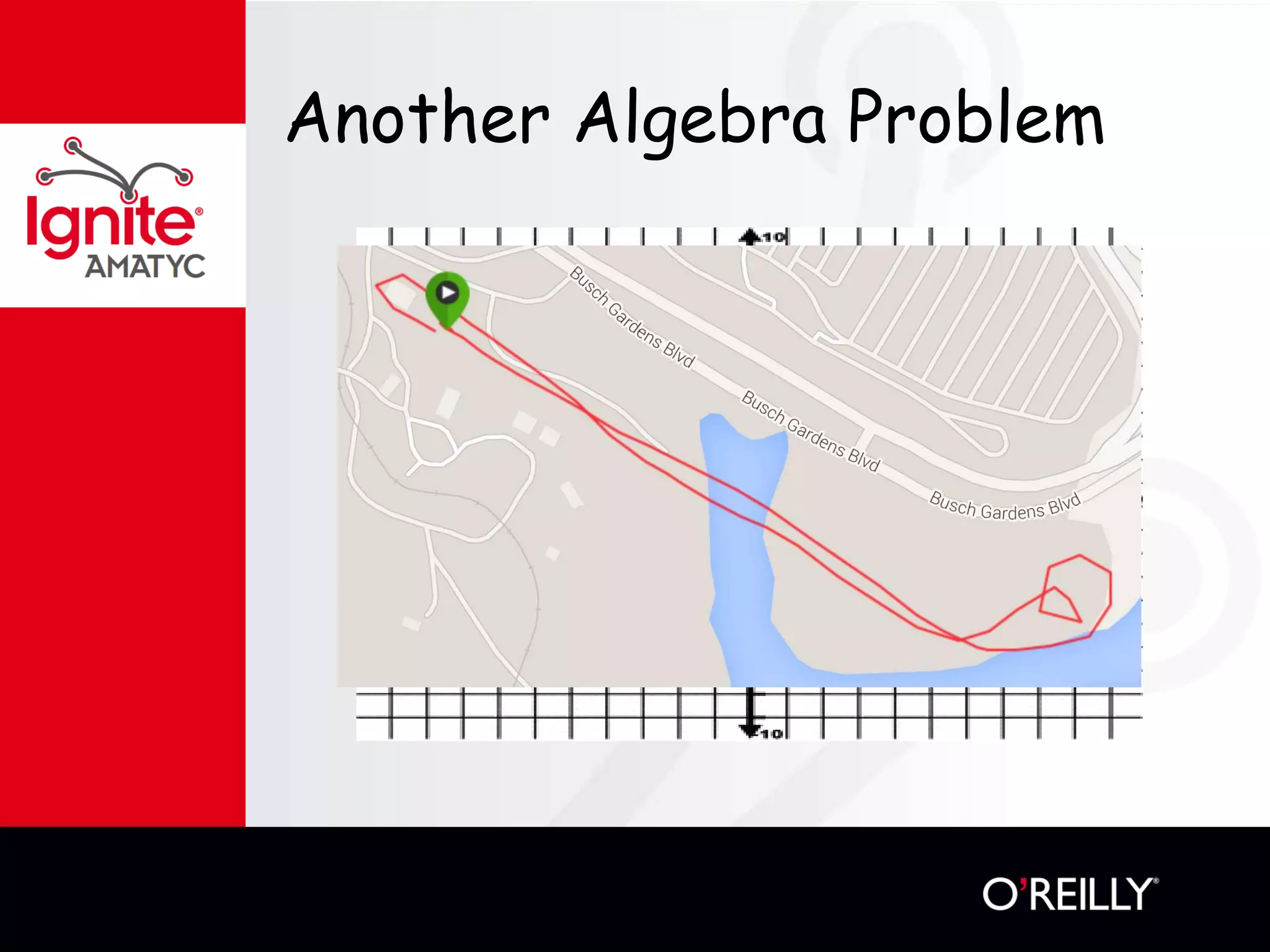
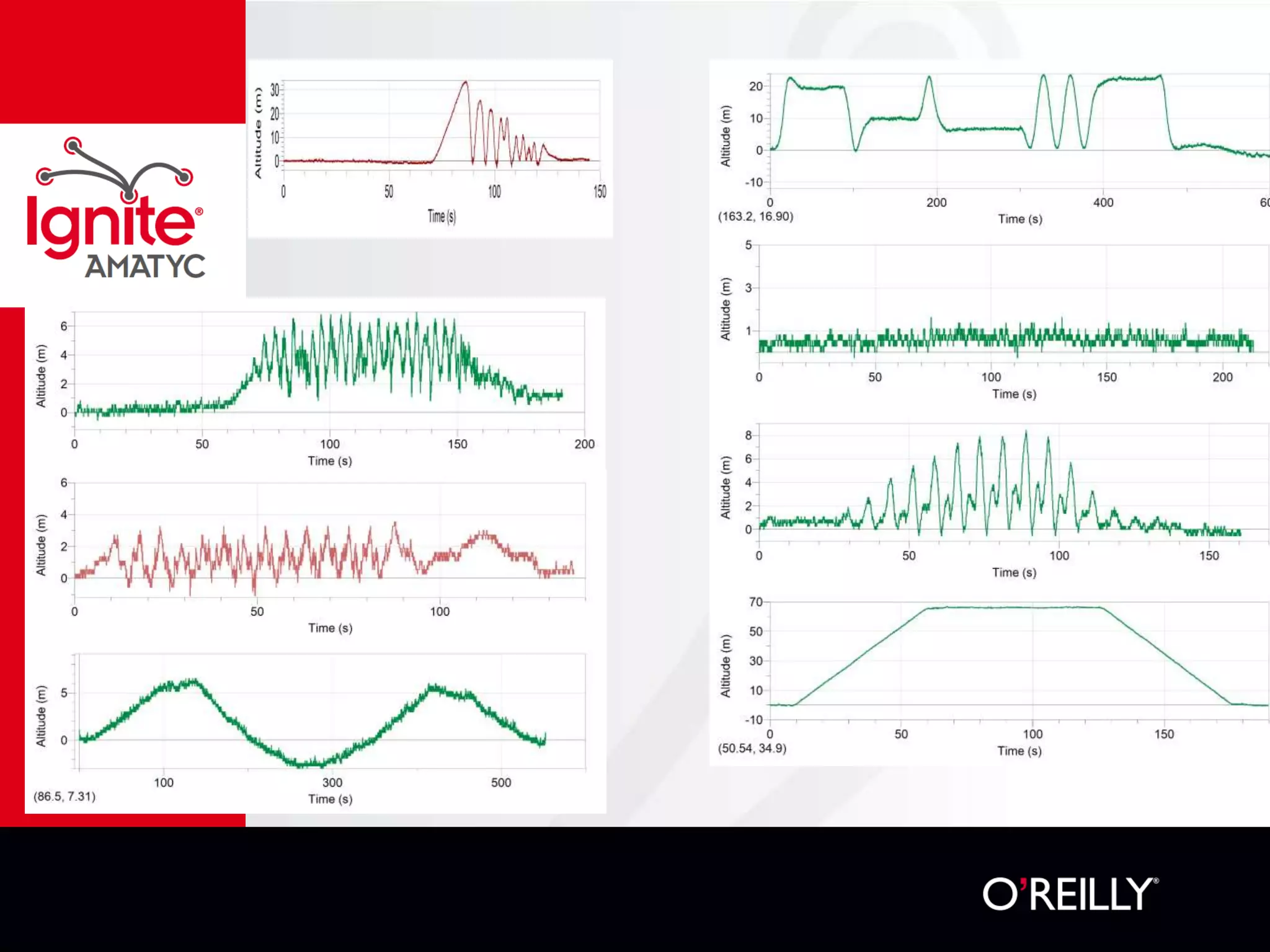
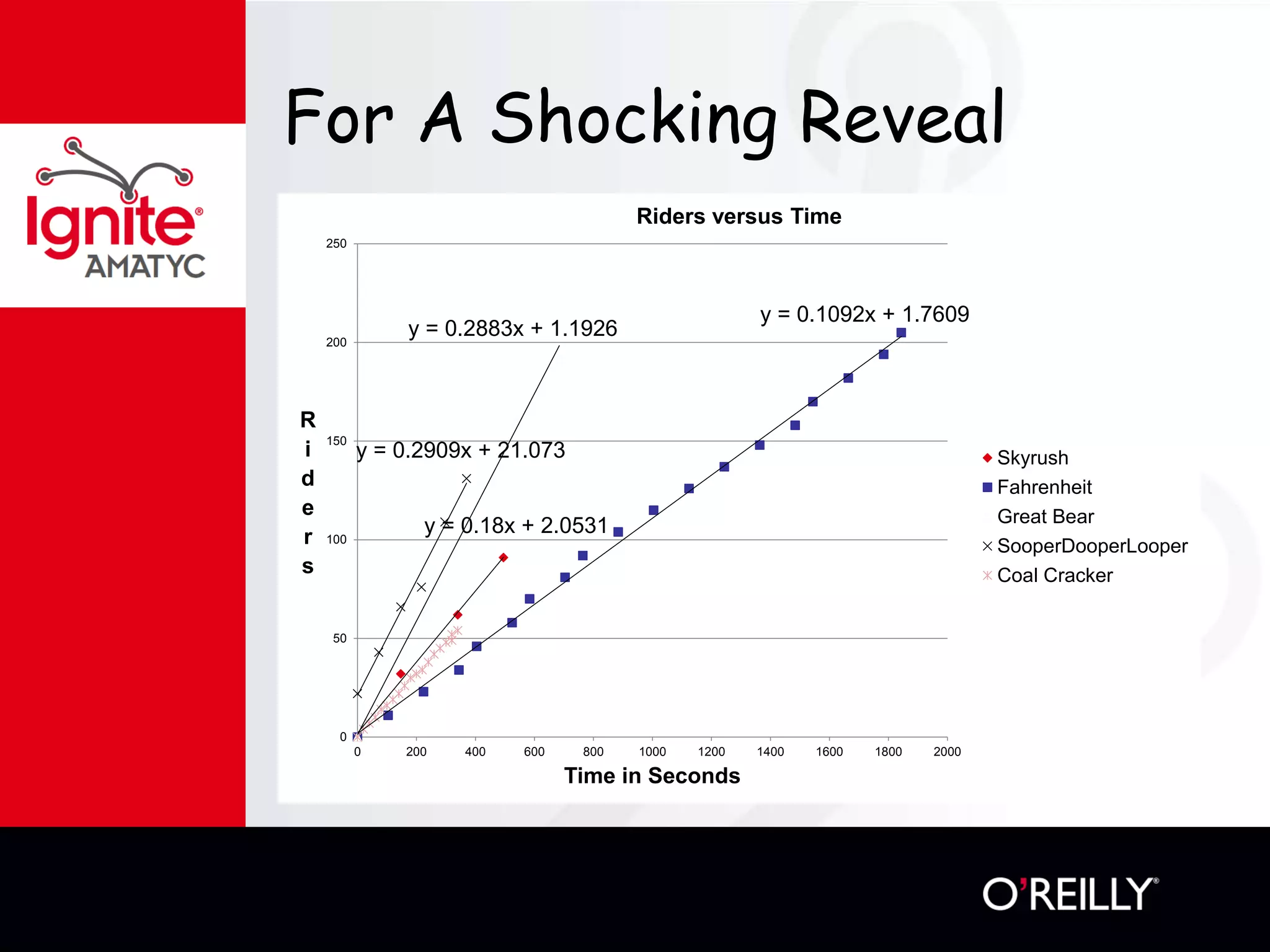
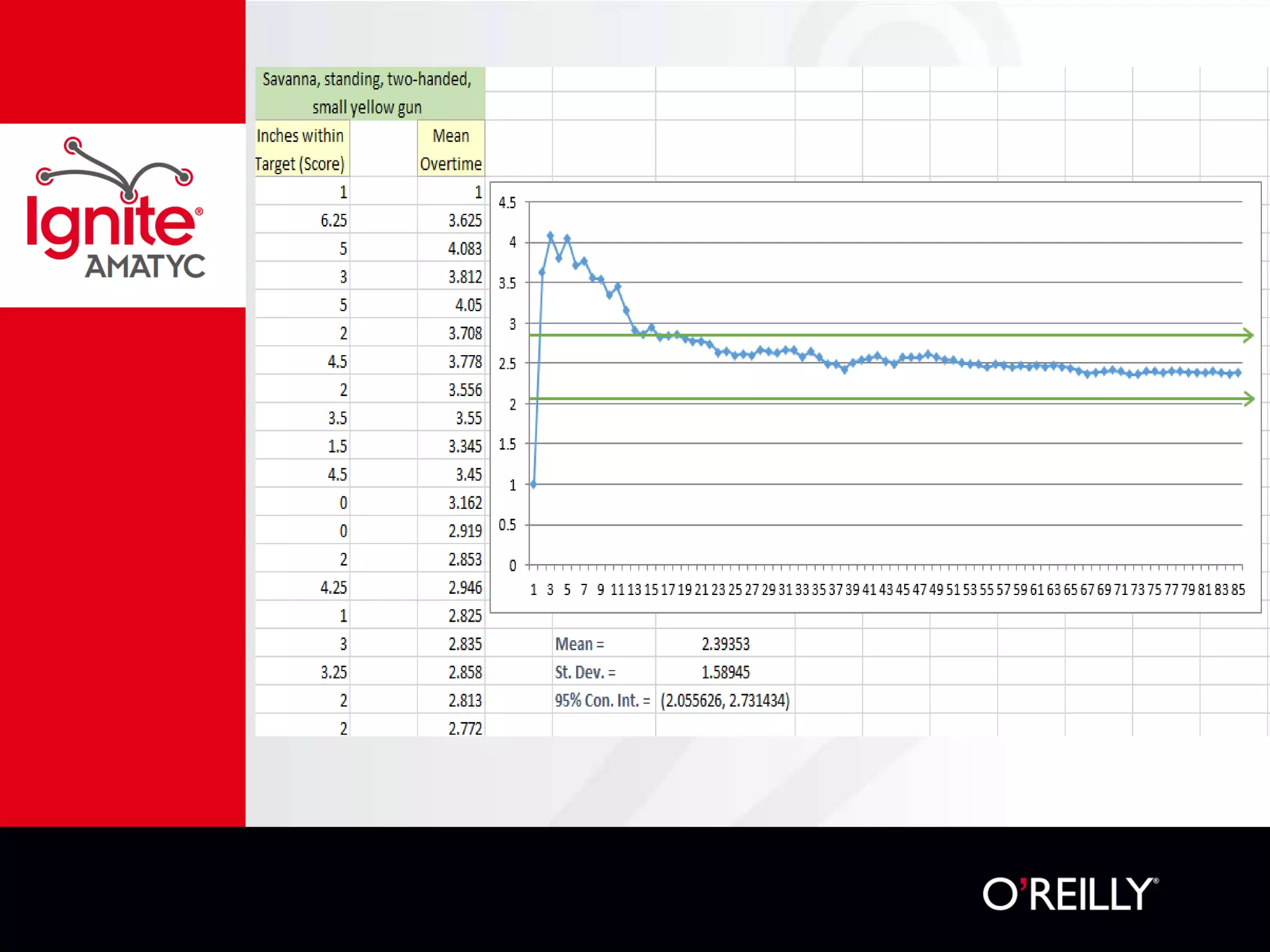
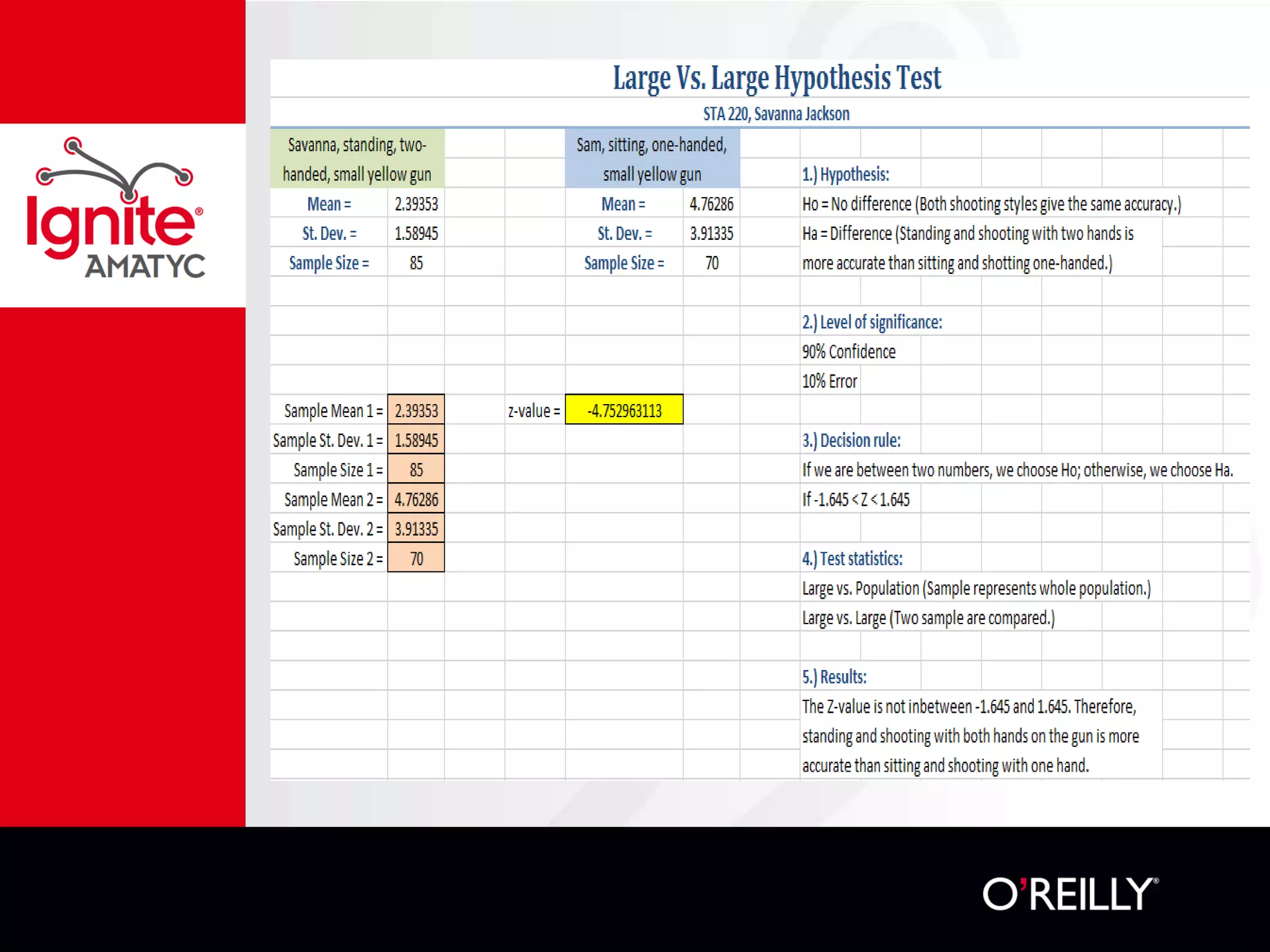
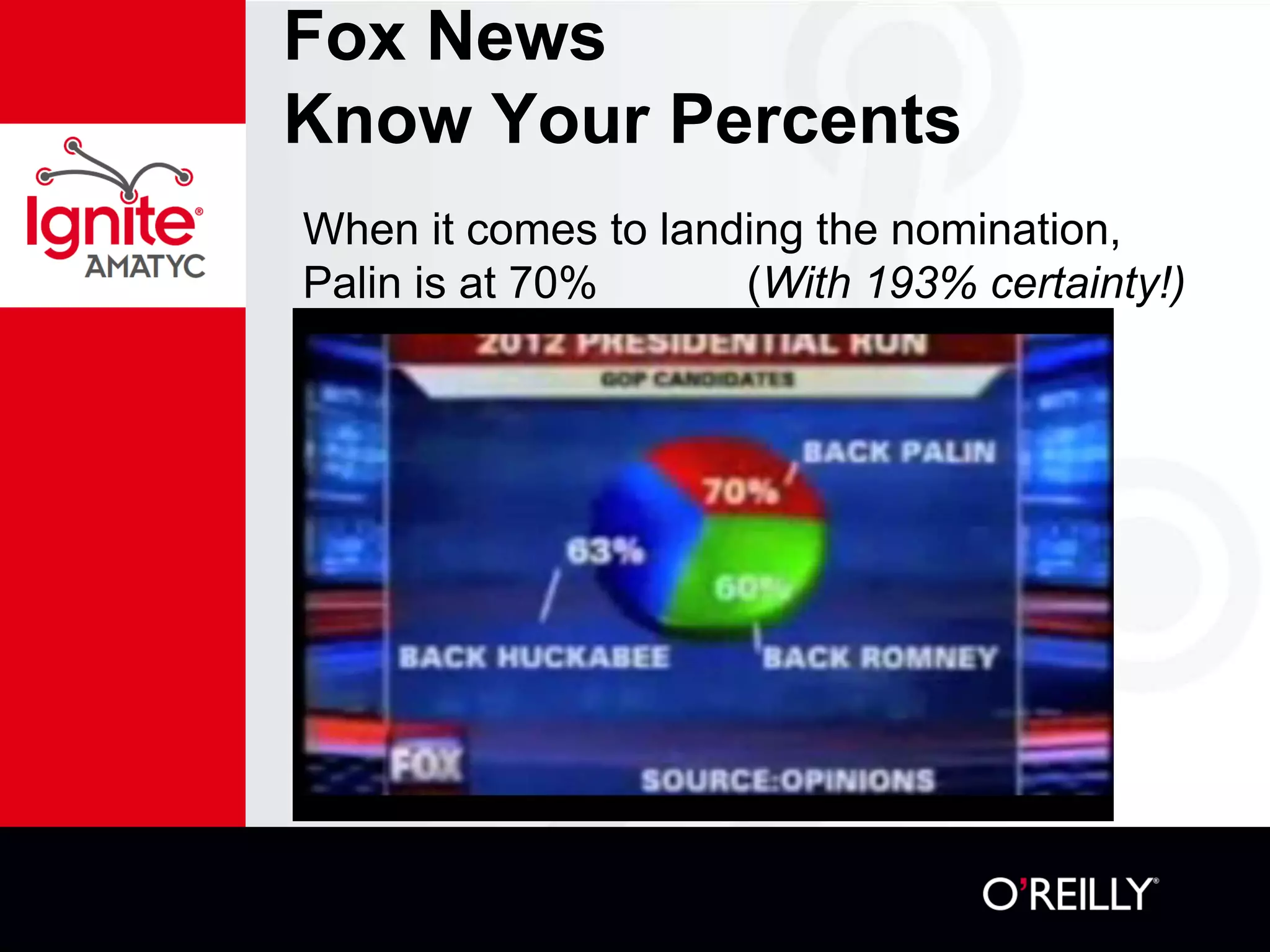
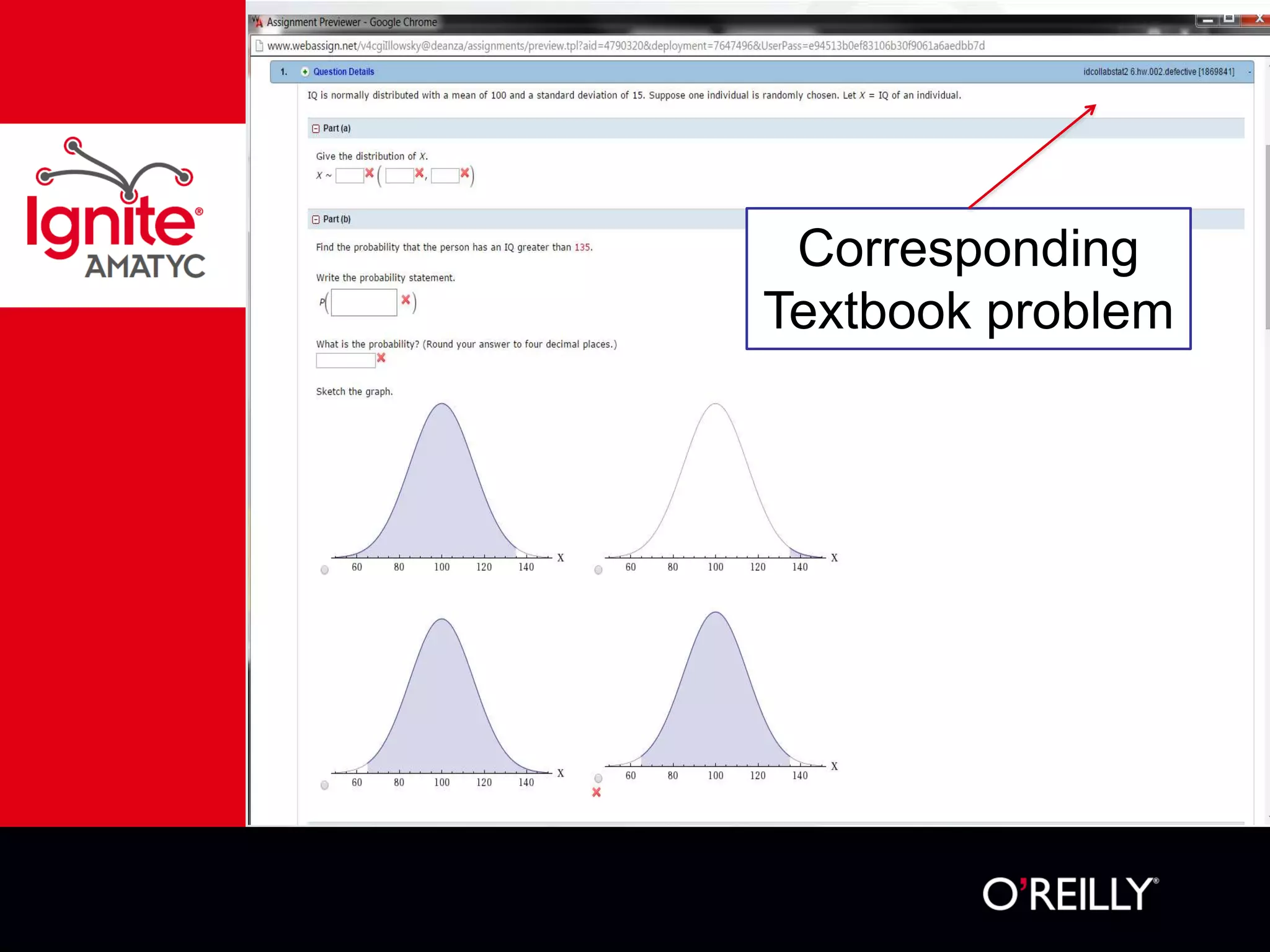
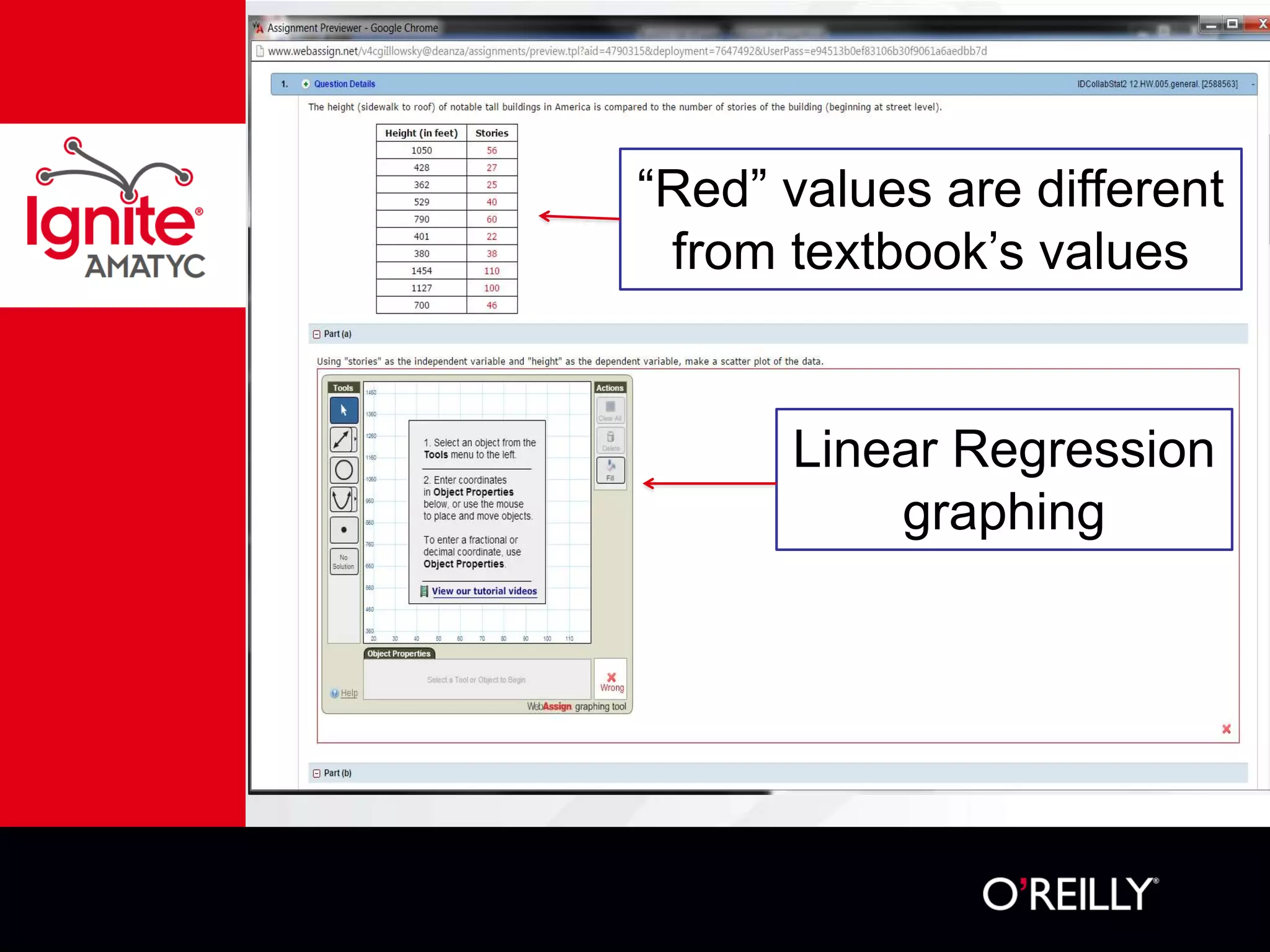
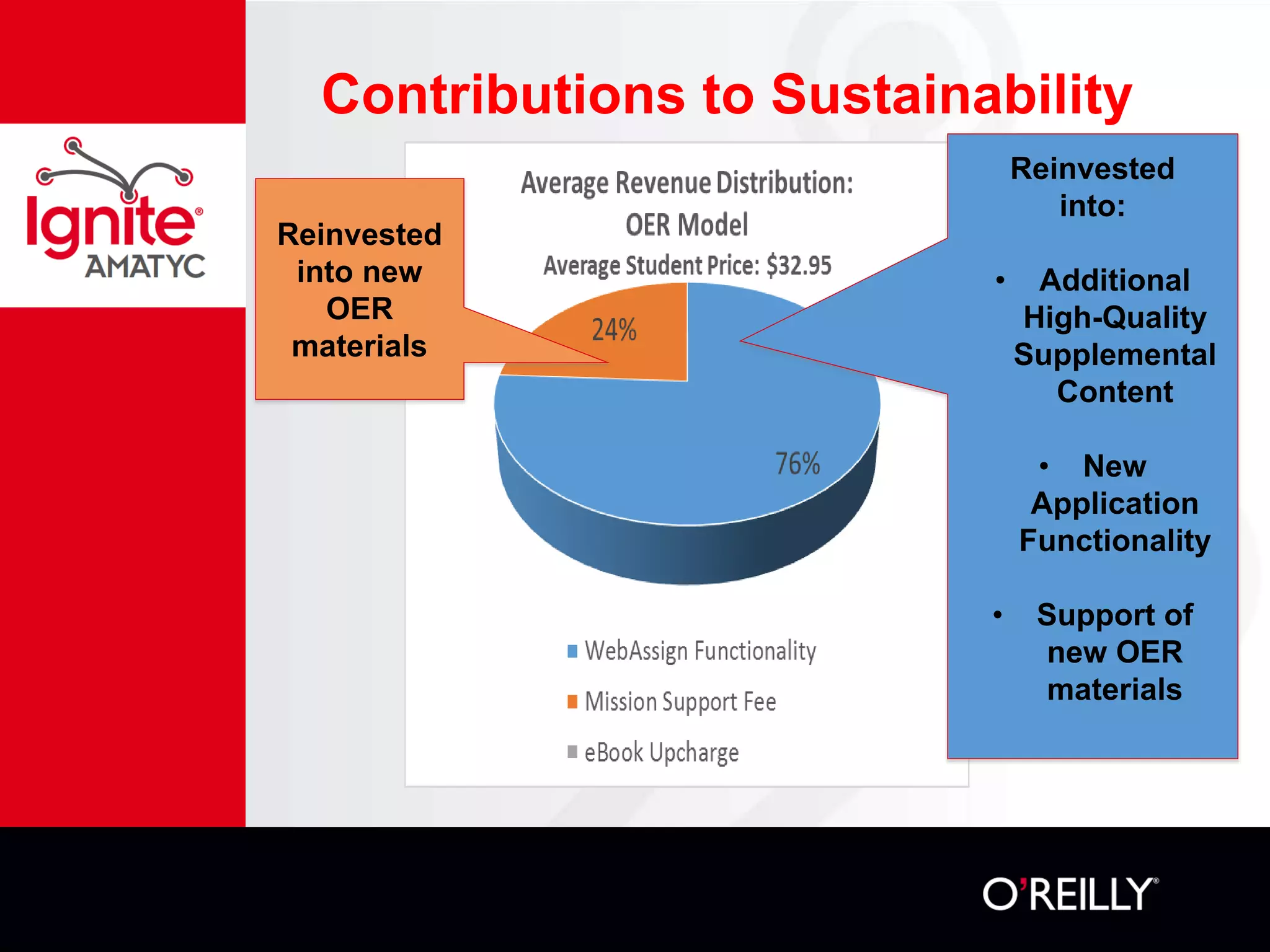
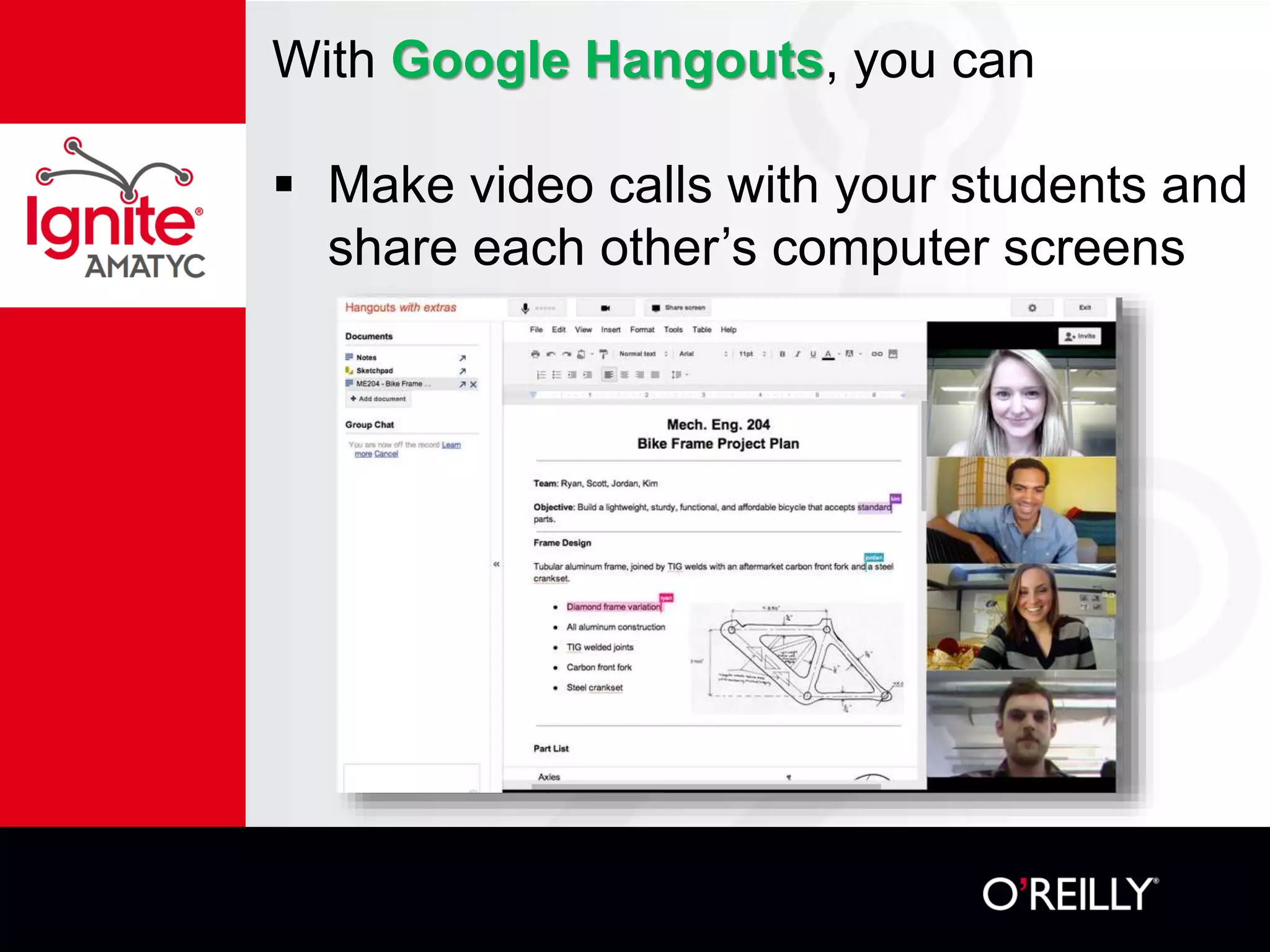
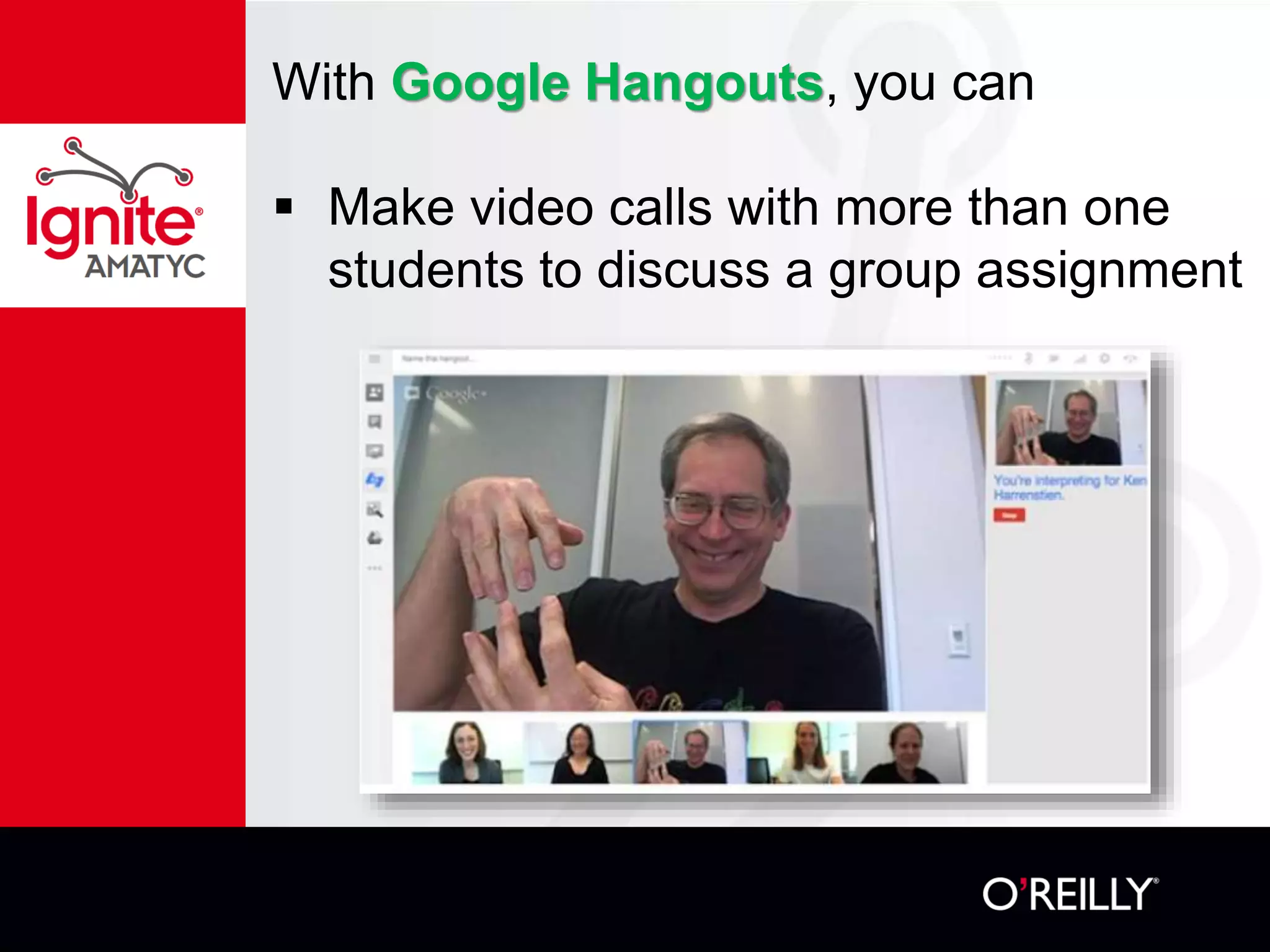
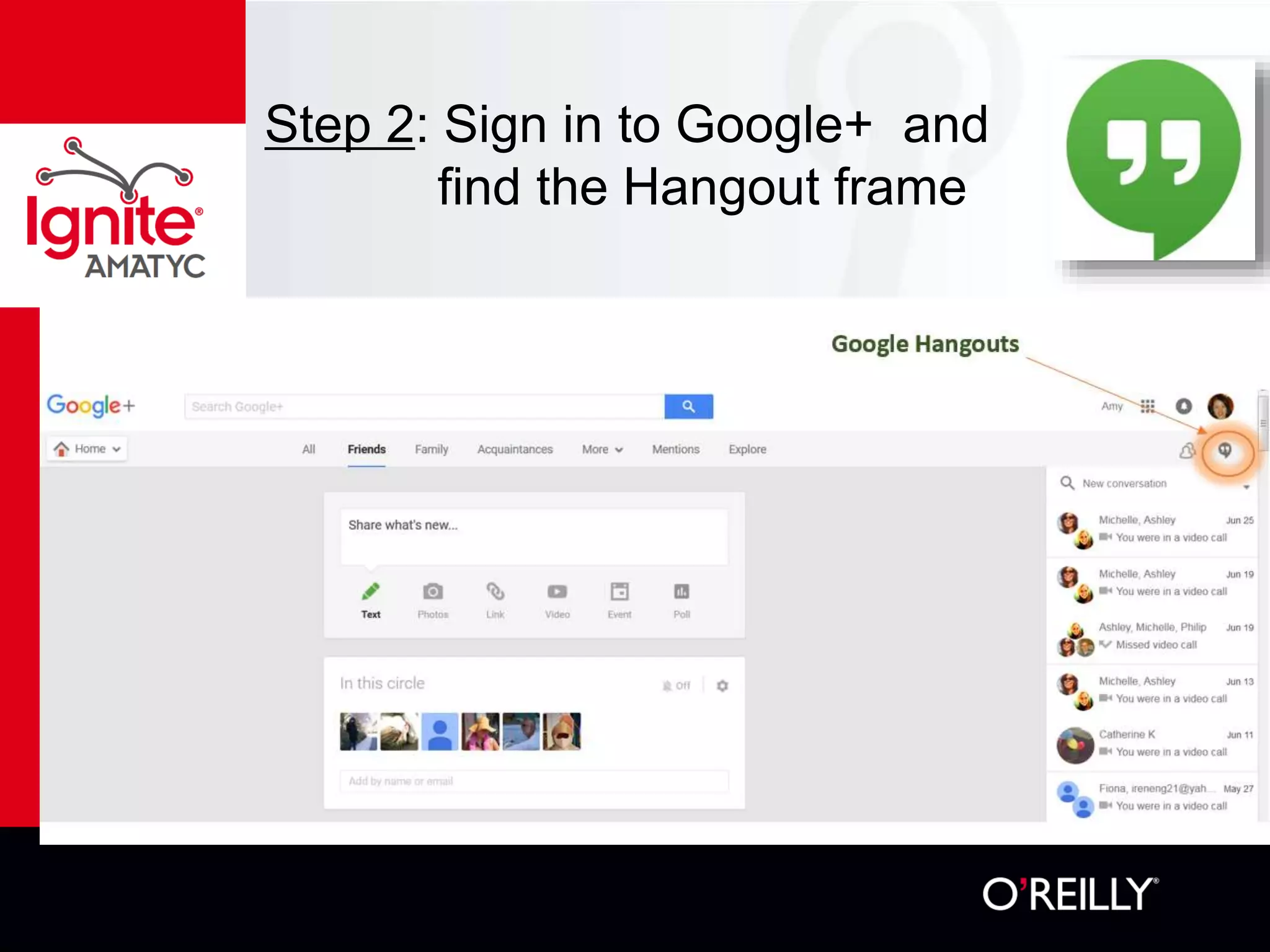
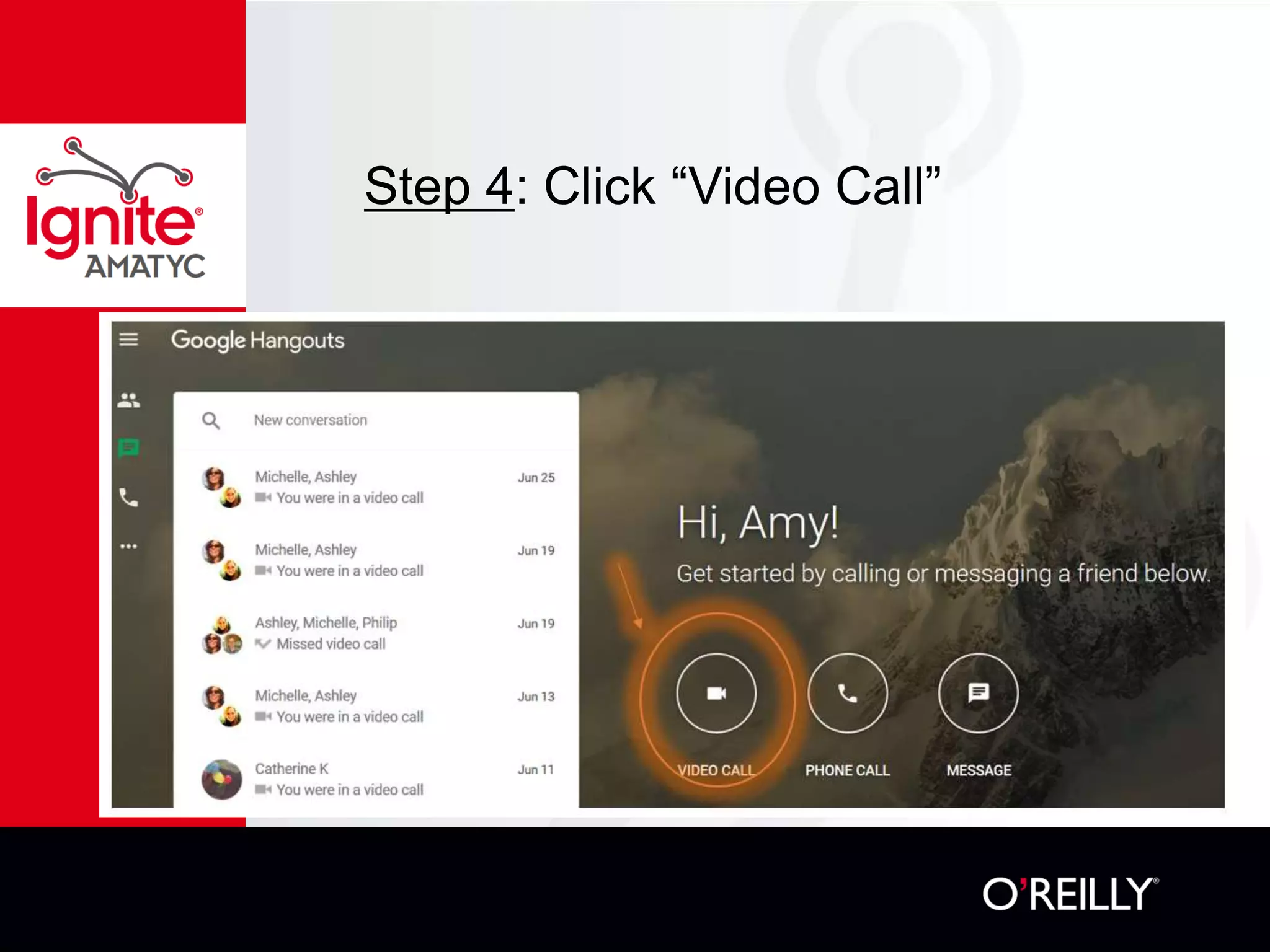
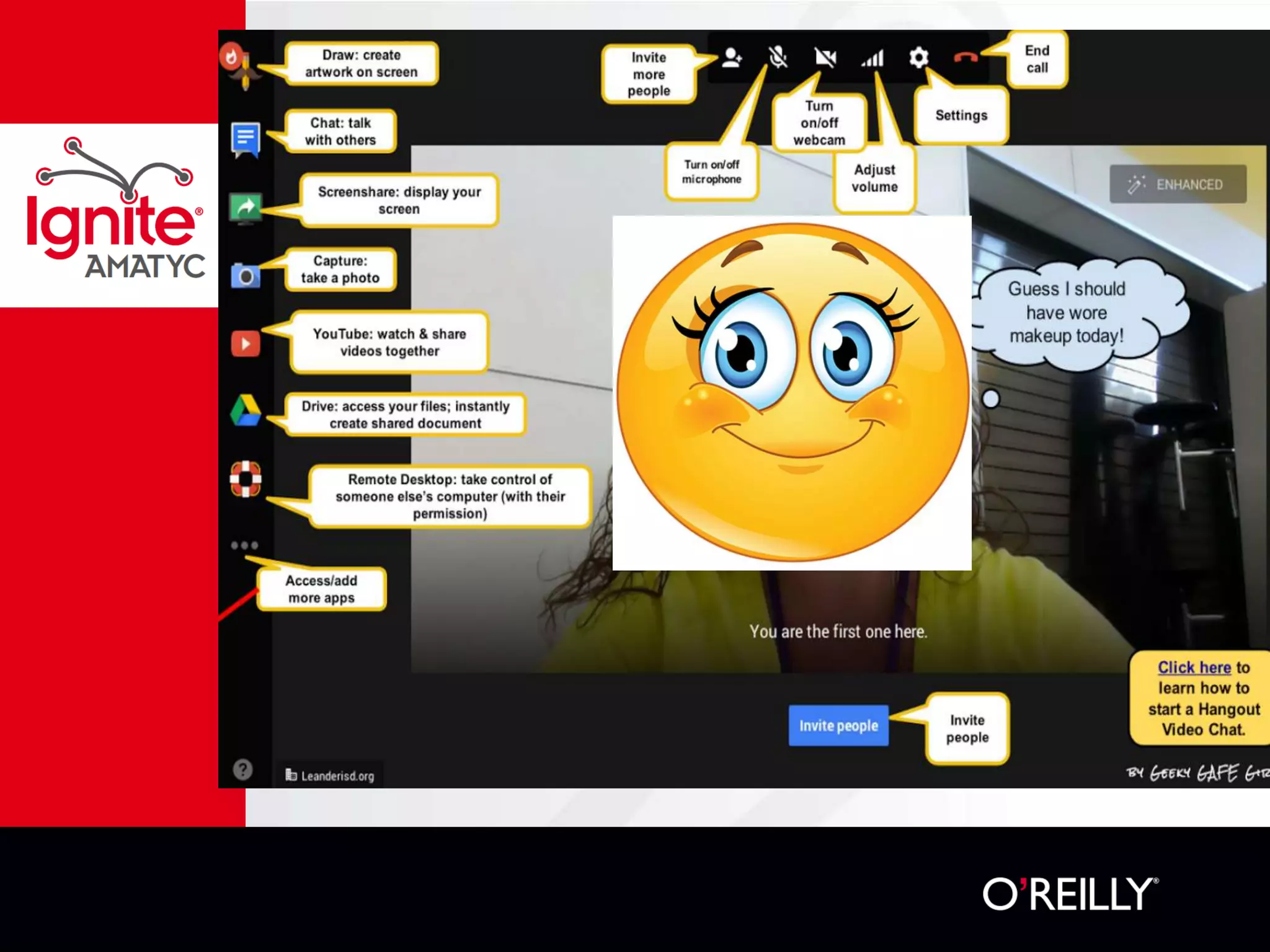
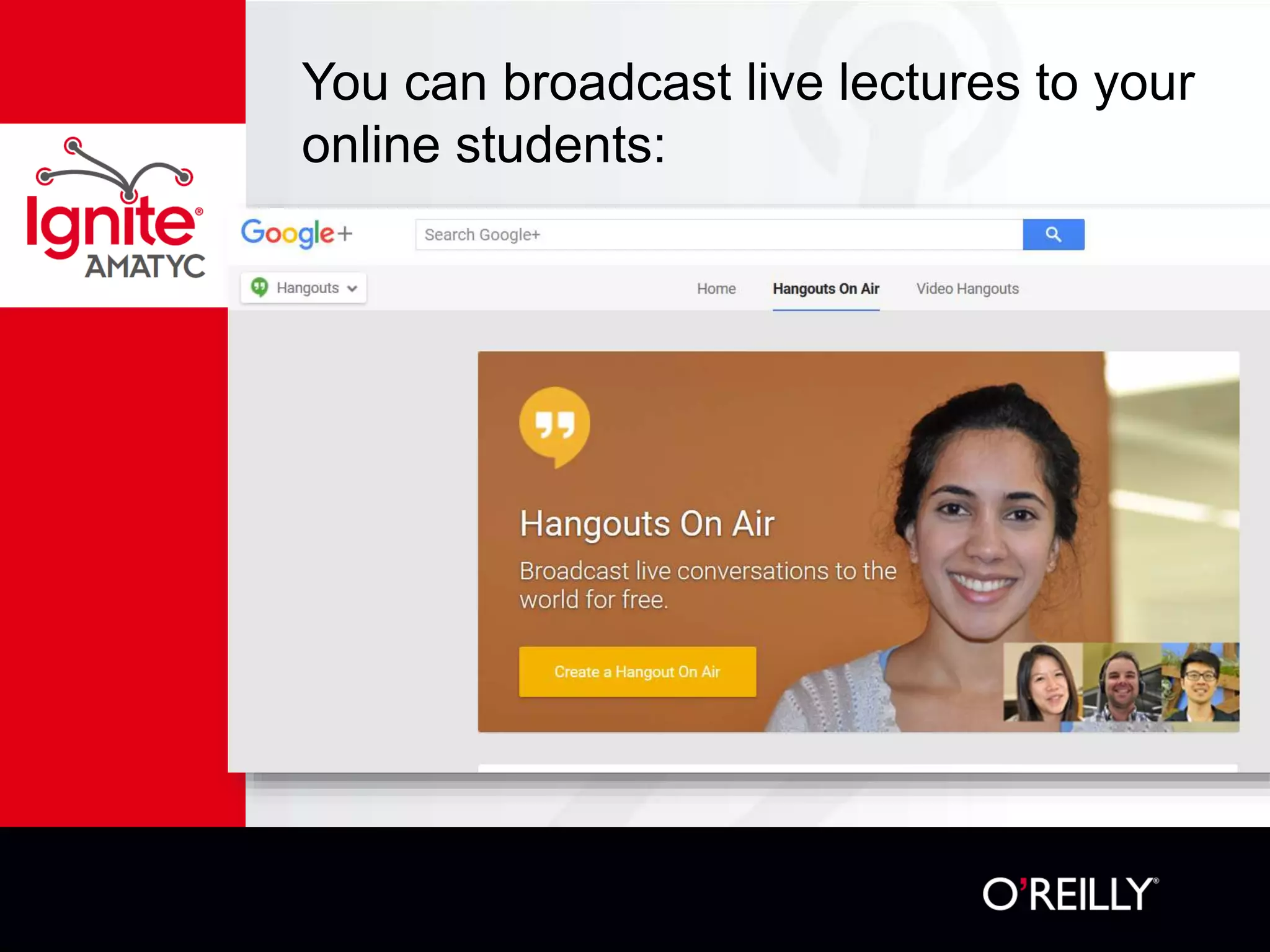
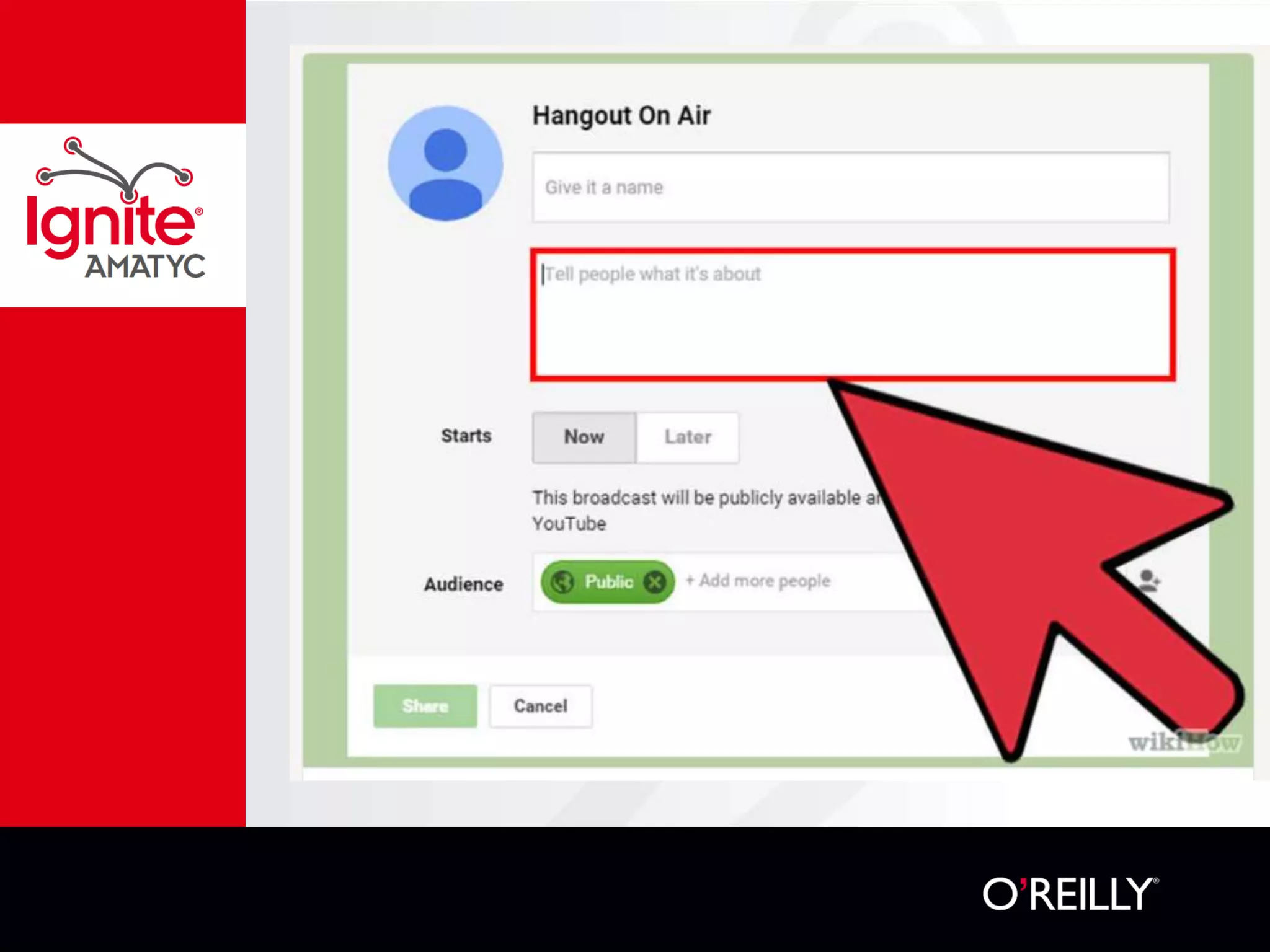
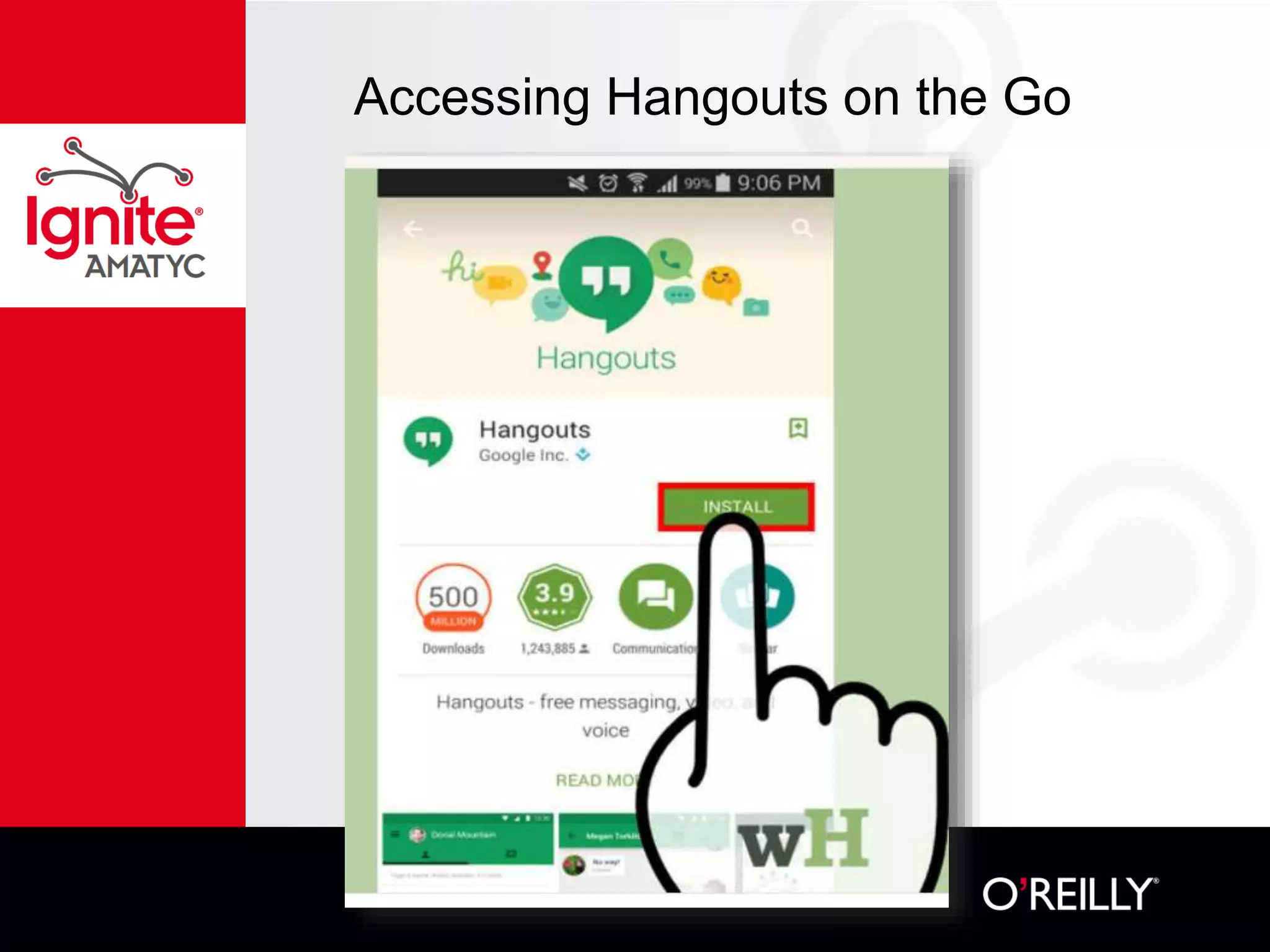
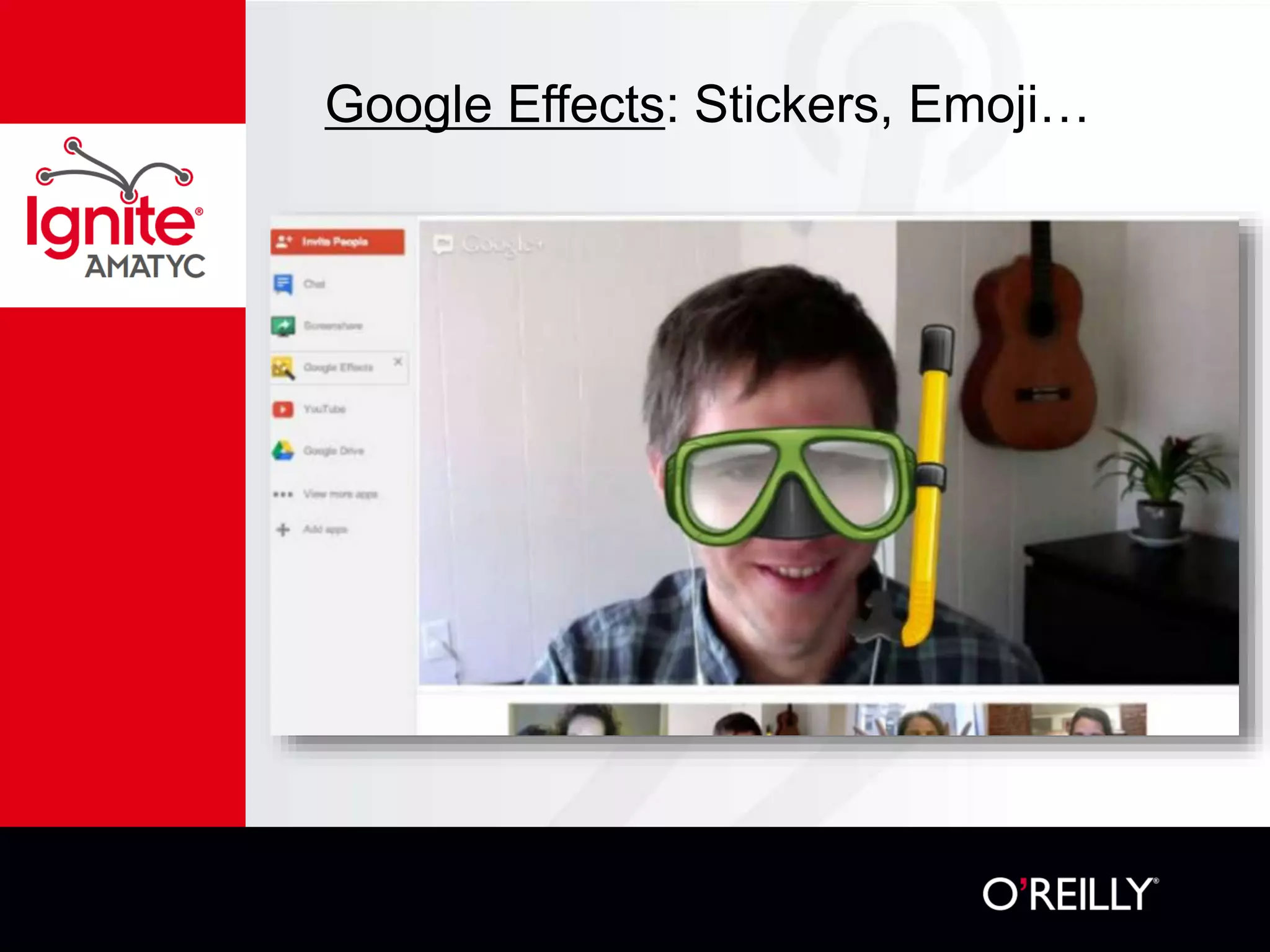
The document discusses various mathematical challenges, competitions, and educational activities involving applied math, including geometry, rates of consumption, and algebraic problems. It also highlights the importance of recognizing and correcting mathematical mistakes while engaging students through fun activities like the use of Nerf guns to demonstrate concepts. Additionally, it emphasizes utilizing real-life scenarios to enhance learning and retention of mathematical principles.