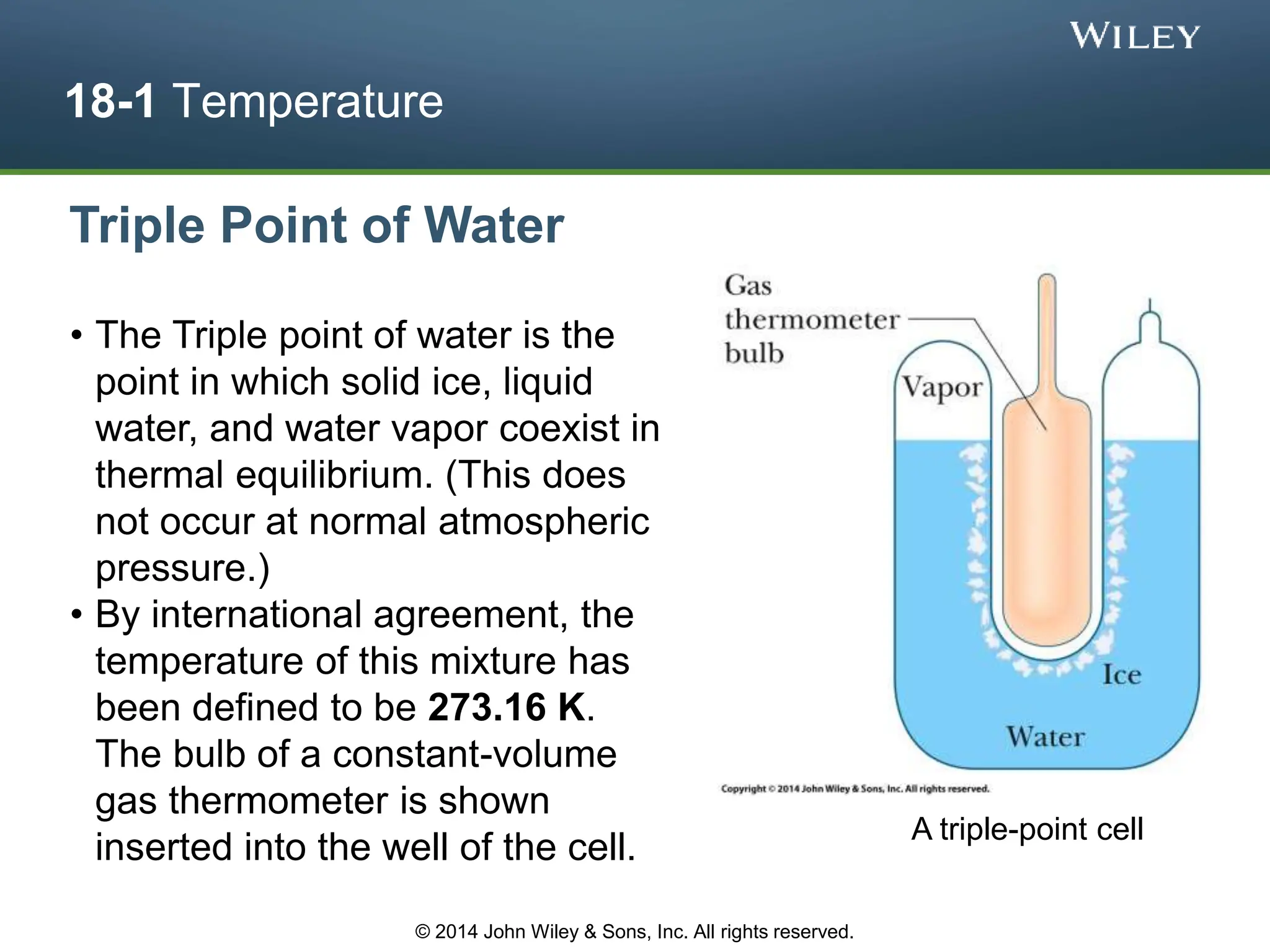
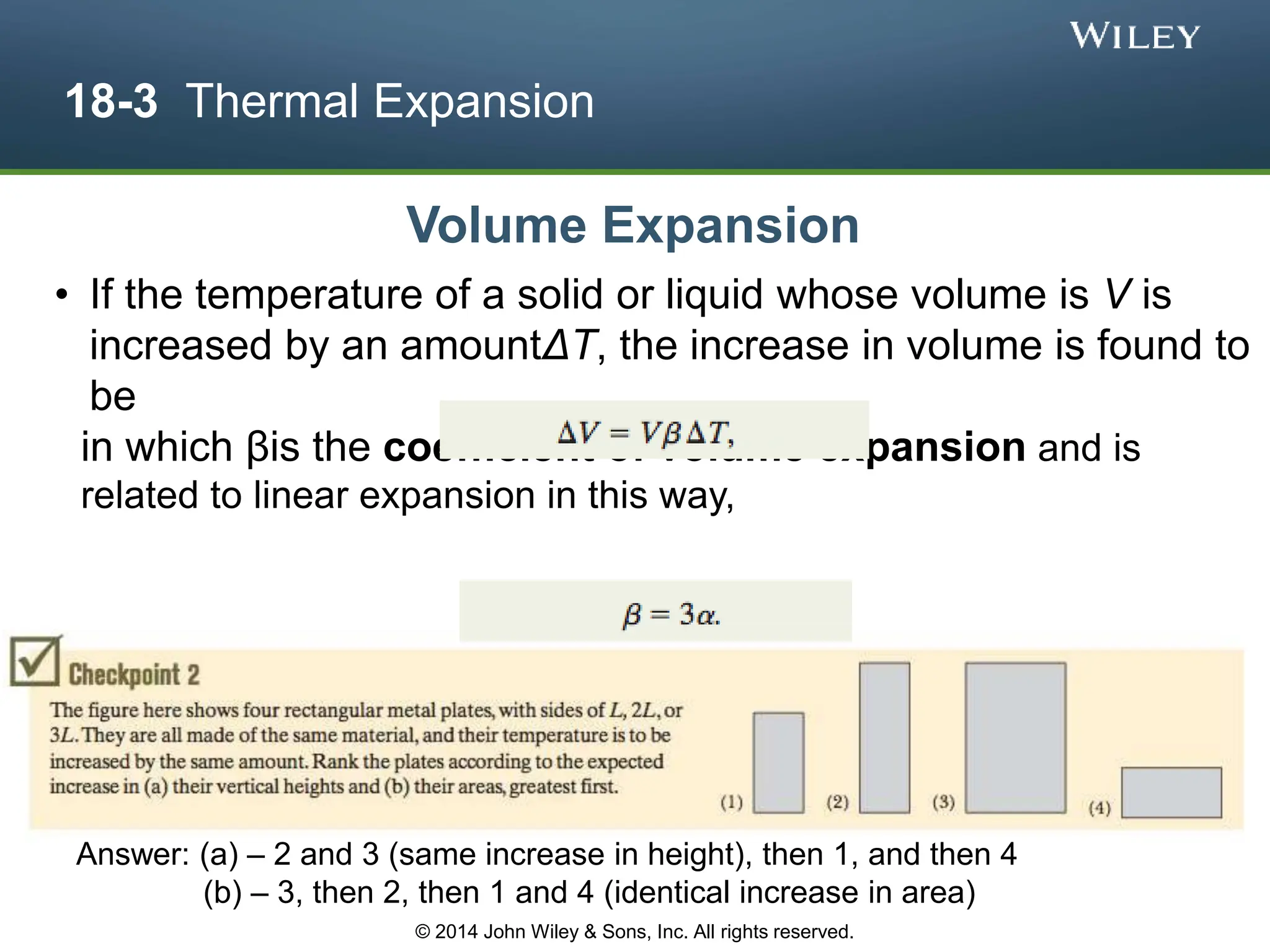
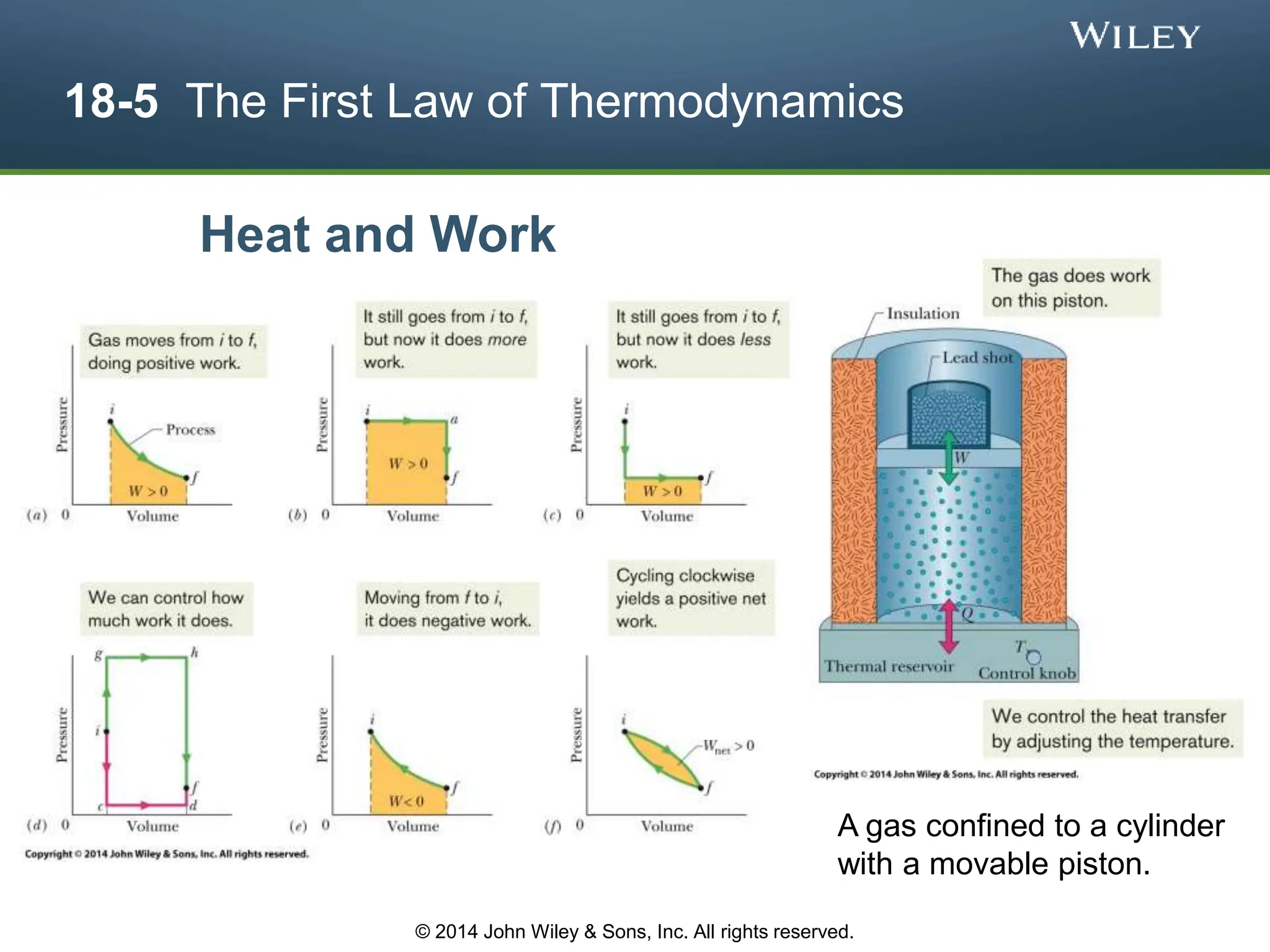
This document discusses key concepts in thermodynamics including temperature, heat transfer, and the first law of thermodynamics. It begins by defining temperature and explaining how it is measured using thermometers. The zeroth law of thermodynamics states that two bodies in thermal equilibrium with a third body are in thermal equilibrium with each other. The rest of the document discusses temperature scales, thermal expansion, mechanisms of heat transfer including conduction, convection and radiation, and how the first law relates heat, work and changes in internal energy.