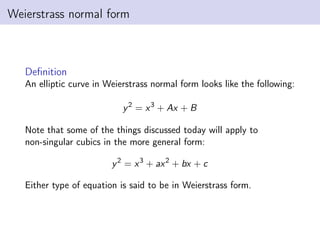
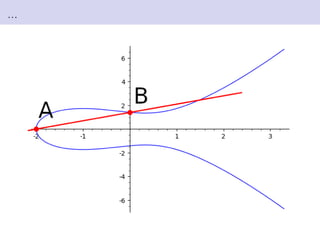
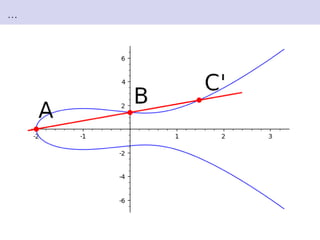
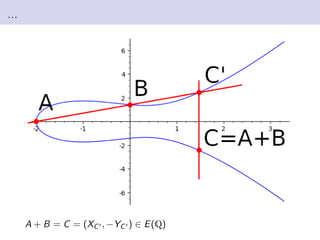
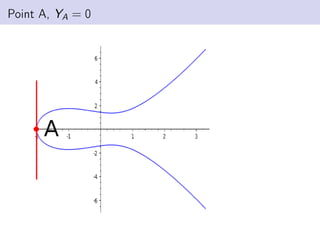
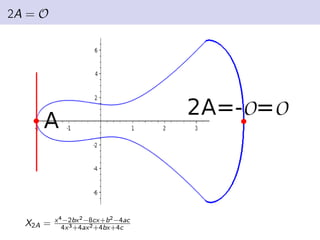
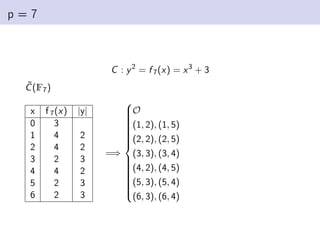
This document discusses elliptic curves in Weierstrass normal form and finding torsion points on elliptic curves. It defines Weierstrass normal form, discusses uses of elliptic curves including Andrew Wiles' proof of Fermat's Last Theorem. It also defines the group structure of elliptic curves, discusses how points are added, and defines the torsion subgroup as points of finite order. Methods for finding the torsion subgroup include reduction modulo primes and applying theorems like Nagell-Lutz. Examples are worked through on specific elliptic curves.

1. Introduction to Elliptic Curves
Finding Torsion Points
Alexander Wei
Tufts University
DRP Presentation
December 6, 2019

2. Weierstrass normal form

3. Weierstrass normal form
Definition
An elliptic curve in Weierstrass normal form looks like the following:
y2
= x3
+ Ax + B

4. Weierstrass normal form
Definition
An elliptic curve in Weierstrass normal form looks like the following:
y2
= x3
+ Ax + B
Note that some of the things discussed today will apply to
non-singular cubics in the more general form:
y2
= x3
+ ax2
+ bx + c
Either type of equation is said to be in Weierstrass form.

5. Uses of these curves
Question
What can be done with these elliptic curves?

6. Uses of these curves
Question
What can be done with these elliptic curves?
• Andrew Wiles’ proof of Fermat’s Last Theorem
@ a, b, c > 0 ∈ Z : an + bn = cn, ∀ n > 2

7. Uses of these curves
Question
What can be done with these elliptic curves?
• Andrew Wiles’ proof of Fermat’s Last Theorem
@ a, b, c > 0 ∈ Z : an + bn = cn, ∀ n > 2
• Post-quantum cryptography

8. Group structure
Definition
Let E be the non-singular elliptic curve
E : y2
= f (x) = x3
+ Ax + B.
Then E(Q) denotes the group of all points on E with rational
coordinates.
E(Q) = {(x, y) ∈ Q × Q | y2
= f (x)}.

9. Group structure
Definition
Let E be the non-singular elliptic curve
E : y2
= f (x) = x3
+ Ax + B.
Then E(Q) denotes the group of all points on E with rational
coordinates.
E(Q) = {(x, y) ∈ Q × Q | y2
= f (x)}.
Question
How are points added on an elliptic curve?

10. Group structure
Definition
Let E be the non-singular elliptic curve
E : y2
= f (x) = x3
+ Ax + B.
Then E(Q) denotes the group of all points on E with rational
coordinates.
E(Q) = {(x, y) ∈ Q × Q | y2
= f (x)}.
Question
How are points added on an elliptic curve?
Let A, B ∈ E(Q). Take the line through these two points and let
C0 be the point where it intersects E. Reflect C0 across the x-axis
to obtain the sum
A + B = C = (XC0 , −YC0 ) ∈ E(Q).

11. ...

12. ...

13. ...
A + B = C = (XC0 , −YC0 ) ∈ E(Q)

14. Point A, YA = 0

15. 2A = O

16. 2A = O
X2A = x4−2bx2−8cx+b2−4ac
4x3+4ax2+4bx+4c

17. O at infinity
Definition
There is a point O, "at infinity," in any group of points on an
elliptic curve. While it can be helpful to think of O being at an
intersection of the two ends of the curve, the ends never really
intersect. O is projective, contained in every vertical line through
the curve.
By the definition of point addition, O is the additive identity in any
group of points on elliptic curves.

18. Torsion subgroup
Theorem (Mordell, 1922)
Let C be a non-singular cubic curve given by an equation
C : y2
= x3
+ ax2
+ bx
where a and b are integers. Then the group of rational points C(Q)
is a finitely generated abelian group.

19. Torsion subgroup
Theorem (Mordell, 1922)
Let C be a non-singular cubic curve given by an equation
C : y2
= x3
+ ax2
+ bx
where a and b are integers. Then the group of rational points C(Q)
is a finitely generated abelian group.
C(Q) ∼
= Z ⊕ · · · ⊕ Z ⊕ Zp1
v1 ⊕ · · · ⊕ Zps
vs

20. Torsion subgroup
Theorem (Mordell, 1922)
Let C be a non-singular cubic curve given by an equation
C : y2
= x3
+ ax2
+ bx
where a and b are integers. Then the group of rational points C(Q)
is a finitely generated abelian group.
C(Q) ∼
= Z ⊕ · · · ⊕ Z ⊕ Zp1
v1 ⊕ · · · ⊕ Zps
vs
Definition
The torsion subgroup of the rational points on an elliptic curve C
Zp1
v1 ⊕ · · · ⊕ Zps
vs = Φ ⊆ C(Q)
Φ = {P ∈ C(Q) | ord P < ∞}

21. Mazur’s thm
Theorem (Mazur, 1978)
Let C be a non-singular rational cubic curve, and suppose that
C(Q) contains a point of finite order m. Then either
1 ≤ m ≤ 10 or m = 12

22. Mazur’s thm
Theorem (Mazur, 1978)
Let C be a non-singular rational cubic curve, and suppose that
C(Q) contains a point of finite order m. Then either
1 ≤ m ≤ 10 or m = 12
More precisely, the set of points of finite order in C(Q) forms a
subgroup that has one of the following forms:
• A cyclic group of order N with
1 ≤ N ≤ 10 or N = 12
• The product of a cyclic group of order two and a cyclic group
of order 2N with
1 ≤ N ≤ 4

23. Nagell-Lutz Theorem
Question
How might we start to learn about Φ?
Φ = {P ∈ C(Q) | ord P < ∞}

24. Nagell-Lutz Theorem
Question
How might we start to learn about Φ?
Φ = {P ∈ C(Q) | ord P < ∞}
Theorem (Nagell, 1935; Lutz, 1937)
Let C be a non-singular elliptic curve, with a point
P = (x, y) ∈ C(Q) of finite order. Then P has integer coordinates.
If y = 0, then P has order two.

25. Applying the Nagell-Lutz Theorem
C : y2
= x3
+ 3
By the Nagell-Lutz Theorem, any point P ∈ Φ will have
coordinates XP, YP ∈ Z.
The equation for C easily gives us P = (1, 2) ∈ C(Q).
Careful though!

26. Applying the Nagell-Lutz Theorem
C : y2
= x3
+ 3
By the Nagell-Lutz Theorem, any point P ∈ Φ will have
coordinates XP, YP ∈ Z.
The equation for C easily gives us P = (1, 2) ∈ C(Q).
Careful though!
Computing 2P = (−23
16 , −11
64) shows us that P /
∈ Φ.

27. Reduction Theorem
Theorem (Reduction modulo p)
Let C be a non-singular cubic curve
y2
= x3
+ ax2
+ bx + c
with a, b, c ∈ Z, and let D be the discriminant
D = −4a3
c + a2
b2
+ 18abc − 4b3
− 27c2
.

28. Reduction Theorem
Theorem (Reduction modulo p)
Let C be a non-singular cubic curve
y2
= x3
+ ax2
+ bx + c
with a, b, c ∈ Z, and let D be the discriminant
D = −4a3
c + a2
b2
+ 18abc − 4b3
− 27c2
.
Let Φ ⊆ C(Q) be the subgroup consisting of all points of finite
order. For any prime p, let P −→ P̃ be the reduction modulo p map
Φ −→ C̃(Fp), P 7−→ P̃ =
(
(x̃, ỹ) if P = (x,y),
Õ if P = O.
If p - 2D, then the reduction modulo p map is an isomorphism of Φ
onto a subgroup of C̃(Fp).

29. Applying the Reduction Theorem
Question
What is the torsion subgroup Φ of the rational points on C?
C : y2
= x3
+ 3

30. Applying the Reduction Theorem
Question
What is the torsion subgroup Φ of the rational points on C?
C : y2
= x3
+ 3
By definition of the discriminant
D = −27(3)2
= −35
.
So p > 3 ⇒ Φ ∼
= Im π = H where H is a subgroup of C̃(Fp) and π
is the reduction modulo p map
π : Φ −→ C̃(Fp).

31. p = 5
C : y2
= f 5(x) = x3
+ 3
C̃(F5)
x f 5(x) |y|
0 3
1 4 2
2 1 1
3 0 0
4 2

32. p = 5
C : y2
= f 5(x) = x3
+ 3
C̃(F5)
x f 5(x) |y|
0 3
1 4 2
2 1 1
3 0 0
4 2
=⇒











O
(1, 2), (1, 3)
(2, 1), (2, 4)
(3, 0)

33. p = 5
C : y2
= f 5(x) = x3
+ 3
C̃(F5)
x f 5(x) |y|
0 3
1 4 2
2 1 1
3 0 0
4 2
=⇒











O
(1, 2), (1, 3)
(2, 1), (2, 4)
(3, 0)
=⇒ |C̃(F5)| = 6

34. p = 7
C : y2
= f 7(x) = x3
+ 3
C̃(F7)
x f 7(x) |y|
0 3
1 4 2
2 4 2
3 2 3
4 4 2
5 2 3
6 2 3

35. p = 7
C : y2
= f 7(x) = x3
+ 3
C̃(F7)
x f 7(x) |y|
0 3
1 4 2
2 4 2
3 2 3
4 4 2
5 2 3
6 2 3
=⇒

























O
(1, 2), (1, 5)
(2, 2), (2, 5)
(3, 3), (3, 4)
(4, 2), (4, 5)
(5, 3), (5, 4)
(6, 3), (6, 4)

36. p = 7
C : y2
= f 7(x) = x3
+ 3
C̃(F7)
x f 7(x) |y|
0 3
1 4 2
2 4 2
3 2 3
4 4 2
5 2 3
6 2 3
=⇒

























O
(1, 2), (1, 5)
(2, 2), (2, 5)
(3, 3), (3, 4)
(4, 2), (4, 5)
(5, 3), (5, 4)
(6, 3), (6, 4)
=⇒ |C̃(F7)| = 13

37. Φ found?
Let Φ be the torsion subgroup of the rational points on C, |Φ| = n.
Computing the points C̃(F5) and C̃(F7) tells us that |C̃(F5)| = 6
and |C̃(F7)| = 13.

38. Φ found?
Let Φ be the torsion subgroup of the rational points on C, |Φ| = n.
Computing the points C̃(F5) and C̃(F7) tells us that |C̃(F5)| = 6
and |C̃(F7)| = 13.
The Reduction (mod p) Theorem
⇒ Φ ⊆ C̃(F5) and Φ ⊆ C̃(F7).
∴ Lagrange’s Theorem ⇒ n | 6 and n | 13.

39. Φ found?
Let Φ be the torsion subgroup of the rational points on C, |Φ| = n.
Computing the points C̃(F5) and C̃(F7) tells us that |C̃(F5)| = 6
and |C̃(F7)| = 13.
The Reduction (mod p) Theorem
⇒ Φ ⊆ C̃(F5) and Φ ⊆ C̃(F7).
∴ Lagrange’s Theorem ⇒ n | 6 and n | 13.
∴ n = 1, so Φ is the trivial group
Φ = {O}.

40. Applying the Reduction Theorem
Question
What is the torsion subgroup Φ of the rational points on C?
C : y2
= x3
+ x

41. Applying the Reduction Theorem
Question
What is the torsion subgroup Φ of the rational points on C?
C : y2
= x3
+ x
By definition of the discriminant
D = −4 = −22
.
So p > 2 ⇒ Φ ∼
= Im π = H where H is a subgroup of C̃(Fp) and π
is the reduction modulo p map
π : Φ −→ C̃(Fp).

42. p = 3
C : y2
= f 3(x) = x3
+ x
C̃(F3)
x f 3(x) |y|
0 0 0
1 2
2 1 1

43. p = 3
C : y2
= f 3(x) = x3
+ x
C̃(F3)
x f 3(x) |y|
0 0 0
1 2
2 1 1
=⇒





O
(0, 0)
(2, 1), (2, 2)

44. p = 3
C : y2
= f 3(x) = x3
+ x
C̃(F3)
x f 3(x) |y|
0 0 0
1 2
2 1 1
=⇒





O
(0, 0)
(2, 1), (2, 2)
=⇒ |C̃(F3)| = 4

45. p = 5
C : y2
= f 5(x) = x3
+ x
C̃(F5)
x f 5(x) |y|
0 0 0
1 2
2 0 0
3 0 0
4 3

46. p = 5
C : y2
= f 5(x) = x3
+ x
C̃(F5)
x f 5(x) |y|
0 0 0
1 2
2 0 0
3 0 0
4 3
=⇒











O
(0, 0)
(2, 0)
(3, 0)

47. p = 5
C : y2
= f 5(x) = x3
+ x
C̃(F5)
x f 5(x) |y|
0 0 0
1 2
2 0 0
3 0 0
4 3
=⇒











O
(0, 0)
(2, 0)
(3, 0)
=⇒ |C̃(F5)| = 4

48. Φ found.
Let Φ be the torsion subgroup of the rational points on C, |Φ| = n.
Computing the points C̃(F3) and C̃(F5) tells us that |C̃(F3)| = 4
and |C̃(F5)| = 4.

49. Φ found.
Let Φ be the torsion subgroup of the rational points on C, |Φ| = n.
Computing the points C̃(F3) and C̃(F5) tells us that |C̃(F3)| = 4
and |C̃(F5)| = 4.
C̃(F3) has one point with y-coordinate zero and C̃(F5) has three
points with YP = 0.
Nagell-Lutz ⇒ C̃(F3) ∼
= Z4 and C̃(F5) ∼
= Z2 ⊕ Z2

50. Φ found.
Let Φ be the torsion subgroup of the rational points on C, |Φ| = n.
Computing the points C̃(F3) and C̃(F5) tells us that |C̃(F3)| = 4
and |C̃(F5)| = 4.
C̃(F3) has one point with y-coordinate zero and C̃(F5) has three
points with YP = 0.
Nagell-Lutz ⇒ C̃(F3) ∼
= Z4 and C̃(F5) ∼
= Z2 ⊕ Z2
The Reduction (mod p) Theorem
⇒ Φ ⊆ Z4
∼
= C̃(F5) and Φ ⊆ Z2 ⊕ Z2
∼
= C̃(F7).
∴ Φ is either trivial or cyclic of order two.

51. Φ found.
Let Φ be the torsion subgroup of the rational points on C, |Φ| = n.
Computing the points C̃(F3) and C̃(F5) tells us that |C̃(F3)| = 4
and |C̃(F5)| = 4.
C̃(F3) has one point with y-coordinate zero and C̃(F5) has three
points with YP = 0.
Nagell-Lutz ⇒ C̃(F3) ∼
= Z4 and C̃(F5) ∼
= Z2 ⊕ Z2
The Reduction (mod p) Theorem
⇒ Φ ⊆ Z4
∼
= C̃(F5) and Φ ⊆ Z2 ⊕ Z2
∼
= C̃(F7).
∴ Φ is either trivial or cyclic of order two.
Note P = (0, 0) ∈ C(Q), 2P = O.

52. Φ found.
Let Φ be the torsion subgroup of the rational points on C, |Φ| = n.
Computing the points C̃(F3) and C̃(F5) tells us that |C̃(F3)| = 4
and |C̃(F5)| = 4.
C̃(F3) has one point with y-coordinate zero and C̃(F5) has three
points with YP = 0.
Nagell-Lutz ⇒ C̃(F3) ∼
= Z4 and C̃(F5) ∼
= Z2 ⊕ Z2
The Reduction (mod p) Theorem
⇒ Φ ⊆ Z4
∼
= C̃(F5) and Φ ⊆ Z2 ⊕ Z2
∼
= C̃(F7).
∴ Φ is either trivial or cyclic of order two.
Note P = (0, 0) ∈ C(Q), 2P = O.
∴ Φ = {(0, 0), O} ∼
= Z2.

53. So we found Φ.
Thank you!