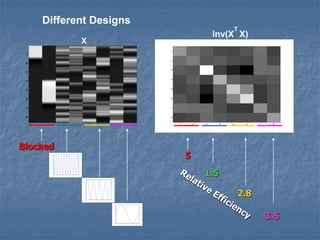
Margarita Sarri and Hugo Spiers discuss experimental design and estimation efficiency in event-related functional MRI. They cover different types of designs including blocked and event-related, as well as how to order events. Estimation efficiency depends on the design matrix and can be calculated to determine which designs are most powerful for detecting effects of interest. Both the order of trials and spacing of events, such as the stimulus onset asynchrony, impact efficiency. While blocked designs tend to be most efficient, some randomized event-related designs can also achieve high efficiency depending on the specific contrasts and hypotheses being tested.

1. Study Design and Efficiency
Margarita Sarri
Hugo Spiers

2. We will talk about:
 What kinds of designs are out there? -
Blocked vs event-related designs
 How can I order my events?
 What is estimation efficiency?
 Which designs are more efficient?
 Spacing of events
 Sampling issues
 Filtering issues

3. Event related vs Blocked designs
 Blocked / Epoch/ Box design
 Types of trials are ‘blocked’ together e.g. AAAAA BBBBB
AAAAA.
 Event related design
 Types of trials are interleaved and each trial is modelled separately as
an ‘event’ e.g. AABABBAB

4.  In general 2 blocks more efficient than 4.
 Ideal modulation frequency being approximately 16sec
but you may not be able to test certain things with such a design…
So you may want to go for an event related design…
Blocked design
 typically used in experiments where the detection of activation is the primary
goal.
 e.g localise a specific brain region showing a differential response to one type
of stimulus (e.g. faces vs houses)

5. Why should I use efMRI ?
 Flexibility and randomization
 eliminate predictability of block designs
 avoid practice effects/strategy use
 Post hoc sorting
 e.g. classification of correct vs. incorrect, subjective perception:
aware vs. unaware, remembered vs. forgotten items, parametric
scores: e.g. fast vs. slow RTs
 Measuring novelty: Rare or unpredictable events
 e.g. oddball designs.
 Allows to look at events on a shorter time scale.
P
L
H
A
K

6. But you can also combine block and efMRI…
A block can be treated as a continuous train of event-trials
 E.g Otten, Henson & Rugg, Nature Neuroscience 2002
‘Subsequent memory’ experiment separating transient (events) and
sustained (blocks) neural activity.
At the beginning of each trial a cue instructed subjects to make an
phonological or semantic judgement.
83sec rest 83sec

7. Hmmm I think I like efMRI.
But how do I order my
trials?

8. efMRI: Sequencing of events
Deterministic
designs:
the occurrence of events
is pre-determined e.g. a
blocked design or
alternating design (all the
probabilities are zero or one )
Stochastic
designs:
the occurrence of
an event depends
on a a specified
probability e.g.
random or
permuted design
Stochastic designs
can be stationary or
dynamic
Blocked
Alternating
1 2 3 4 5 6 7 8
10
20
30
40
50
60
70
80
Random
Permuted

10. How do I do I create a permuted order of
events?
ensure mini-runs of same stimuli…
i.e. modulate the probability of different event-types over experimental time

11. Permutation methods continued…

13. So what is
Efficiency?

14. Efficiency is…
 Efficiency is a numerical value
which reflects the ability of your design to detect the effect of
interest
 General Linear Model:
Y = X . β + e
Data Design Matrix Parameters error
 Efficiency is the ability to estimate β, given the design matrix X
 Efficiency can be calculated because the variance of β is proportional
to the variance of X

15. What is variance?
Standard
Deviation
 Variance = Standard Deviation 2
High Variance
Low Variance
Standard
Deviation

16. Testing a Hypothesis
T- Test for the difference between 2 conditions
Lower ability to detect a difference
Higher ability to detect a difference
Standard
Deviation
Standard
Deviation
• By reducing the variance in the design we can maximize our T values

17. How do we calculate it?
 Efficiency  Inverse( Var(β) )
 Inverse( Var(β) )  Var(X)
 Var(X)  Inverse( XT
X )

18. A B C D
1 0 0 0
1 0 0 0
1 0 0 0
1 0 0 0
1 0 0 0
0 1 0 0
0 1 0 0
0 1 0 0
0 1 0 0
0 1 0 0
0 0 0 0
0 0 0 0
0 0 1 0
0 0 1 1
0 0 1 1
0 0 1 1
0 0 1 1
0 0 0 1
0 0 0 0
0 0 0 0
X X
T
A 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
B 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
C 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0
D 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0
. =
A B C D
A 5 0 0 0
B 0 5 0 0
C 0 0 5 4
D 0 0 4 5
X
T
X
Non-
overlapping
conditions
Overlapping
conditions

19. A B C D
A 5 0 0 0
B 0 5 0 0
C 0 0 5 4
D 0 0 4 5
X
T
X inverse (X
T
X)
A B C D
A 0.2 0 0 0
B 0 0.2 0 0
C 0 0 0.6 -0.4
D 0 0 -0.4 0.6

20. The efficiency is related to the specific
contrast you are interested in
Efficiency = inverse(σ2 cT Inverse(XTX) c)
Where c = contrast
σ2 = noise variance
But if we assume that noise variance σ2 is constant then:
Efficiency = inverse (cT Inverse (XTX) c)

21. When c is Simple Effect,
e.g. main effect of A c = [1 0 0 0]
inverse(X
T
X)
A B C D
A 0.2 0 0 0
B 0 0.2 0 0
C 0 0 0.6 -0.4
D 0 0 -0.4 0.6
Efficiency = Inverse( cT Inverse(XTX) c)
A, B: Efficiency = 1 / 0.2 = 5
C, D: Efficiency = 1 / 0.6 = 1.7
1
0
0
0
1 0 0 0
CT
C

22. When c is contrast difference,
e.g. For A – B c = [1 -1 0 0]
inverse(X
T
X)
A B C D
A 0.2 0 0 0
B 0 0.2 0 0
C 0 0 0.6 -0.4
D 0 0 -0.4 0.6
Efficiency = Inverse( cT Inverse(XTX) c)
A-B: Efficiency = 1 / 0.4 = 2.5
C-D: Efficiency = 1 / 2 = 0.5
1
-1
0
0
1 -1 0 0
CT
C

23. 0.5 1 1.5 2 2.5 3 3.5 4 4.5
100
200
300
400
500
600
700
800
900
Variable No. of Trials
X inv(X
T
X)
4.2
Random:
Events =
25
2.1
Relative Efficiency
Random:
Events =
50
0.5 1 1.5 2 2.5 3 3.5 4 4.5
0.5
1
1.5
2
2.5
3
3.5
4
4.5

24. How does trial order effect
Efficiency?

25. Example

26. A B C D E F
1 0 0 0 0 0
1 0 1 0 0 1
1 0 0 0 0 1
1 0 0 1 0 0
1 0 0 0 0 0
0 1 1 0 0 0
0 1 0 0 0 0
0 1 0 1 1 0
0 1 0 0 1 0
0 1 1 0 0 1
0 0 0 0 0 0
0 0 0 1 0 1
0 0 0 0 1 0
0 0 1 0 1 0
0 0 0 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 1 0 0 0
0 0 0 0 0 1
0 0 0 1 0 0
Different Designs – Boxcar Events
inv(X
T
X)
A B C D E F
A 0.2488 0.0377 -0.0297 -0.0396 -0.0012 -0.0873
B 0.0377 0.2862 -0.0941 -0.0421 -0.0873 -0.0263
C -0.0297 -0.0941 0.2871 0.0495 -0.0297 -0.0941
D -0.0396 -0.0421 0.0495 0.2327 -0.0396 -0.0421
E -0.0012 -0.0873 -0.0297 -0.0396 0.2488 0.0377
F -0.0873 -0.0263 -0.0941 -0.0421 0.0377 0.2862
1 2 3 4 5 6
1
2
3
4
5
6
X
Blocked
Fixed
Interleaved
Random

27. 1.5
Different Designs
Blocked
Fixed
Interleaved
Random-
Uniform
1 2 3 4 5 6 7 8
10
20
30
40
50
60
70
80
Random-
Sinusoidal
1 2 3 4 5 6 7 8
1
2
3
4
5
6
7
8
inv(X
T
X)
X
5
2.8
3.5

28. 1 2 3 4 5 6 7 8
1
2
3
4
5
6
7
8
Different Designs
1.5
Blocked
X
5
2.8
3.5
inv(X
T
X)
10
20
30
40
50
60
70
80
0 5 10 15 20 25 30 35 40
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
0 5 10 15 20 25 30 35 40
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
0 5 10 15 20 25 30 35 40
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1

29. Sequencing of events
Stochastic designs: at each
point at which an event could
occur there is a specified
probability of that event
occurring. The timing of when
the events occur is specified.
Non-occurrence = null event.
Deterministic designs: the
occurrence of events is pre-
determined.
The variable deterministic
design i.e. a blocked design,
is the most efficient.

30. Joel’s example of different stimulus presentations
Blocked
design
Fully
randomised
Dynamic
stochastic
A B C
Tasks
0
10
20
30
40
50
60
70
80
90
100
Block Dynamic
stochastic
Randomised
Efficiency calculation

32. different designs
{
minimum SOA (inter-stimulus interval)
probability of occurrence

33. How fast can I present my
trials?

34. The absolute minimum…
 Early event-related fMRI studies used a long Stimulus
Onset Asynchrony (SOA) to allow BOLD response to
return to baseline (20-30s).
 However, if the BOLD response is explicitly modelled,
overlap between successive responses at short SOAs can
be accommodated… (assuming that successive responses
add up in a linear fashion)
 The lower limit on SOAs is dictated by nonlinear interactions
among events that can be though of as saturation phenomena or
‘‘refractoriness’’ at a neuronal or hemodynamic level.
 But, very short SOAs (< 1s) are not advisable as the
predicted additive effects upon the HRF of two closely
occurring stimuli break down.
Brief
Stimulus
Undershoot
Initial
Undershoot
Peak
So you can have events occurring even every 1-2 sec!
But think of psychological validity!
max.
oxygenation: 4-
6s post-stimulus

35. And how should my events
be spaced? optimal SOA

36. Choosing the best SOA
 Optimal SOA depends on:
 Probability of occurrence (design)
 Whether one is looking for evoked responses per
se or differences in evoked responses.
Generally SOAs that are small and randomly distributed are the most efficient.
Rapid presentation rates allow for the
maintenance of a particular cognitive or
attentional set, decrease the latitude that the
subject has for engaging alternative
strategies, or incidental processing.
Random SOAs ensure
that preparatory or
anticipatory
factors do not confound
event-related responses
and ensure a uniform
context in which events
are presented.

37. Probability
SOA
ONE TRIAL TYPE TWO TRIAL TYPES
Main effect
Differential responses
the most efficient SOA for differential responses is very small.
longer SOAs of around 16 s are necessary to estimate the responses themselves.
Stationary Stochastic designs

38. What should I do if I am interested in
the main effects (‘evoked responses’)?
 You can use long SOA’s (around 16 secs!).
But behaviourally this may be inefficient
 So you can introduce ‘null’ events and
keep your SOA short.
 These null events now provide a baseline
against which the response to either trial
type 1 or 2 can be estimated even using a
very small SOA. (p=0.5 0.3)
to identify areas that are activated by both event types

39. Here is what happens when you add null events…
Random
Note that although null events increase efficiency for main effects (at
short SOA’s), they slightly decrease efficiency for differential effects

40. What should I do if I am interested in the differential effects?
For very short SOA’s use a randomised design
But for medium SOA’s a permuted (4-6sec) or an alternating (8sec) design is better

41. To sum up: Remember that…
 Blocked designs generally more efficient
 Some random event-related designs are much
better than others.
 Different design is appropriate depending on
what you want to optimize.
 Critical properties to optimize
 Ordering of trials
 spacing between stimuli

43. Timing of the SOAs in relation to the TR
 If the TR (Repetition Time of slice collection) is divisible by the SOA then data
collected for each event will be from the same slices, at the same points along the
HRF.
 Therefore, either choose a TR and SOA that are not divisible or introduce a ‘jitter’
such that the SOA is randomly shifted.
Scans TR = 4s
Stimulus (synchronous) SOA=8s
Stimulus (asynchronous) SOA=6s
Stimulus (random jitter)

44. Temporal Filtering: The High Pass Filter
 A temporal filter is used in fMRI to get rid
of noise, thus increasing the efficiency of
the data.
 Non-neuronal noise tends to be of low-
frequency, including ‘scanner drift’ and
physiological phenomenon.
 Applying a high pass filter means that
parameters that occur at a slow rate are
removed from the analysis.
 The default high pass filter in SPM is 128s,
thus if you have experimental events
occurring less frequently than once every
128s then the associated signal will be
removed by the filter!!

45. Sources

46. Summary
 Blocked designs are generally the most efficient, but blocked
designs have restrictions.
 For event-related designs, dynamic stochastic presentation of stimuli
is most efficient.
 However, the most optimal design for your data depends on the
SOA that you use. The general rule is the smaller your SOA the
better, but sometimes a small SOA may not be possible.
 Also, the most optimal design for one contrast may not be optimal
for another e.g. the inclusion of null events improves the efficiency
of main effects at short SOAs, at the cost of efficiency for
differential effects.
 Finally, there is no point scanning two tasks to look for differences
between them if they are too different or too similar.