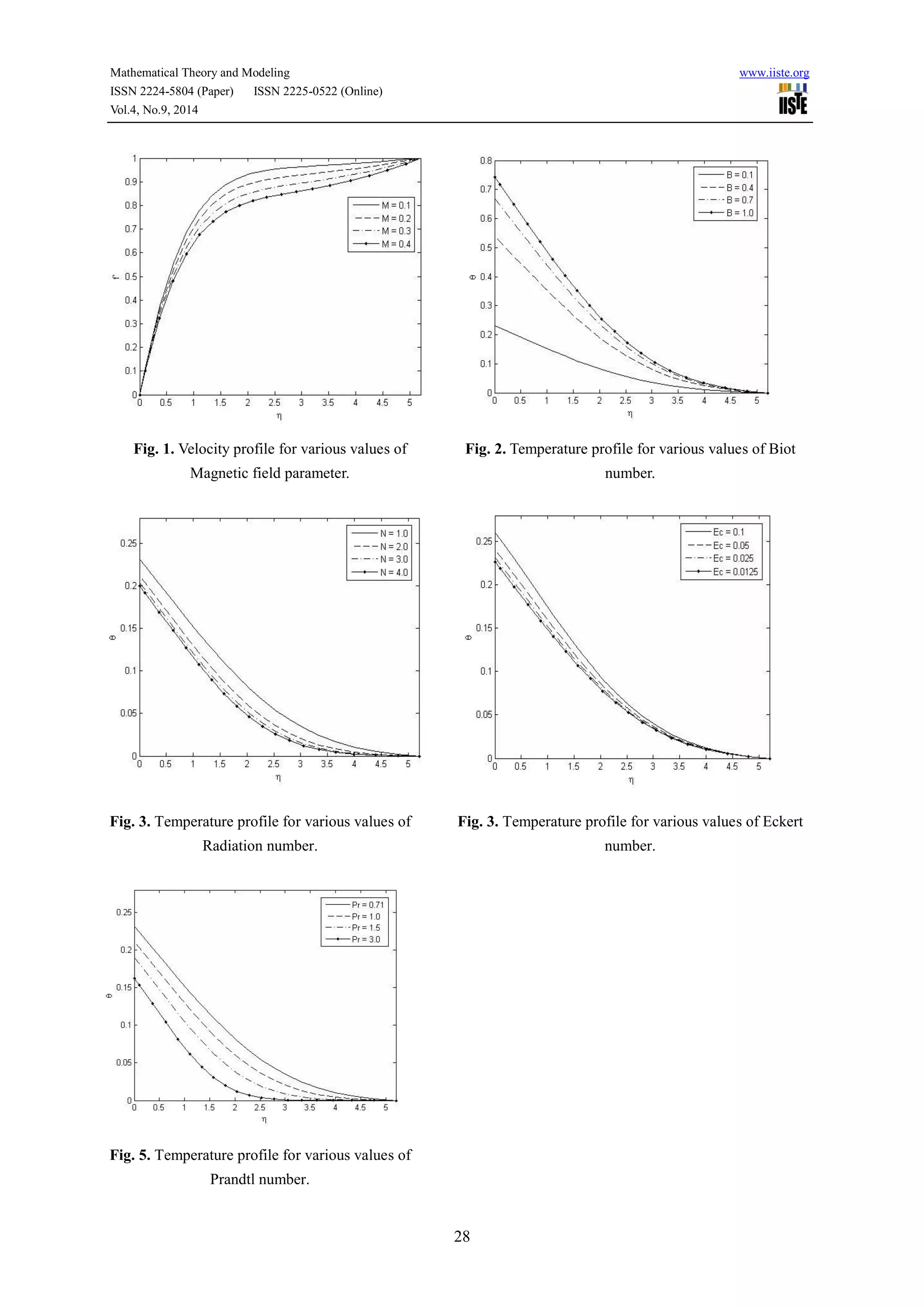
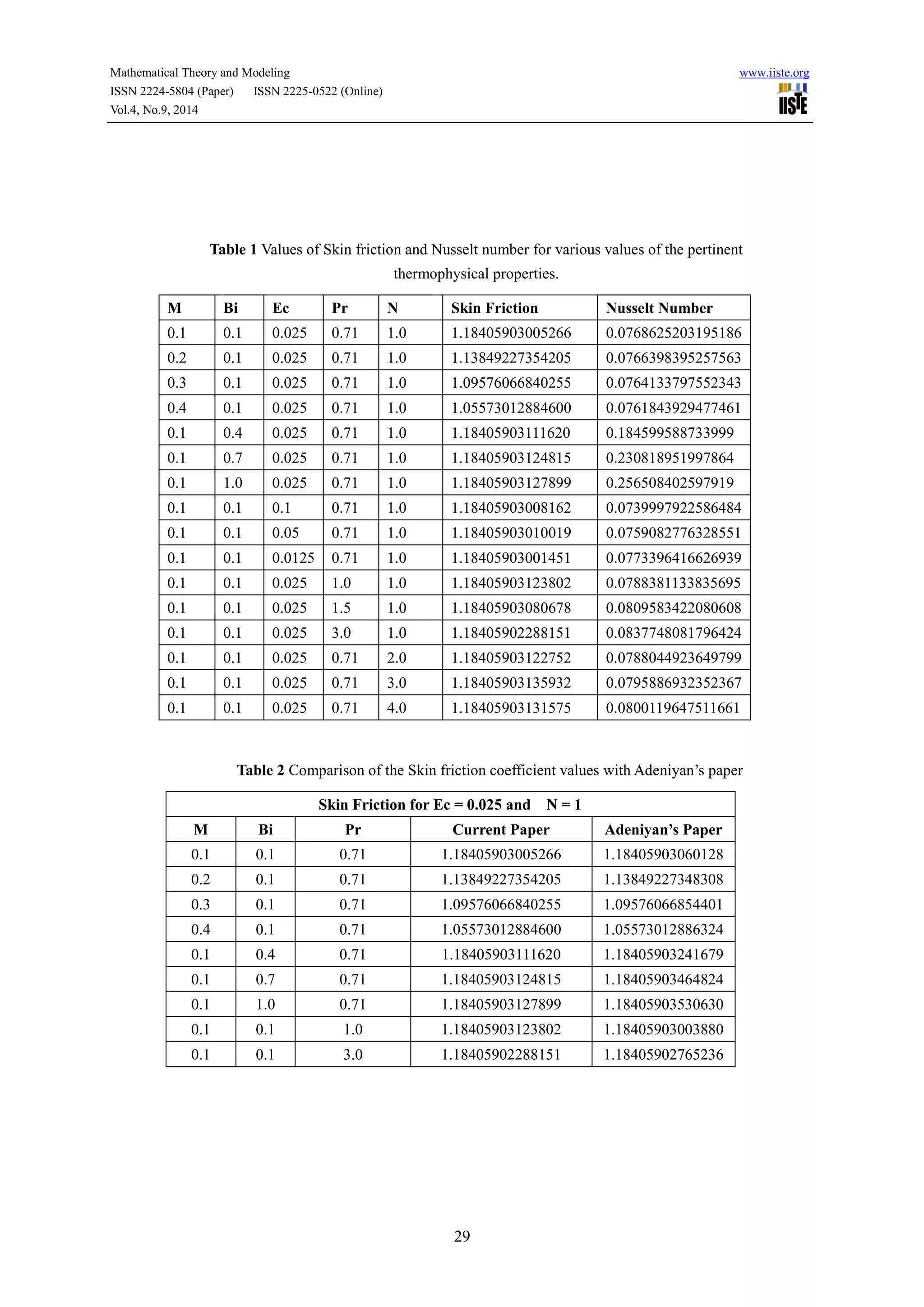
This document presents research on force convective stagnation point flow over a stretching sheet with convective boundary conditions in the presence of thermal radiation and a magnetic field. Governing equations for the flow are derived and non-dimensionalized. The equations are then solved numerically using a shooting method. Results show that increasing the magnetic field parameter decreases velocity, while increasing the Biot number increases temperature. Temperature is also found to decrease with increasing Eckert number, Prandtl number, and radiation parameter. Skin friction coefficient and local Nusselt number are presented for various parameter values.