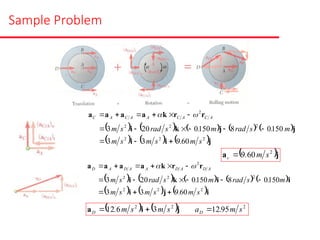
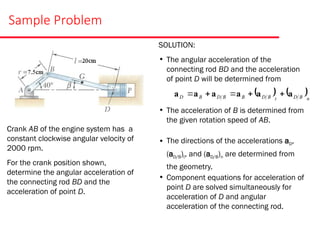
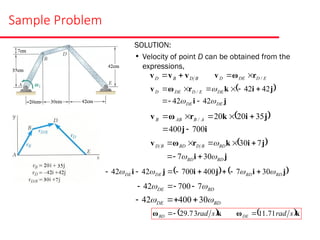
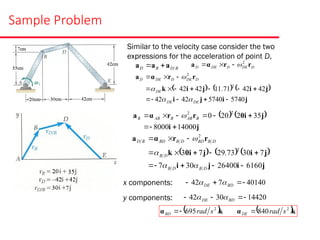
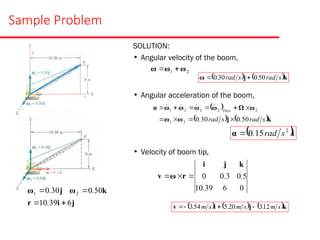
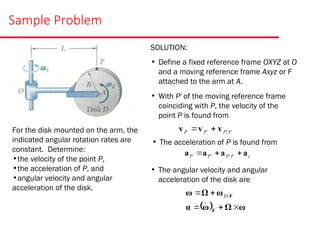
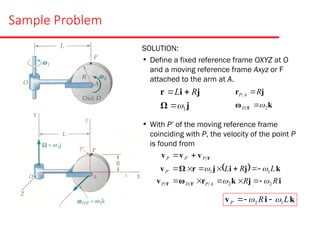
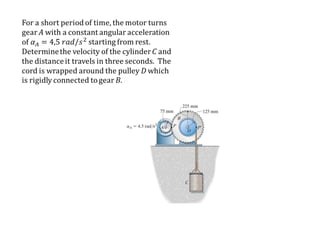
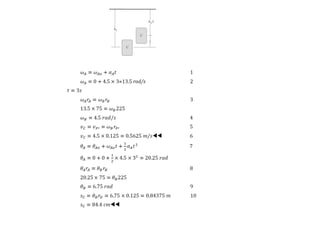
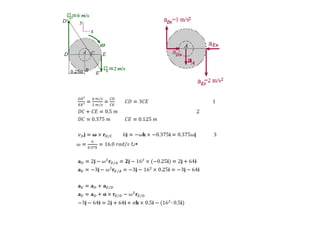
The document presents various sample problems related to dynamics, particularly focusing on the acceleration, velocity, and angular motion of different mechanical systems involving pulleys, gears, and connecting rods. Each problem includes detailed calculations and solutions for parameters such as revolutions, tangential and normal acceleration, and angular velocity. It emphasizes the application of relationships in uniformly accelerated rotation and the principles of motion in mechanical systems.

1. Asst. Prof. Murat Saribay
Bilgi University
ME 232 Dynamics (Chapter V - Examples)

2. Sample Problem
Cable C has a constant acceleration of 225
mm/s2
and an initial velocity of 300 mm/s,
both directed to the right.
Determine (a) the number of revolutions
executed by the pulley in 2 s, (b) the
velocity and change in position of the load B
after 2 s, and (c) the acceleration of the
point D on the rim of the inner pulley at t=0.
SOLUTION:
• Due to the action of the cable, the
tangential velocity and acceleration of
D are equal to the velocity and
acceleration of C. Calculate the initial
angular velocity and acceleration.
• Apply the relations for uniformly
accelerated rotation to determine the
velocity and angular position of the
pulley after 2 s.
• Evaluate the initial tangential and
normal acceleration components of D.

3. Sample Problem
SOLUTION:
• The tangential velocity and acceleration of D are equal to
the velocity and acceleration of C.
   
 
 
s
rad
r
v
r
v
s
mm.
D
D
C
D
4
75
300
300
0
0
0
0
0
0









v
v  
 
  2
2
3
75
225
225
s
rad
r
a
r
a
s
mm.
t
D
t
D
C
t
D









a
a
• Apply the relations for uniformly accelerated rotation to determine velocity
and angular position of pulley after 2s.
   s
rad
s
s
rad
s
rad
αt
ω
ω 10
2
3
4 2
0 




      rad
s
s
rad
s
s
rad
t
t 14
2
3
2
4
2
2
2
1
2
2
1
0 



 


  revs
of
number
rad
2
rev
1
rad
14 








N rev
23
.
2

N
  
  
rad
mm
rθ
Δy
s
rad
mm
rω
v
B
B
14
125
10
125




mm
Δy
s
mm
B
B
1750
1250



v

4. Sample Problem
• Evaluate the initial tangential and normal
acceleration components of D.
  

 s
mm
C
t
D 225
a
a
     2
2
2
0 1200
4
75 s
mm
s
rad
mm
ω
r
a D
n
D 


    


 2
2
1200
225 s
mm
s
mm n
D
t
D a
a
   
2
2
2
2
1200
225 


 n
D
t
D
D a
a
a
2
9
1220 s
mm
.
aD 
 
 
225
1200


t
D
n
D
a
a
tan

 4
.
79


5. Sample Problem
The pinion A of the hoist motor drives gear
B, which is attached to the hoisting drum.
The load L is lifted from its rest position and
acquires an upward velocity of 2 m/s in a
vertical rise of 0.8 m with constant
acceleration. As the load passes this
position, compute (a) the acceleration of
point C on the cable in contact with the
drum and (b) the angular velocity and
angular acceleration of the pinion A.
(a) The load is raised by a constant
acceleration. Initially at rest and reaches a
velocity of 2 m/s after travelling a distance
of 0.8m. Thus the acceleration is:
The point C has a tangential acceleration
that is equal to the acceleration of the load
Similarly, the point C has a velocity equal
to the velocity of the load,
s
a
v
v L
Lo
L 2
2
2


 
8
0
2
0
22
.
aL


L
a
s
/
m
. 
2
5
2
  2
5
2 s
/
m
.
a t
C 
s
/
m
v
v L
C 2



6. Sample Problem
Thus, the normal component of the acceleration of point
C is,
The total acceleration is then,
Angular motion of A is determined from the angular
motion of gear B. The point of contact between these two
gears has the common velocity v1 and acceleration a1.
Angular velocity of B is determined from the velocity of
point C;
L
a
s
/
m
. 
2
5
2
  2
5
2 s
/
m
.
a t
C 
s
/
m
v
v L
C 2


  2
2
2
10
4
0
2
s
/
m
.
v
a C
n
C 



    2
2
2
2
2
31
10
10
5
2 s
/
m
.
.
a
a
a n
C
t
C
C 




B
C
C r
v 


B
. 

4
0
2  CCW
s
/
rad
B 5




7. Sample Problem
The tangential component of the acceleration of point C is,
Thus, the velocity and tangential acceleration of point 1 on
gear B are,
The velocity and tangential acceleration of point 1 on gear
A are,
L
a
s
/
m
. 
2
5
2
  2
5
2 s
/
m
.
a t
C 
s
/
m
v
v L
C 2


CCW
s
/
rad
B 5



  C
B
t
C r
a 

 B
.
. 

4
0
5
2 
CCW
s
/
rad
.
B
2
25
6



  1
1 r
a B
t



B
r
v 

1
1  s
/
m
.
.
v 5
1
5
3
0
1 


  2
1 875
1
25
6
3
0 s
/
m
.
.
.
a t



A
A
r
v 

1
1  CW
s
/
rad
.
. A
A 15
1
0
5
1 

 
 

  A
A
t
A r
a 1
1 


CW
s
/
rad
.
.
. A
A
2
75
18
1
0
875
1 

 
 



◄
◄

8. Sample Problem
The center of the double gear has a
velocity and acceleration to the right
of 1.2 m/s and 3 m/s2
, respectively.
The lower rack is stationary.
Determine (a) the angular acceleration
of the gear, and (b) the acceleration of
points B, C, and D.
SOLUTION:
• The expression of the gear position as a
function of q is differentiated twice to
define the relationship between the
translational and angular accelerations.
• The acceleration of each point on the
gear is obtained by adding the
acceleration of the gear center and the
relative accelerations with respect to
the center. The latter includes normal
and tangential acceleration
components.

9. Sample Problem
SOLUTION:
• The expression of the gear position as a function of
q is differentiated twice to define the relationship
between the translational and angular
accelerations.



1
1
1
r
r
v
r
x
A
A







s
rad
8
m
0.150
s
m
2
.
1
1






r
vA


 1
1 r
r
aA 


 

m
150
.
0
s
m
3 2
1




r
aA

 k
k
α 2
20 s
rad




10. Sample Problem
• The acceleration of each
point is obtained by
adding the acceleration of
the gear center and the
relative accelerations with
respect to the center.
The latter includes normal
and tangential acceleration
components.
   
         
     j
i
i
j
j
k
i
r
r
k
a
a
a
a
a
a
a
2
2
2
2
2
2
2
40
6
2
3
100
0
8
100
0
20
3
s
m
.
s
m
s
m
m
.
s
rad
m
.
s
rad
s
m
ω
α A
B
A
B
A
n
A
B
t
A
B
A
A
B
A
B

















    2
2
2
12
8
40
6
5 s
m
.
a
s
m
.
s
m B
B 

 j
i
a

11. Sample Problem
         
     j
i
i
j
j
k
i
r
r
k
a
a
a
a
2
2
2
2
2
2
2
60
9
3
3
150
0
8
150
0
20
3
s
m
.
s
m
s
m
m
.
s
rad
m
.
s
rad
s
m
A
C
A
C
A
A
C
A
C














 

 j
a 2
60
9 s
m
.
c 
         
     i
j
i
i
i
k
i
r
r
k
a
a
a
a
2
2
2
2
2
2
2
60
9
3
3
150
0
8
150
0
20
3
s
m
.
s
m
s
m
m
.
s
rad
m
.
s
rad
s
m
A
D
A
D
A
A
D
A
D














 

    2
2
2
95
12
3
6
12 s
m
.
a
s
m
s
m
. D
D 

 j
i
a

12. Sample Problem
Crank AB of the engine system has a
constant clockwise angular velocity of
2000 rpm.
For the crank position shown,
determine the angular acceleration of
the connecting rod BD and the
acceleration of point D.
SOLUTION:
• The angular acceleration of the
connecting rod BD and the acceleration
of point D will be determined from
• The acceleration of B is determined from
the given rotation speed of AB.
• The directions of the accelerations aD,
(aD/B)t, and (aD/B)n are determined from
the geometry.
• Component equations for acceleration of
point D are solved simultaneously for
acceleration of D and angular
acceleration of the connecting rod.
   n
B
D
t
B
D
B
B
D
B
D a
a
a
a
a
a 





13. Sample Problem
• The acceleration of B is determined from the given
rotation speed of AB.
SOLUTION:
• The angular acceleration of the connecting rod BD
and the acceleration of point D will be determined
from
   n
B
D
t
B
D
B
B
D
B
D a
a
a
a
a
a 




   2
2
2
6
3288
4
209
075
0
0
4
209
2000
s
m
.
s
rad
.
m
.
rω
a
const
s
rad
.
rpm
ω
AB
B
AB
AB








  
j
i
a 



 40
sin
40
cos
6
.
3288 2
s
m
B
 
j
i
a 9
.
2113
2
.
2519 


B

14. Sample Problem
• The directions of the accelerations aD, (aD/B)t, and (aD/B)n are determined from the
geometry.
From Sample Problem 15.3, wBD = 61.98 rad/s, b = 13.95o
.
       2
2
2
3
.
768
98
.
61
2
.
0 s
m
s
rad
m
BD
a BD
n
B
D 

 
    
j
i
a 



 95
.
13
sin
95
.
13
cos
3
.
768 2
s
m
n
B
D
      BD
BD
BD
t
B
D α
.
α
m
α
BD
a 2
0
2
.
0 


The direction of (aD/B)t is known but the sense is not known,
    
j
i
a 


 05
76
05
76
2
0 .
sin
.
cos
. BD
t
B
D 
i
a D
D a


15. Sample Problem
• Component equations for acceleration of point D are solved
simultaneously.
x components:






 95
.
13
sin
2
.
0
95
.
13
cos
3
.
768
40
cos
6
.
3288 BD
o
D
a 





 95
.
13
cos
2
.
0
95
.
13
sin
3
.
768
40
sin
6
.
3288
0 BD
o

y components:
 
 i
a
k
α
2
2
2778
9900
s
m
s
rad
D
BD



   n
B
D
t
B
D
B
B
D
B
D a
a
a
a
a
a 





16. Sample Problem
In the position shown, crank AB has a
constant angular velocity w1 = 20
rad/s counterclockwise.
Determine the angular velocities and
angular accelerations of the
connecting rod BD and crank DE.
SOLUTION:
• The angular velocities are
determined by simultaneously
solving the component equations
for
B
D
B
D v
v
v 

• The angular accelerations are
determined by simultaneously
solving the component equations for
B
D
B
D a
a
a 


17. Sample Problem
SOLUTION:
• Velocity of point D can be obtained from the
expressions,
B
D
B
D v
v
v 

 
j
i
j
i
k
r
ω
v
DE
DE
DE
E
/
D
DE
D



42
42
42
42









 
i
j
j
i
k
r
ω
v
700
400
35
20
20






 A
/
B
AB
B
 
j
i
j
i
k
r
ω
v
BD
BD
BD
B
D
BD
B
D



30
7
7
30








BD
DE 
 7
700
42 



BD
DE 
 30
400
42 



   k
ω
k
ω s
rad
s
rad DE
BD 71
.
11
3
7
.
29 


   
j
i
j
i
j
i BD
BD
DE
DE 


 30
7
400
700
42
42 







E
/
D
DE
D r
ω
v 


18. Sample Problem
Similar to the velocity case consider the two
expressions for the acceleration of point D,
     
j
i
j
i
j
i
j
i
k
r
r
α
a
5740
5740
42
42
42
42
71
11
42
42
2
2















DE
DE
DE
D
DE
D
DE
D
.




   
j
i
j
0i
r
r
α
a
14000
8000
35
2
20
0
2
2








 B
AB
B
AB
B 
     
j
i
j
i
j
i
j
0i
k
r
r
α
a
6160
26400
30
7
7
30
73
29
7
3
2
2













D
B
D
B
D
B
D
B
BD
D
B
BD
B
D
.




x components: 40140
7
42 


 BD
DE 

y components: 14420
30
42 


 BD
DE 

   k
α
k
α 2
2
840
695 s
rad
s
rad DE
BD 


B
D
B
D a
a
a 
 D
DE
D
DE
D r
r
α
a 2





19. Sample Problem
The crane rotates with a constant
angular velocity w1 = 0.30 rad/s and
the boom is being raised with a
constant angular velocity w2 = 0.50
rad/s relative to the cab. The length
of the boom is lOP = 12 m.
Determine:
• angular velocity of the boom,
• angular acceleration of the boom,
• velocity of the boom tip, and
• acceleration of the boom tip.
• Angular acceleration of the boom,
 
2
1
2
2
2
2
1
ω
ω
ω
Ω
ω
ω
ω
ω
α














 Oxyz
• Velocity of boom tip,
r
ω
v 

• Acceleration of boom tip,
  v
ω
r
α
r
ω
ω
r
α
a 








SOLUTION:
With
• Angular velocity of the boom,
2
1 ω
ω
ω 

 
j
i
j
i
r
k
ω
j
ω
6
39
10
30
30
12
50
0
30
0 2
1








.
sin
cos
.
.

20. Sample Problem
j
i
r
k
ω
j
ω
6
39
10
50
0
30
0 2
1




.
.
.
SOLUTION:
• Angular velocity of the boom,
   k
j
ω s
rad
.
s
rad
. 50
0
30
0 

• Angular acceleration of the boom,
 
   k
j
ω
ω
ω
Ω
ω
ω
ω
ω
α
s
rad
.
s
rad
.
Oxyz
50
0
30
0
2
1
2
2
2
2
1









 



 i
α 2
15
0 s
rad
.

• Velocity of boom tip,
0
6
39
10
5
0
3
0
0
.
.
.
k
j
i
r
ω
v 


     k
j
i
v s
m
.
s
m
.
s
m
. 12
3
20
5
54
3 



2
1 ω
ω
ω 


21. Sample Problem
• Acceleration of boom tip,
 
k
j
i
i
k
k
j
i
k
j
i
a
v
ω
r
α
r
ω
ω
r
α
a
90
0
50
1
60
2
94
0
90
0
12
3
20
5
3
50
0
30
0
0
0
6
39
10
0
0
15
0
.
.
.
.
.
.
.
.
.
.
.


















     k
j
i
a 2
2
2
80
1
50
1
54
3 s
m
.
s
m
.
s
m
. 



j
i
r
k
ω
j
ω
6
39
10
50
0
30
0 2
1




.
.
.

22. Sample Problem
For the disk mounted on the arm, the
indicated angular rotation rates are
constant. Determine:
•the velocity of the point P,
•the acceleration of P, and
•angular velocity and angular
acceleration of the disk.
SOLUTION:
• Define a fixed reference frame OXYZ at O
and a moving reference frame Axyz or F
attached to the arm at A.
• With P′ of the moving reference frame
coinciding with P, the velocity of the
point P is found from
F
P
P
P v
v
v 
 
• The acceleration of P is found from
c
F
P
P
P a
a
a
a 

 
• The angular velocity and angular
acceleration of the disk are
  ω
Ω
ω
α
ω
Ω
ω
F
F






D

23. Sample Problem
SOLUTION:
• Define a fixed reference frame OXYZ at O
and a moving reference frame Axyz or F
attached to the arm at A.
j
Ω
j
i
r
1



 R
L
k
ω
j
r
F 2



D
A
P R
• With P’ of the moving reference frame
coinciding with P, the velocity of the point P
is found from
 
i
j
k
r
ω
v
k
j
i
j
r
Ω
v
v
v
v
F
F
F
R
R
L
R
L
A
P
D
P
P
P
P
P
2
2
1
1





















k
i
v L
R
P 1
2 
 



24. Sample Problem
• The acceleration of P is found from
c
P
P
P a
a
a
a F 

 
    i
k
j
r
Ω
Ω
a L
L
P
2
1
1
1 

 








 
  j
i
k
r
ω
ω
a F
F
F
R
R
A
P
D
D
P
2
2
2
2 

 







  k
i
j
v
Ω
a F
R
R
P
c
2
1
2
1 2
2
2



 





k
j
i
a R
R
L
P 2
1
2
2
2
1 2 


 



• Angular velocity and acceleration of the disk,
F
ω
Ω
ω D

 k
j
ω 2
1 
 

 
 
k
j
j
ω
Ω
ω
α F
2
1
1 

 




 
i
α 2
1



27. At a given instant, the gear racks have the
velocities and accelerations as shown.
Determine (a) the angular velocity and
angular acceleration of the gear A and (b)
acceleration of the center of the gear A and the
point B on the perimeter.