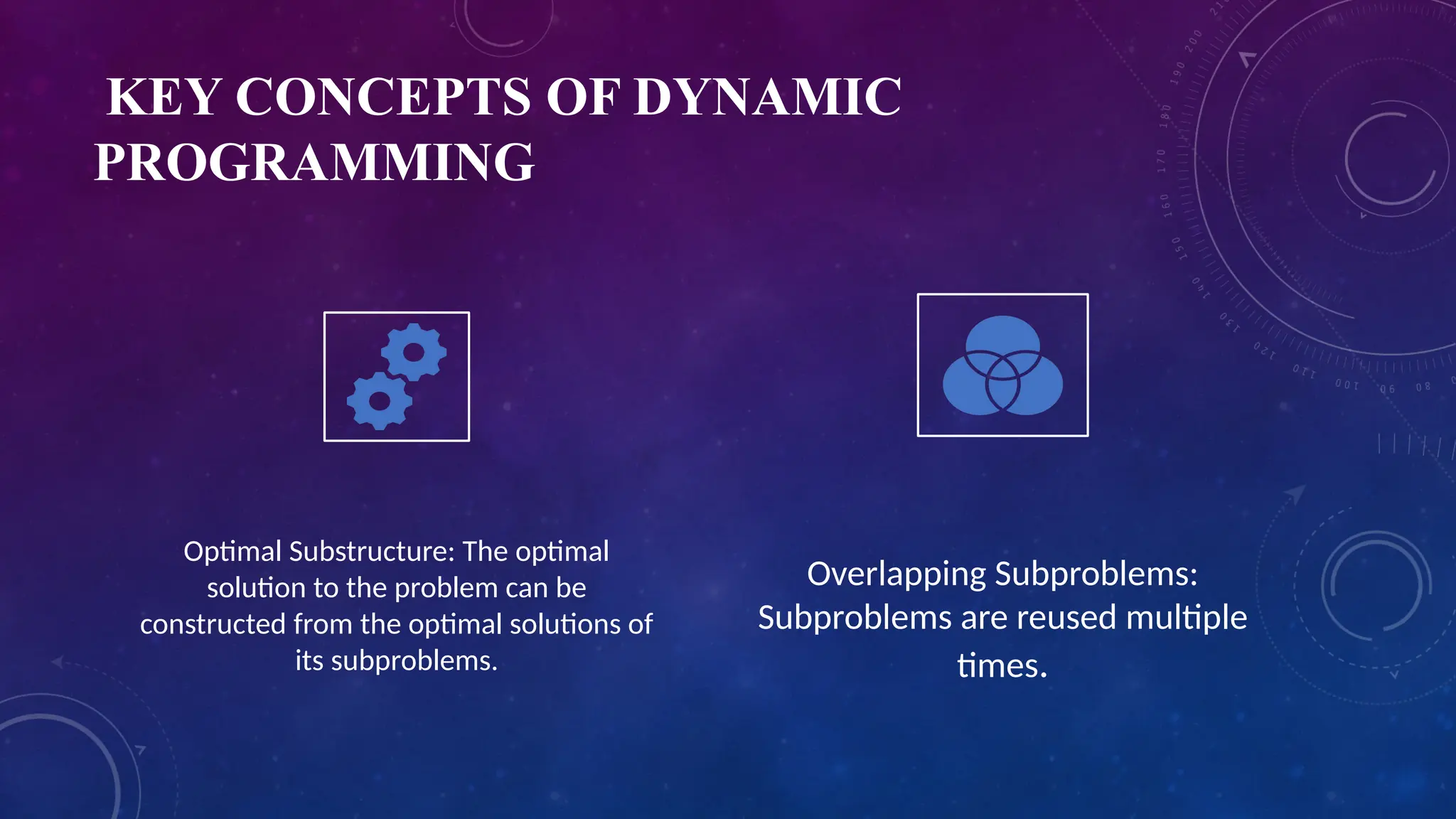
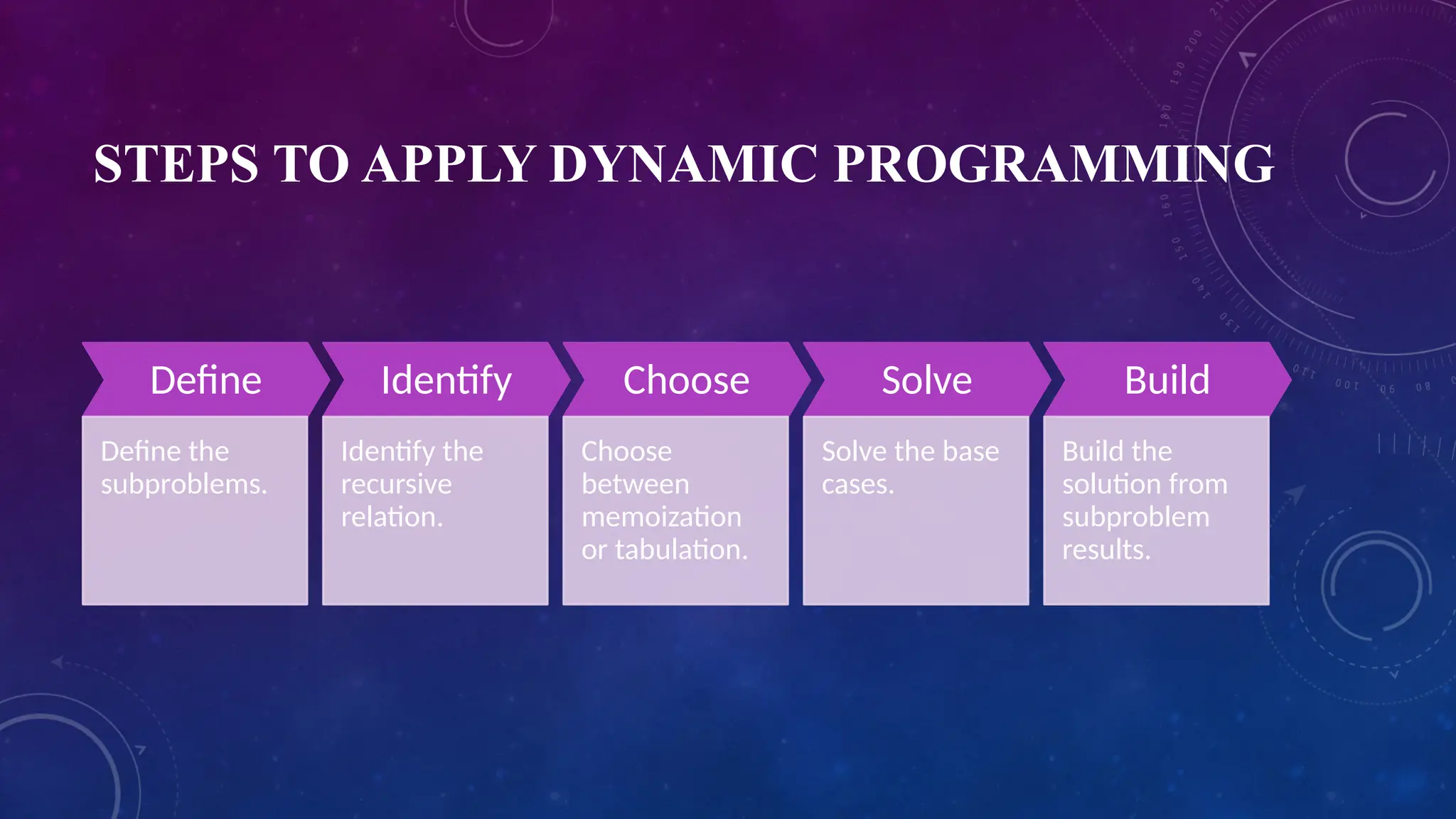
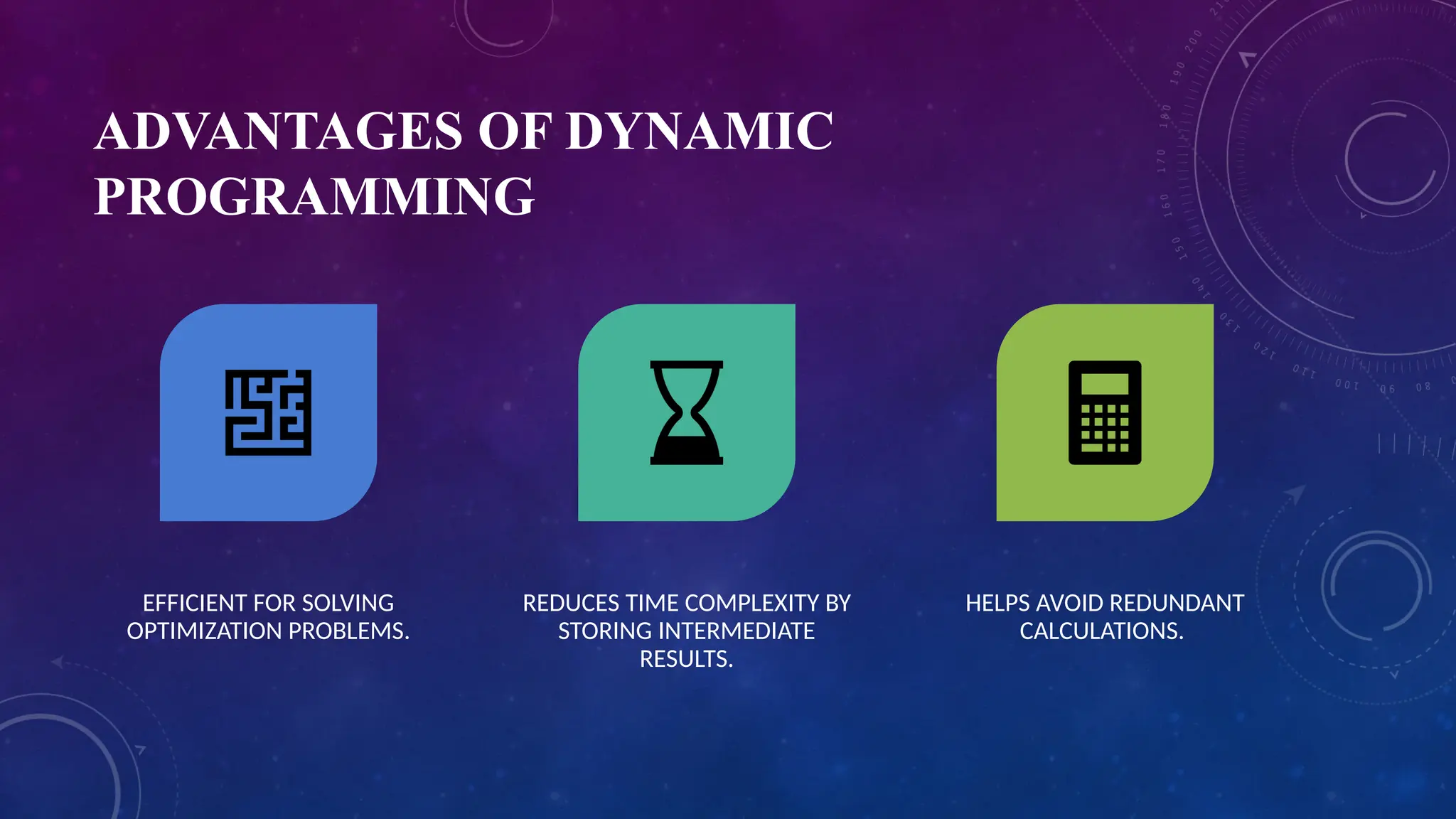
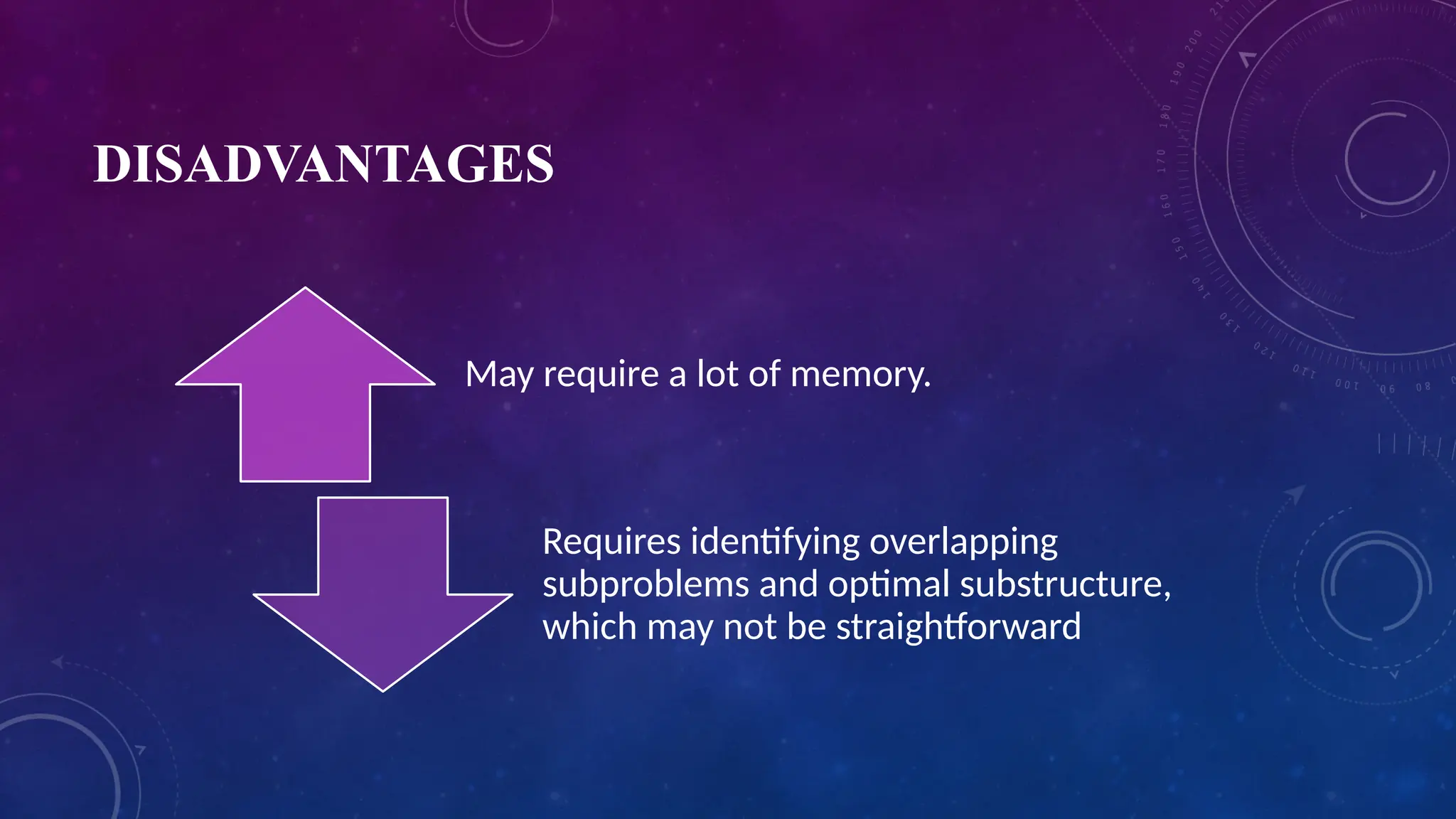
Dynamic programming is a method for solving complex problems by breaking them down into simpler overlapping subproblems with optimal substructure. It is often preferred over greedy methods for optimization problems due to its efficient use of previously solved subproblems through approaches like memoization (top-down) and tabulation (bottom-up). While it can reduce time complexity and avoid redundant calculations, dynamic programming may require significant memory and necessitates the identification of suitable subproblems.

1. DYNAMIC PROGRAMMING
•Presented By Group : 4
•Group Members :
•Md.Nazmus Shakib -220320852
•Tanvin Sadik Dhrubo -220320860
•Khan Waziur Rahman -220320861
•Arghya Saha -200120456

2. INTRODUCTION TO
DYNAMIC PROGRAMMING
• Dynamic Programming is a method for
solving complex problems by breaking
them down into simpler sub problems. It is
applicable where the problem can be
divided into overlapping subproblems and
has optimal substructure. It is also known
as divide and conquer technique

3. Why We Choose Dynamic Programming Over Greedy
Method?
Dynamic programming (DP) is often preferred over the greedy method for solving
optimization problems where future decisions are affected by earlier ones. In
greedy algorithms, the approach is to make the locally optimal choice at each stage
in hopes of finding the global optimum. However, this doesn't always lead to the
best solution for all problems, as greedy methods may miss key subproblems or fail
to consider how earlier decisions affect the later ones.

4. DYNAMIC
PROGRAMMING
APPROACHES
Top Down(Memoization):
Starts By Solving Main Problems & Breaks It
down Into Smaller Parts
Saves The Answers To These Smaller Parts In A
Table To Avoid Doing The Same Work Twice
Works Well When There Are Smaller Parts

5. DYNAMIC PROGRAMMING APPROACHES
Bottom-Up(Tabulation):
Begins by solving the smallest parts of the problem first
Uses these small solutions to build up the final answer step by step
Works well when there are fewer smaller parts,& the final answer can be easily
found by using these smaller solutions

6. MEMOIZATION VS TABULATION
Memoization:Top-
down approach.
Uses recursion.
Stores results of
subproblems as
they are solved
Tabulation:Bottom-
up approach.
Iterative solution.
Builds solutions to
all subproblems and
uses them

7. MEMOIZATION
F4
F2
F1 F0
F1 F1 F0
F2
F3
0 1 1 2 3
F0 F1 F2 F3 F4
F =
Time Complexity= O(n)
Fn
F(n-2)
F(n-1)
Global Array

8. MEMOIZATION
The Fibonacci sequence is defined as:
F(n)=F(n−1)+F(n−2)
with base cases:
F(0)=0, F(1)=1
Function Of fibonacci series :
int fib(int n){
if (n<=1) {
return n;
} else {
return fib(n-2) + fib(n-
1);
}
Top-down approach

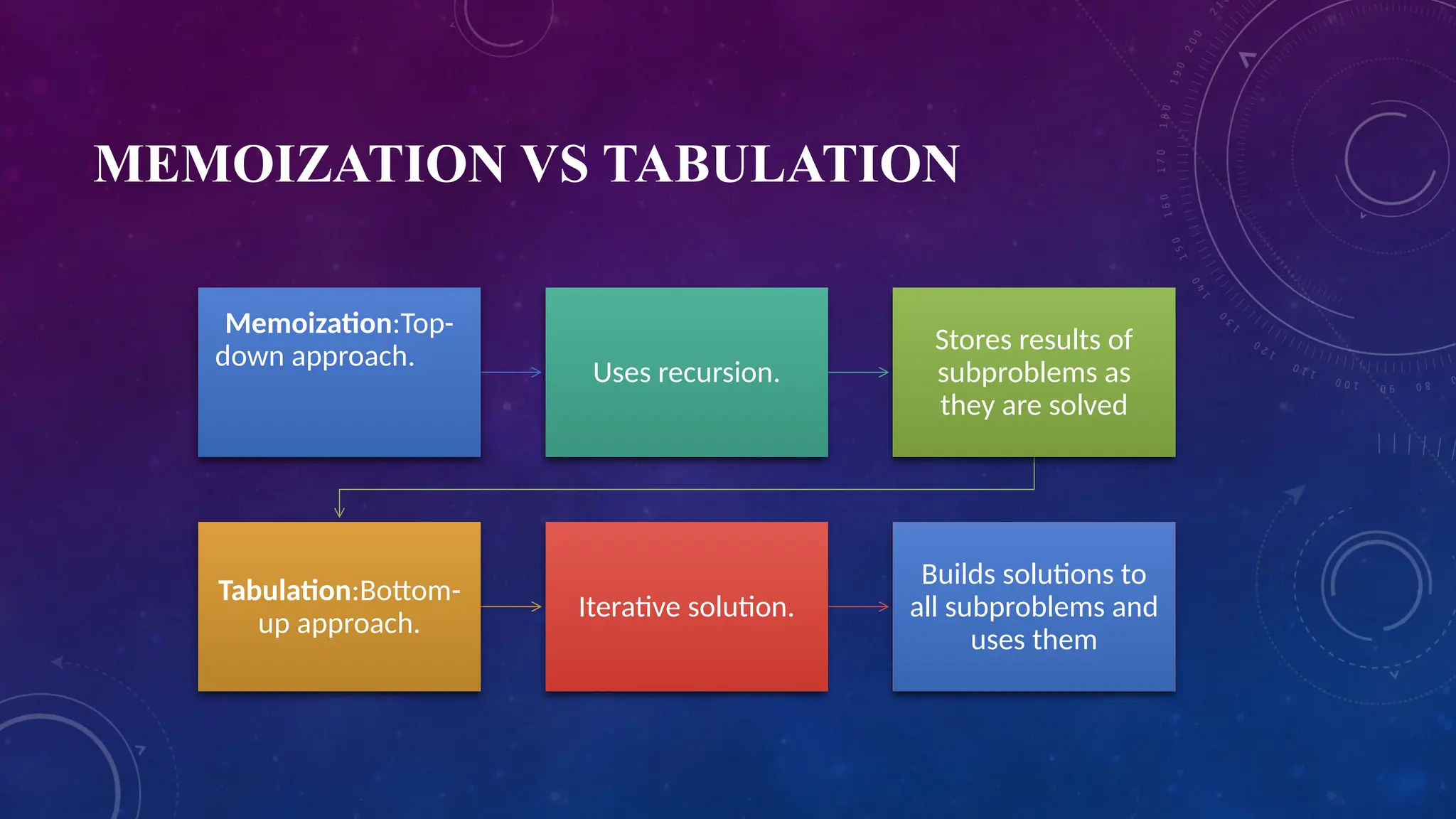
9. TABULATION
Function Of fibonacci series:
int fib(int n){
if (n<=1) {
return n;
F[0]=0;F[1]=1;
}
for(int i=2; i<=n; i++){
F[i] = F[i-2]+F[i-1];
}
return F[n];
}
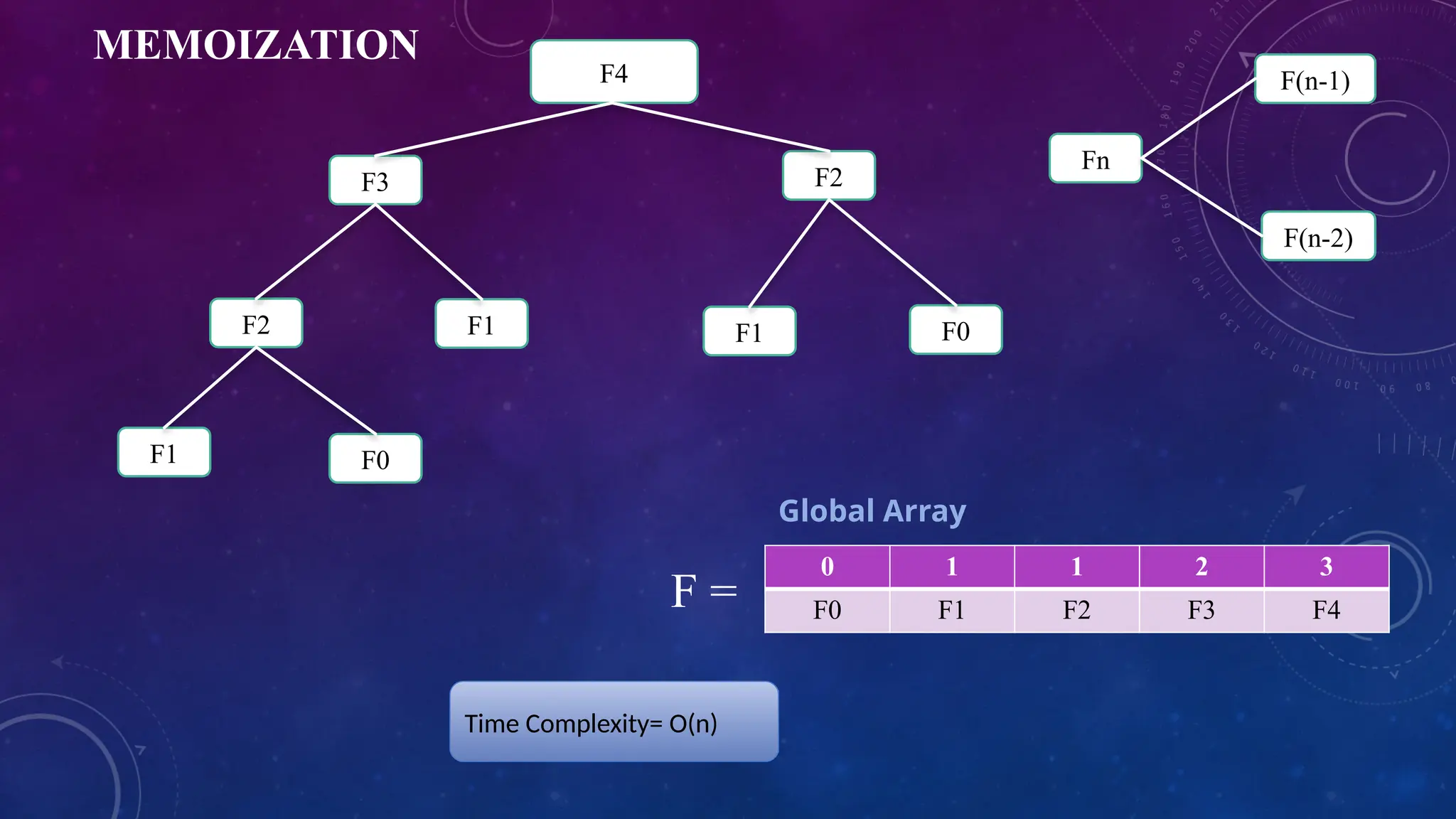
0 1 1 2 3
F0 F1 F2 F3 F4
F =
Time Complexity= O(n)
Global Array
Bottom-up
approach
F1 F0
F2

10. KEY CONCEPTS OF DYNAMIC
PROGRAMMING
Optimal Substructure: The optimal
solution to the problem can be
constructed from the optimal solutions of
its subproblems.
Overlapping Subproblems:
Subproblems are reused multiple
times.

11. STEPS TO APPLY DYNAMIC PROGRAMMING
Define
Define the
subproblems.
Identify
Identify the
recursive
relation.
Choose
Choose
between
memoization
or tabulation.
Solve
Solve the base
cases.
Build
Build the
solution from
subproblem
results.

12. ADVANTAGES OF DYNAMIC
PROGRAMMING
EFFICIENT FOR SOLVING
OPTIMIZATION PROBLEMS.
REDUCES TIME COMPLEXITY BY
STORING INTERMEDIATE
RESULTS.
HELPS AVOID REDUNDANT
CALCULATIONS.

13. DISADVANTAGES
May require a lot of memory.
Requires identifying overlapping
subproblems and optimal substructure,
which may not be straightforward

14. THANK YOU!