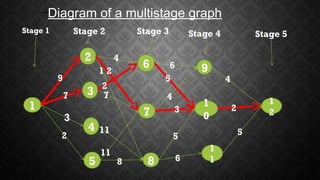
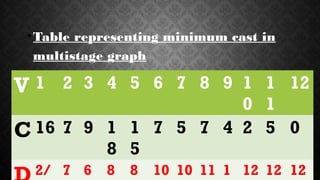
Dynamic programming is an algorithm design technique for solving complex problems defined by overlapping subproblems. It works by solving each subproblem only once and storing the results for future use, avoiding the work of recomputing results. The principle of optimality states that optimal solutions can be constructed from optimal solutions of subproblems. Dynamic programming algorithms involve characterizing the optimal substructure, recursively defining the optimal value, computing the optimal value in a bottom-up manner, and constructing an optimal solution. It is generally applied to optimization problems and provides efficient solutions, though it may not always find a global optimum. An example is finding the minimum cost path through a multistage graph.

1. PRESENTATION Topic : “DYNAMIC PROGRAMMING”
Prepared By: Pintu Ram
Course: B.Sc.(Hons.)C.S. Sem : 2nd Roll no : 2k17/CS/72
Submitted to : Mr. Ashish Jha
College Of Vocational Studies

2. INDEX
WHAT IS DYNNAMIC PROGRAMMMING
WHAT IS OPTIMIZATION PROBLEM
WHAT IS OPTIMAL SOLUTION
PRICIPLE OF OPTIMALITY
DYNAMIC PROGRAMMING ALGORITHM
ADVANTAGE OF DYNAMIC PROGRAMMING
DISADVANTAGE OF DYNAMIC
PROGRAMMING
EXAMPLE OF DYNAMIC PROGRAMMING

3. WHAT IS DYNAMIC PROGARMMING
DEFINITION:
Dynamic Programming is a general algorithm
design technique for solving a complicated
problem defined by recurrences with overlapping
sub problems.
Invented by : “American mathematician”
“Richard Bellman”
in 1950

4. Dp and dcp
DP:> Dynamic Programming
DCP:> Divide and Conquer Programming
DP likes DCP.
But, Some difference
DCP :applies when sub problems does not overlap.
(repeatedly works)/(top down)
DP :applies when sub problems overlap.
(avoids repeatedly works)(bottom up)

5. Optimization problem
Dynamic Programming is generally applied for
solving optimization problems.
OPTIMIZATION PROBLEM:
Such problems that can have many possible
solutions and each solution has a
value and we wish to find a solution with
optimal value (minimum and maximum).

6. Optimal solution
It is a feasible/suitable/appropriate/right
solution which is our favorable.
Or not a solution but the best solution.
It provides the most beneficial result for the
specified objective problems.
If the objective problem is related to profit then
optimal solution has a maximum value
While if the objective problem is related to the
cost the optimal solution has a minimum value.

7. Principle of optimality
The Dynamic Programming works on a
principle of optimality.
“The principle of optimality states that in an
optimal sequences of decisions/choices, each
sequences must also be optimal.”

8. Dynamic programming algo
or dpa
Steps for designing a DPA:
♠CHRACTERIZE optimal substructure.
♠RECURSIVELY define the. optimal value
♠COMPUTE the optimal value in bottom up.
♠CONSTRUCT an optimal solution.

9. ADVANTAGE OF DYNAMIC PROGRAMMING
Easier to implement.
Require much less computing resources.
Much faster to executer.
Greedy algorithm is used to solve optimization
problems.

10. DISADVANTAGE OF DYNAMIC
PROGRAMMING
It does not always reach to the global solution.
Or,
Even the global solution is not found, most of
the times is lose, and in this case the sub
optimal solution is the best solution.

11. EXAMPLE OF DYNAIMC PROGRAMMING
Multi graph:
A multistage graph is a directed weighted graph
and the vertices are divided into stages such that
the edges are connecting the vertices from one
stage to next stage only. First stage and last stage
have a single vertex to represent the starting
point to sink of a graph.

12. Objective of problem
We have to selecting the path which
is giving us the minimum cost.

13. –Diagram of a multistage graph
–
1
2
1
2
1
1
1
0
9
5
4
3
8
7
6
9
6
4
2
5
68
2
7
3
21
2
7
11
11
5
4
5
3
Stage 1 Stage 2 Stage 3 Stage 4 Stage 5
4

14. Finding the cost of each stages and vertices are
following:
Cost (5,12)=0 | Cost (4,9)=4 | Cost (4,9)=2 | Cost
(4,11)=5
Cost (3,6)=min { cost(6,9)+cost(4,9),
cost(6,10)+cost(4,10) }
=min{ 6+4 , 5+2 }
=7
Similarly:
Cost(3,7)=5 | Cost(3,8)=7 | Cost(2,2)=7 | Cost(2,3)=9 |
Cost(2,4)=18 | Cost(2,5)=15 | Cost(1,1)=16

15. •Table representing minimum cast in
multistage graph
V 1 2 3 4 5 6 7 8 9 1
0
1
1
12
C 16 7 9 1
8
1
5
7 5 7 4 2 5 0
2/ 7 6 8 8 10 10 11 1 12 12 12

16. Formulation for finding the minimum cast in
multistage graph.
cost(i , j) = min{cost(j , l)+cost(i+1 , l)}
(j, l) € edges
l € s+1 (next stage)
stage vertex next stage

17. Thank you