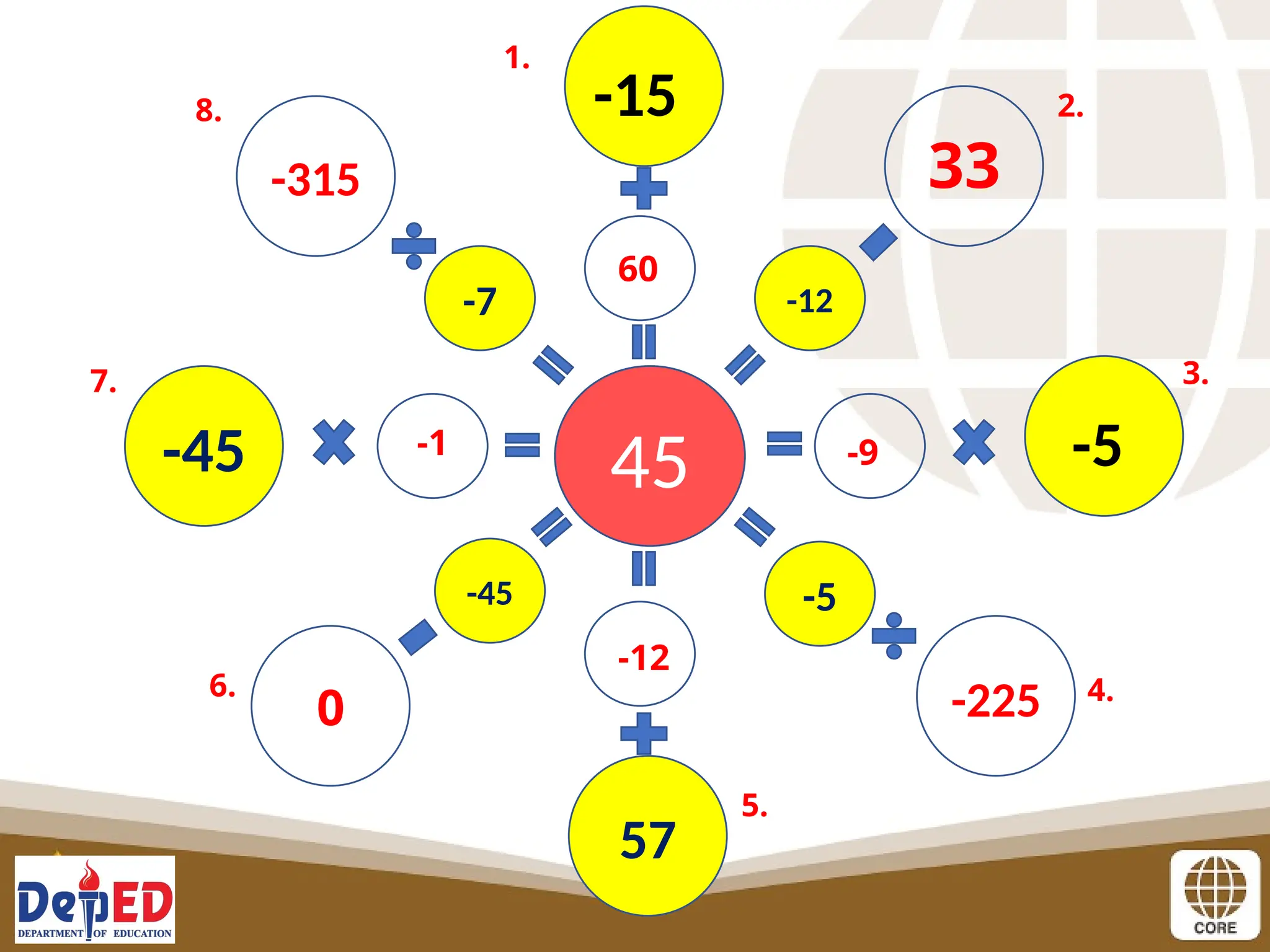
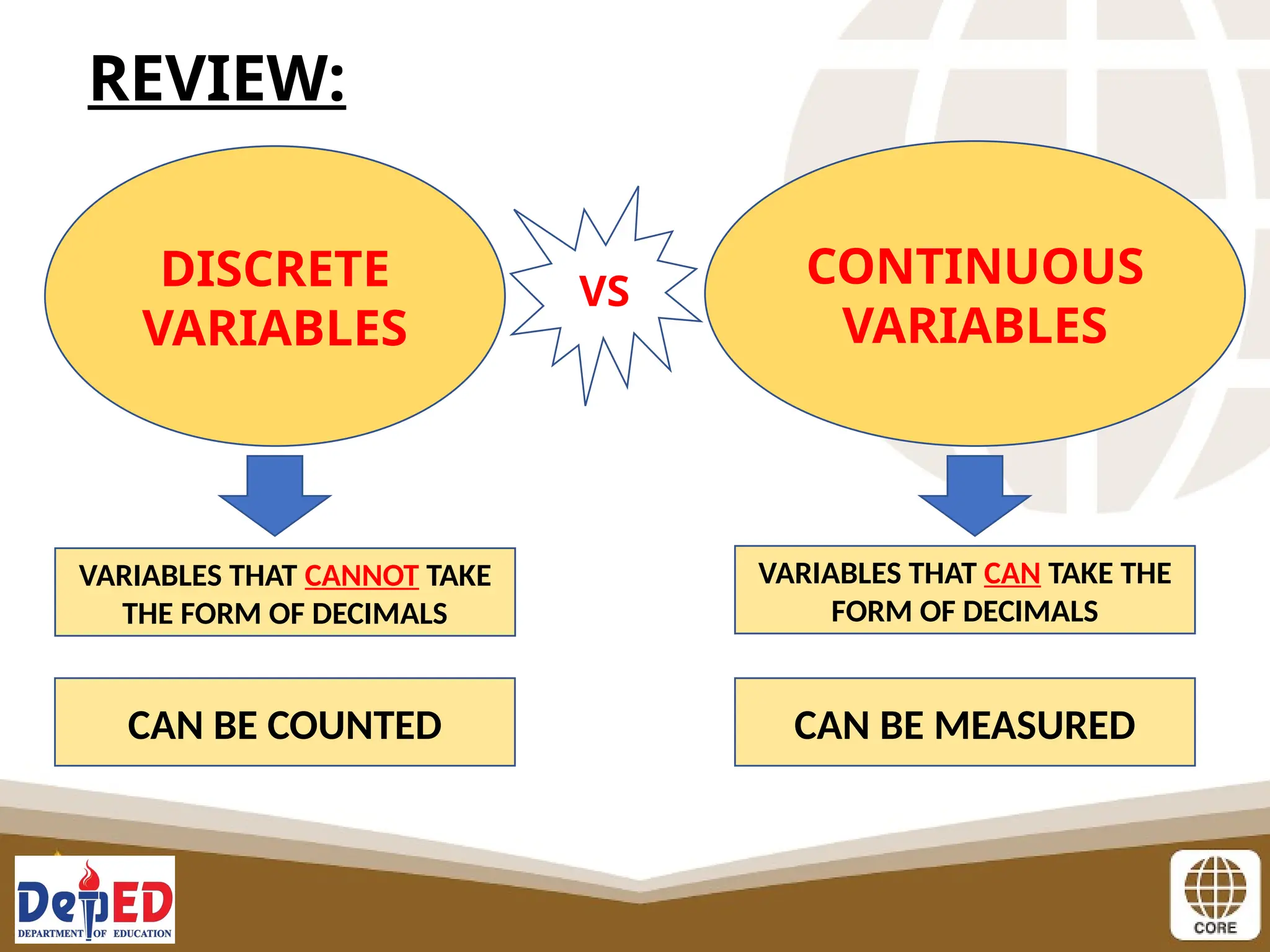
The document outlines a lesson plan for a senior high school mathematics class focusing on probability distributions for discrete random variables. It includes preliminary activities such as an opening prayer, attendance check, and math puzzles, followed by lesson objectives and various experiments designed to teach students how to compute and understand probability distributions. The lesson concludes with assessments and assignments aimed at reinforcing the concepts learned.

1. GENERAL MATHEMATICS
for SENIOR HIGH SCHOOL

2. Preliminary Activities
1. Opening Prayer

3. Opening Prayer
Heavenly Father and Your Beloved Son Jesus Christ,
Thank you for another day of being able to go to school and
learn new set of things we will experience in our classes today.
As we go through our class at this moment, give us wisdom to
understand the lessons that we will be discussing this afternoon.
Help us to be obedient, honest, and kind to one another. Bless
our teachers, our school and my fellow students.
In Jesus’ name we pray. Amen.

4. 2. Checking of Attendance

5. 3. Preliminary Activities
Math Puzzle

6. 45
-12
-7
-45 -5
57
-45
-15
-5
1.
2.
3.
4.
5.
6.
7.
8.
60
33
-9
-225
-12
0
-1
-315

8. LESSON OBJECTIVES:
At the end of the period, the students with 80%
accuracy,
are expected to:
• Know what is a probability distribution for a discrete
random variable and its properties;
• compute probabilities corresponding to a given random
variable; and
• construct the probability mass function of a discrete
random variable

9. REVIEW:
DISCRETE
VARIABLES
CONTINUOUS
VARIABLES
VS

10. REVIEW:
DISCRETE
VARIABLES
CONTINUOUS
VARIABLES
VS
VARIABLES THAT CANNOT TAKE
THE FORM OF DECIMALS
CAN BE COUNTED
VARIABLES THAT CAN TAKE THE
FORM OF DECIMALS
CAN BE MEASURED

11. REVIEW:
DISCRETE
VARIABLES
CONTINUOUS
VARIABLES
VS
VARIABLES THAT CANNOT TAKE
THE FORM OF DECIMALS
CAN BE COUNTED
VARIABLES THAT CAN TAKE THE
FORM OF DECIMALS
CAN BE MEASURED

12. REVIEW:
Which of the following statements is considered a DISCRETE or
CONTINUOUS data.
1. The harvest package received second week was 4.3 kilos.
2. The maximum temperature in Metro Manila on Jan. 21,2018
according to the weather newscaster was 34.2 degree Celcius
3. In the City of Cebu, a total of 25 fires were reported by the
Cebu City Fire Department to have occurred during the year
2015.
4. Dr. Cano’s reported income for the past year was P530,855.43
per annum.
5. Only 345 applicants passed the College of Education Entrance
Test in Cebu Normal University

13. REVIEW:
FINDING POSSIBLE VALUES OF RANDOM VARIABLES:
STEPS:
1. To determine the sample space/number
possible outcome, use where n is refers to
number of an object.
2. Make a table.
3. Identify the possible values of the random
variable.

14. Decision-making is an important aspect in business, education,
insurance, and other real-life situations. Many decisions are
made by assigning probabilities to all possible outcomes
pertaining to the situation and then evaluating the results.
For instance, an insurance company might be able to assign
probabilities to the number of vehicles a family owns. This
information will help the company in making decisions
regarding future financial situations. This situation requires the
use of random variables and probability distribution.
Ask: How does probability distribution relates to real-life
situation?
Lesson Introduction:

15. DISCUSSION ON
DISCRETE PROBABILITY
DISTRIBUTION

16. DISCRETE PROBABILITY
DISTRIBUTION
Also known as probability mass
function consists of the values of
random variable can assume
and the corresponding probabilities
of the values.

17. DISCRETE PROBABILITY
DISTRIBUTION
Properties:
1. The probability of each value of the random
variable must be between or equal to 0 and 1.
2. The sum of the probability of all values of the
random variable must be equal to 1

18. Illustrative Example:
Finding the probability corresponding to a given random variable
Experiment #1: Drawing balls from a basket
Two balls are drawn in succession without
replacements from a basket, contains 4 yellow
balls and 4 blue balls. Let X be the random
variable representing the number of blue balls,
Find the values of the random variable X.

19. • Step 1: Determine the sample space
• Step 2: List the possible outcome
• Step 3: Count the number of the variable asked
in the experiment in each outcome in the sample
space and assign this number to this outcome
Finally,
• Given the values of the possible outcomes,
solve/compute the probability P of each value of
the random variable.
Discussion Points:

20. The Probability Distribution or the Probability
Mass Function of Discrete Random Variable Z
Solution to Experiment #1

21. Group Activity
Finding the probability corresponding to a given random variable
Experiment # 2: Tossing Three Coins
Suppose three coins are tossed. Let Y be the
random variable representing the number of
tails that occur. Find the probability of each of
the values of the random variable Y.

22. Group Activity
Finding the probability corresponding to a given random variable
Experiment # 3: Defective Cellphones
Suppose three cell phones are tested at random. We
want to find out the number of defective cell phones
that occur. Let D represent the defective cellphone
and N represent the non-defective cellphone. Let X
be the random variable representing the number of
defective cellphones. Construct the probability
distribution of the random variable X.

23. Solution to Experiment # 2
Probability Distribution or Probability Mass
function of Discrete Random Variable X
Continuation Step 3

24. A discrete probability distribution or a
probability mass function consists of the
values a random variable can assume and the
corresponding probabilities of the values.
Summary:

25. Properties of a Probability Distribution
•The probability of each value of the random
variable must be between or equal to 0 and
1. In symbol, we write it as 0 P(X) 1.
≤ ≤
•The sum of the probabilities of all values of
the random variable must be equal to 1. In
symbol, we write it as P(X) = 1.
∑
Summary:

26. • Step 1: Determine the sample space
• Step 2: List the possible outcome
• Step 3: Count the number of the variable asked
in the experiment in each outcome in the sample
space and assign this number to this outcome
Finally,
• Given the values of the possible outcomes,
solve/compute the probability P of each value of
the random variable.
Summary:

27. Assessment
•The students will answer Worksheet 3.4
•Checking of answers will follow.
•Feedbacking of results and difficulties

28. Assignment
•The students will answer Activity 3.2 and
Activity 3.3 pages 14 and 15 in their
Module.
•To be submitted next meeting

29. THOUGHTS TO PONDER:

30. End Activity
Closing Prayer