The document describes a study that tested Miller's hypothesis about short-term memory capacity and chunking. It presented subjects with digit sets of varying lengths (3, 5, 7, or 9 digits) in either serial or sequential order. Recall accuracy declined significantly as digit set length increased but order had no effect, failing to support chunking. The study was limited by its small sample size of two. It did not provide clear evidence for Miller's "magic number of 7" or demonstrate chunking, but hinted capacity may be closer to Cowan's proposed 4 digits. Further research with varied designs and larger samples is needed to better understand short-term memory limits.

1. Short-Term Memory Test: Digit Span Experiment 1
A Study of Short-Term Memory Capacity Through the Use of a Digit Span Experiment
William Teng
University of California, Irvine
Wteng1@uci.edu

2. Short-Term Memory Test: Digit Span Experiment 2
Abstract
Miller’s hypothesis regarding short-term memory store capacity and chunking during
retention was investigated using a two-factor six level design. Subjects were given sets of digits
varying in three digits, five digits, seven digits, or nine digits in either serial or sequential order.
They were to accurately recall the digit set, to the best of their abilities, after a short study period.
Statistical analysis failed to show a significant effect of order size on recall accuracy, which
would suggest a failure to demonstrate an effect of chunking. Miller’s “magic number” also
failed to gain any significant statistical evidence, however, it did show trends of approaching
significance.
Keywords: Miller, Short-term Memory, Cowan, Memory, Magic Number, Chunking, Digit
Span, Retention, Short-term Memory Capacity

3. Short-Term Memory Test: Digit Span Experiment 3
Introduction
Schweickert and Boruff (1986) explained that short-term memory (STM) store is limited
to a fundamental capacity, but unclear as to how much. In Miller’s (1956) study, he suggested
that this fundamental capacity for accurate STM retention can be expressed by the “magic
number” of seven, plus or minus two, chunks of information. The idea of chunking is essential to
Miller’s hypothesis, however, it was vaguely defined in his work. Further study done by Gobet et
al. (2001) offered a more concrete definition of chunks as, “A collection of elements having
strong associations with one another, but weak associations with elements within other chunks.”
In other words, chunking refers to recoding individual pieces of information into one meaningful
unit. Simon’s (1974) study claimed to have confirmed Miller’s hypothesis and consistently
replicated a capacity of five to seven chunks.
Nonetheless, other studies have challenged Miller’s “magical number” and claimed that
STM capacity is in fact less. Cowan (2001) disagreed with Miller and instead proposed a
capacity of four, plus or minus one. Mathy and Feldman (2012) in their article, What’s Magic
About Magic Numbers? Chunking and Data Compression in Short-Term Memory, came to an
interesting conclusion and stated that STM capacity is three to four distinct chunks, however,
about seven when items are uncompressed.
The purpose of this current study is to confirm Miller’s “magic number” as well as to
demonstrate an effect of chunking on STM retention. To do so, the experiment will be conducted
using a two-factors, six-levels digit span task. The “magic number” will be tested through
varying number of digits presented at each level, whereas, chunking will be demonstrated
through presenting the digits in either serial or sequential order. Recall accuracy is expected to

4. Short-Term Memory Test: Digit Span Experiment 4
demonstrate a negative trend as number of digits increase. Accuracy is also expected to be lower
for serial order presentation than that of sequential due to chunking.
Methods
Participants
Participants for this digit span study consisted of a total of two subjects, which included
the author (Senior) and an additional subject (Freshman) recruited from the UCI Psychology
Department Subject Pool. The author was a male enrolled in an upper-division research course,
whereas, the recruited subject was a female in the Psychology Fundamentals course.
Furthermore, the recruited subject stated she has carried out a similar digit span experiment in a
previous high school psychology class.
Materials
This digit span task was performed within the Social Science Laboratories at UCI. Both
subjects carried out the experiment using a computer running the “Matlab 2012B” software. The
stimuli used were randomized sets of numerical digits, which were manipulated based on the
experimental design. After all trials, recorded data were then analyzed using the “IBM SPSS”
statistical software.
Procedure
The experiment was a two-factors, six-levels design, with the factors being order type
and number of digits. Order type varied between two levels, serial (one digit at a time) and
sequential (whole set of digits). The number of digits varied in levels of three, five, seven, or
nine digits. Fixed parameters of exposure time, type of digits, and color were assigned
respectively as three seconds, numerical, and fixed. Subjects interacted only with the “Matlab”
program executing 10 trials for each set of levels. For each trial, subjects were to study a given

5. Short-Term Memory Test: Digit Span Experiment 5
data set and then proceed to recall all digits in correct order. At the end of 10 trials, the number
of correct recalls was recorded before moving onto the next set of levels. The above steps were
repeated for all level pairings until a total of 80 trials were completed. Lastly the percentages of
correct recalls were analyzed through a 2X4 repeated-measures ANOVA test.
Results
Using SPSS, a 2X4 repeated-measures ANOVA failed to display a significant effect of
order type on recall accuracy [F(1,1) = 5.898, p = 0.249], however, it did demonstrate a
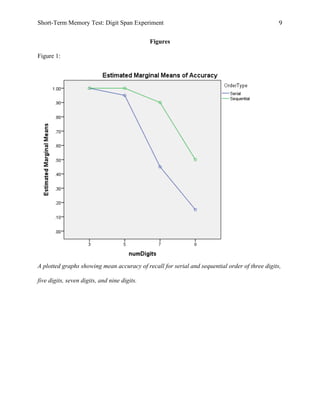
significant effect of number of digits on accuracy [F(3,3) = 9.433, p = 0.049]. Figure 1
illustrates a negative correlation between number of digits and recall accuracy. The same tests
also failed to show any interaction effects between order type and number of digits [F(3,3) =
3.983, p = 0.143].
Within-subjects contrasts failed to reveal a significant difference between serial order
type and sequential order type [F(1,1) = 5.898, p = 0.249]. Furthermore, it also failed to display
significant differences between nine digits versus three digits [F(1,1) = 29.160, p = 0.117], nine
digits versus five digits [F(1,1) = 42.250, p = 0.097], and nine digits versus seven digits [F(1,1) =
12.250, p = 0.177].
Figure 1 appeared to show a large difference in recall accuracy means between
sequential, five digits versus sequential, seven digits. However, a paired samples t-test of the two
means failed to demonstrate any significant difference [t(1) = 1.000, p = 0.500]. Figure 1 also
indicated a difference between serial, seven digits and sequential, seven digits. Further paired
samples t-test failed to confirm any significance [t(1) = -1.800, p = 0.323].

6. Short-Term Memory Test: Digit Span Experiment 6
Discussion
The results of this experiment would suggest that STM retention declines as amount of
information begins approaching the store’s capacity. When asked to complete the digit span
tasks, the number of digits presented showed a statistically significant effect on subjects’ recall
accuracies. As initially predicted, figure 1 displayed a negative relationship between number of
digits and recall accuracy. However, Miller’s (1956) “magic number” of seven, plus or minus
two, was not supported. When each number of digits level was paired against nine digits, there
appeared to not be any significant difference in effect towards recall accuracy. Further analysis
using paired comparisons of accuracy means between five digits and seven digits also failed to
show any significant differences. Despite the finding that recall accuracy decreased as number of
digits increased, an actual threshold for STM capacity could not be accurately determined.
Nonetheless, it is interesting to note that comparison between nine digits and five digits did
display a trend of approaching significance. This could suggest that significance could be
obtained if further testing was conducted. One factor that could have influenced the observed
outcome was the small sample size of this study. Perhaps it would be interesting to study the
same conditions using a larger sample size. Another study of interest may be to test Cowan’s
(2001) newly proposed STM capacity of four, plus or minus one.
Furthermore, order type failed to show any significant effect on recall accuracy. This
indicates that chunking was not utilized during retention. Failure to demonstrate an effect of
chunking could also be attributed to experimental design flaws. Again, the statistics could be an
unfair representation due to a sample size of only two. Another factor that could have had an
effect was digit type. For this particular experiment, only numerical digits were used and perhaps
alphabetical letters could have been used instead to promote chunking. Letters could have

7. Short-Term Memory Test: Digit Span Experiment 7
offered a more intuitive way of chunking since language already requires recoding single letters
into meaningful units.
In conclusion, the true quantity of STM capacity still eludes us after this experiment.
Miller’s “magic number” was not supported and chunking effects failed to be displayed in the
findings. The only conclusive evidence in this study was the significant negative effect of an
increasing number of digits on recall accuracy. Further study regarding STM should be
conducted using varying experimental designs and a larger sample size. As proposed earlier,
using letters instead of numeric digits could help induce chunking. Also perhaps a shift in focus
from Miller’s (1956) seven, plus or minus two, to Cowan’s (2001) four, plus or minus one, could
help better explain STM capacity. Future study could offer a better understanding of the inner-
workings of STM.

8. Short-Term Memory Test: Digit Span Experiment 8
References
Cowan, N. (2001). The magical number 4 in short-term memory: A reconsideration of mental
storage capacity. Behavioral and Brain Sciences, 24(1), 87-185.
Gobet, F., Lane, P. C. R., Croker, S., Cheng, P. C., Jones, G., Oliver, I., & Pine, J. M. (2001).
Chunking mechanisms in human learning. Trends in Cognitive Sciences, 5(6), 236-243.
Mathy, F., & Feldman, J. (2012). What’s magic about magic numbers? chunking and data
compression in short-term memory.Cognition, 122(3), 346-362.
Miller, G. A. (1956). The magical number seve, plus or minus two: Some limits on our capacity
for processing information. Psychological Review, 63, 81-97
Schweickert, R., & Boruff, B. (1986). Short-term memory capacity: Magic number or magic
spell? Journal of Experimental Psychology: Learning, Memory, and Cognition, 12(3),
419-425.
Simon, H. A. (1974). How big is a chunk?. Science, New Series, 183(4124), 282-288.

9. Short-Term Memory Test: Digit Span Experiment 9
Figures
Figure 1:
A plotted graphs showing mean accuracy of recall for serial and sequential order of three digits,
five digits, seven digits, and nine digits.