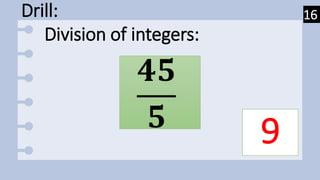
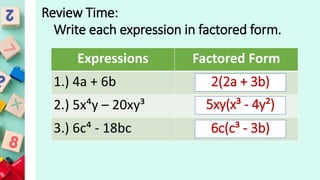
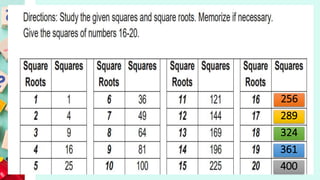
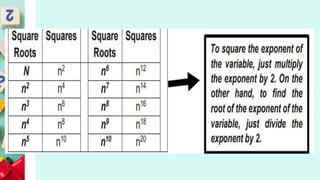
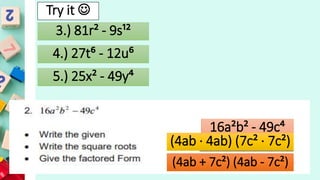
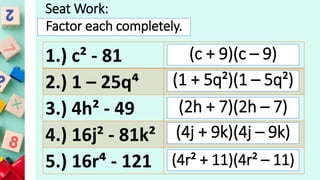
This document provides examples and instructions for adding, subtracting, multiplying, and dividing integers. It also covers factoring expressions using the difference of two squares formula. Some key steps include: for addition and subtraction, keep signs the same for like terms and change signs for unlike terms; for multiplication and division, keep signs the same or change depending on an odd or even number of negatives; and to factor a difference of two squares, factor each term into the product of two binomials and group factors. Practice problems with answers are provided for each concept.

2. Same sign ADD and keep
Different sign SUBTRACT
Take the sign of the bigger number
then it will be exact


3. Drill:
(+5) + (+4)
+9
Addition of integers:
1

4. Drill:
(-5) + (+4)
-1
Addition of integers:
2

5. Drill:
(-10) + (-12)
-22
Addition of integers:
3

6. Drill:
(+7) + (-15)
-8
Addition of integers:
4

7. Drill:
(-2) + (+2)
0
Addition of integers:
5

8. Drill:
(+2) - (+1)
+1
Subtraction of integers:
6

9. Drill:
(+2) - (-3)
+5
Subtraction of integers:
7

10. Drill:
(-1) - (-3)
+2
Subtraction of integers:
8

11. Drill:
(-8) - (-5)
-3
Subtraction of integers:
9

12. Drill:
(-1) - (-1)
0
Subtraction of integers:
10

13. Drill:
5(-2)
-10
Multiplication of integers:
11

14. Drill:
-5(-5)
+25
Multiplication of integers:
12

15. Drill:
-5(7)
-35
Multiplication of integers:
13

16. Drill:
-23(0)
0
Multiplication of integers:
14

17. Drill:
8(6)
48
Multiplication of integers:
15

18. Drill:
𝟒𝟓
𝟓 9
Division of integers:
16

19. Drill:
−𝟏𝟔
𝟒 -4
Division of integers:
17

20. Drill:
−𝟏𝟔
−𝟏𝟔 1
Division of integers:
18

21. Drill:
𝟎
𝟏𝟓 0
Division of integers:
19

22. Drill:
−𝟏𝟖
−𝟐 9
Division of integers:
20

24. Review Time:
Find the factor of 12j⁴ + 18j⁶
Factors of 12 are 1, 2, 3, 4, 6, 12
Factors of 18 are 1, 2, 3, 6, 9, 18
CMF = 6j⁴ 12j⁴
6j⁴
+
18j⁶
6j⁴
6j⁴ (2 + 3j²)
6j⁴ (2 + 3j²)

25. Expressions Factored Form
1.) 4a + 6b
2.) 5x⁴y – 20xy³
3.) 6c⁴ - 18bc
Review Time:
Write each expression in factored form.
2(2a + 3b)
5xy(x³ - 4y²)
6c(c³ - 3b)

26. Difference of Two Squares
Objectives for today;
1. Factor the difference of two squares.
2. Enjoy while learning

27. 256
289
324
361
400

29. For a binomial to be a difference of two
squares, two condition must hold.
 There must be two terms that are
both squares. Examples are 9a² and
25a⁴ and 81 and x².
 There must be a minus sign
between two terms.

30. Are the first term & second term
the same? Why or why not?

31. What pattern is seen in the factors of
difference of two squares?

32. When can you factor expressions
using difference of two squares?

33. Can all expressions be factored
using difference of two squares?
Why or why not?

34. 16a²b² - 49c⁴
(4ab · 4ab) (7c² · 7c²)
(4ab + 7c²) (4ab - 7c²)

35. 16a²b² - 49c⁴
(4ab · 4ab) (7c² · 7c²)
(4ab + 7c²) (4ab - 7c²)
3.) 81r² - 9s¹²
4.) 27t⁶ - 12u⁶
5.) 25x² - 49y⁴
Try it 

36. Real life application:
Write a polynomial for the area of the shaded
region, then factor completely.
x
7x
4
7

37. x
7x
4
7
Find the area of
the larger
rectangle:
Find the area of
the smaller
rectangle:
A = lw
= 7x(x)
= 7x²
A = lw
= 7(4)
= 28
Polynomial: 7x² - 28
Factor: 7x² - 28 GCF: 7
7x² - 28 = 7 (x² - 4)
= 7 (x + 2) (x – 2)

38. Generalization:
1. How do you find the factors of difference
of two squares?
2. Why is it important to learn the squares
and square roots of the number?
3. Is it possible to factor an expression if it
contains a number that is not a square? Depend
your answer.

39. 1.) c² - 81
2.) 1 – 25q⁴
3.) 4h² - 49
4.) 16j² - 81k²
5.) 16r⁴ - 121
Seat Work:
Factor each completely.
(c + 9)(c – 9)
(1 + 5q²)(1 – 5q²)
(2h + 7)(2h – 7)
(4j + 9k)(4j – 9k)
(4r² + 11)(4r² – 11)