This document discusses Dialectica categories and cardinalities of the continuum. It begins by outlining Hilbert's program to provide secure foundations for mathematics through formalization. Gödel's incompleteness theorems showed this was impossible. Gödel then developed the Dialectica interpretation as a way to prove consistency of arithmetic. De Paiva later introduced Dialectica categories, which provide a model of linear logic. These categories, called PV, are useful for proving inequalities between cardinal characteristics of the continuum. The structure of PV is discussed, along with examples of objects in this category.

![Introduction
Introduction
[...]It often happens that there are similarities between the
solutions to problems, or between the structures that are thrown
up as part of the solutions. Sometimes, these similarities point to
more general phenomena that simultaneously explain several
different pieces of mathematics. These more general phenomena
can be very difficult to discover, but when they are discovered,
they have a very important simplifying and organizing role, and
can lead to the solutions of further problems, or raise new and
fascinating questions.
– T. Gowers, The Importance of Mathematics, 2000
Valeria de Paiva and Samuel Gomes da Silva (EBL2014) March, 2014 3 / 31](https://image.slidesharecdn.com/dialcardinalities-march2014-140420163154-phpapp01/85/Dialectica-Categories-and-Cardinalities-of-the-Continuum-March2014-3-320.jpg)


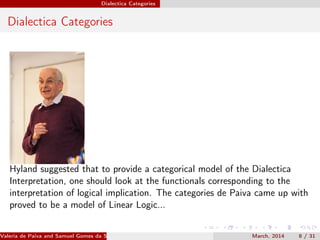
![Dialectica Categories
Gödel’s Incompleteness
Gödel’s incompleteness theorems (1931) showed that Hilbert’s program was
impossible to achieve, at least if interpreted in the most obvious way. BUT:
The development of proof theory itself is an outgrowth of
Hilbert’s program. Gentzen’s development of natural deduction
and the sequent calculus [too]. Gödel obtained his incompleteness
theorems while trying to prove the consistency of analysis. The
tradition of reductive proof theory of the Gentzen-Schütte school
is itself a direct continuation of Hilbert’s program.
R. Zach 2005
Valeria de Paiva and Samuel Gomes da Silva (EBL2014) March, 2014 6 / 31](https://image.slidesharecdn.com/dialcardinalities-march2014-140420163154-phpapp01/85/Dialectica-Categories-and-Cardinalities-of-the-Continuum-March2014-6-320.jpg)













![Cardinal characteristics
The structure of PV
Proposition[Rangel] The object (R, R, =) is maximal amongst objects of
PV.
Given any object A = (U, X, α) of PV we know both U and X have
cardinality small than |R|. In particular this means that there is an injective
function ϕ: U → R. (let ψ be its left inverse, i.e ψ(ϕu) = u)
Since α is a relation α ⊆ U × X over non-empty sets, if one accepts the
Axiom of Choice, then for each such α there is a map f : U → X such
that for all u in U, uαf(u).
Need a map Φ: R → X such that
U α X
⇑ ∀u ∈ U, ∀r ∈ R (ϕu = r) → α(u, Φr)
R
ϕ
?
= R
6
Φ
Valeria de Paiva and Samuel Gomes da Silva (EBL2014) March, 2014 21 / 31](https://image.slidesharecdn.com/dialcardinalities-march2014-140420163154-phpapp01/85/Dialectica-Categories-and-Cardinalities-of-the-Continuum-March2014-21-320.jpg)

![Cardinal characteristics
The structure of PV
Proposition[Rangel] The object (R, R, =) is minimal amongst objects of
PV.
This time we use the cardinality function ϕ: X → R for X. We want a
map in PV of the shape:
R = R
⇑ ∀r ∈ R, ∀x ∈ X α(Φr, x) → (r = ϕx)
U
Φ
?
α X
6
ϕ
Now using Choice again, given the relation α ⊆ U × X we can fix a
function g: X → U such that for any x in X g(x) is such that ¬g(x)αx.
Valeria de Paiva and Samuel Gomes da Silva (EBL2014) March, 2014 23 / 31](https://image.slidesharecdn.com/dialcardinalities-march2014-140420163154-phpapp01/85/Dialectica-Categories-and-Cardinalities-of-the-Continuum-March2014-23-320.jpg)






