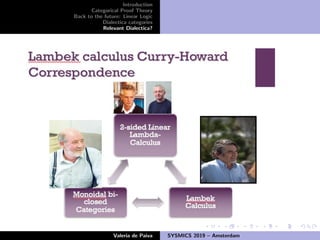
The document discusses the history and connections between logic, proofs, programs, and category theory. It notes that Hilbert's program to formalize mathematics led to the development of proof theory and Gentzen's natural deduction and sequent calculus systems. The Curry-Howard correspondence showed that proofs and programs are closely related through the use of lambda calculus. Category theory provides a unified framework where types represent logical formulas, terms represent proofs, and reductions represent proof normalization. Categorical proof theory models proofs as first-class citizens.











![Introduction
Categorical Proof Theory
Back to the future: Linear Logic
Dialectica categories
Relevant Dialectica?
G¨odel’s Incompleteness Theorems (1931)
Hilbert’s program impossible. BUT:
The development of proof theory itself is an outgrowth of
Hilbert’s program. Gentzen’s development of natural
deduction and the sequent calculus [too]. G¨odel obtained
his incompleteness theorems while trying to prove the
consistency of analysis. The tradition of reductive proof
theory of the Gentzen-Sch¨utte school is itself a direct
continuation of Hilbert’s program.
R. Zach, 2005
Valeria de Paiva SYSMICS 2019 – Amsterdam](https://image.slidesharecdn.com/sysmics2019-190303152859/85/A-Dialectica-Model-of-Relevant-Type-Theory-13-320.jpg)



![Introduction
Categorical Proof Theory
Back to the future: Linear Logic
Dialectica categories
Relevant Dialectica?
Curry-Howard for Implication
Natural deduction rules for implication (without λ-terms)
A → B A
B
[A]
·
·
·
·
π
B
A → B
Natural deduction rules for implication (with λ-terms)
M : A → B N : A
M(N): B
[x : A]
·
·
·
·
π
M : B
λx.M : A → B
function application abstraction
Valeria de Paiva SYSMICS 2019 – Amsterdam](https://image.slidesharecdn.com/sysmics2019-190303152859/85/A-Dialectica-Model-of-Relevant-Type-Theory-17-320.jpg)




















![Introduction
Categorical Proof Theory
Back to the future: Linear Logic
Dialectica categories
Relevant Dialectica?
The Right Structure!
Do the “reverse engineering” necessary to obtain a model of Linear
Logic...
A ⊗ B → C if and only if A → [B −◦ C]
U × V (α ⊗ β)XV
× Y U
U α X
⇓ ⇓
W
f
?
γ Z
6
(g1, g2)
W V
× Y Z
?
(β −◦ γ)V × Z
6
Valeria de Paiva SYSMICS 2019 – Amsterdam](https://image.slidesharecdn.com/sysmics2019-190303152859/85/A-Dialectica-Model-of-Relevant-Type-Theory-38-320.jpg)