This presentation explains the Knuth-Morris-Pratt (KMP) algorithm used for efficient pattern searching in strings. It covers the concept of prefix functions, failure arrays, and step-by-step execution of the algorithm with examples. Ideal for computer science students and learners preparing for algorithm-related topics.

























![The Knuth-Morris-Pratt (KMP) algorithm
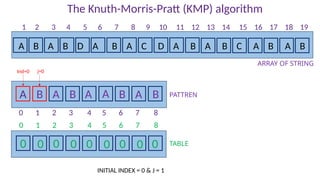
A B A B D A B A C D A B A B C A B A B
PATTREN
A B A B A A B A B
ARRAY OF STRING
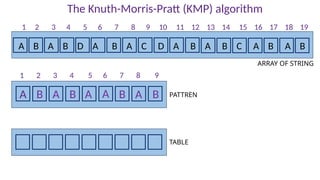
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0 1 2 3 4 5 6 7 8
TABLE
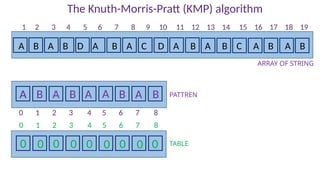
0 1 2 3 4 5 6 7 8
0 0 1 0 0 0 0 0 0
A == A Set table[2] = 1
Set ind = 1 and j =3
Ind=0 j=2](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-36-320.jpg)
![The Knuth-Morris-Pratt (KMP) algorithm
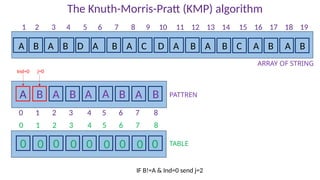
A B A B D A B A C D A B A B C A B A B
PATTREN
A B A B A A B A B
ARRAY OF STRING
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0 1 2 3 4 5 6 7 8
TABLE
0 1 2 3 4 5 6 7 8
0 0 1 2 0 0 0 0 0
B == B Set Table[3] = 2
Set Ind = 2 and j = 4
Ind=1 j=3](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-37-320.jpg)
![The Knuth-Morris-Pratt (KMP) algorithm
A B A B D A B A C D A B A B C A B A B
PATTREN
A B A B A A B A B
ARRAY OF STRING
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0 1 2 3 4 5 6 7 8
TABLE
0 1 2 3 4 5 6 7 8
0 0 1 2 3 0 0 0 0
A == A Set Table[4] = 3
Set Ind = 3 and j = 5
Ind=2 j=4](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-38-320.jpg)
![The Knuth-Morris-Pratt (KMP) algorithm
A B A B D A B A C D A B A B C A B A B
PATTREN
A B A B A A B A B
ARRAY OF STRING
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0 1 2 3 4 5 6 7 8
TABLE
0 1 2 3 4 5 6 7 8
0 0 1 2 3 0 0 0 0
A != B Set Ind > 0
Set Ind = Table[2] = 1
Ind=3 j=5](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-39-320.jpg)
![The Knuth-Morris-Pratt (KMP) algorithm
A B A B D A B A C D A B A B C A B A B
PATTREN
A B A B A A B A B
ARRAY OF STRING
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0 1 2 3 4 5 6 7 8
TABLE
0 1 2 3 4 5 6 7 8
0 0 1 2 3 0 0 0 0
A != B Set Ind > 0
Set Ind = Table[1] = 0
Ind=1 j=5](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-40-320.jpg)
![The Knuth-Morris-Pratt (KMP) algorithm
A B A B D A B A C D A B A B C A B A B
PATTREN
A B A B A A B A B
ARRAY OF STRING
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0 1 2 3 4 5 6 7 8
TABLE
0 1 2 3 4 5 6 7 8
0 0 1 2 3 4 0 0 0
A== A Set Table[5] = 1
Set Ins = 1 and j = 6
Ind=1 j=5](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-41-320.jpg)
![The Knuth-Morris-Pratt (KMP) algorithm
A B A B D A B A C D A B A B C A B A B
PATTREN
A B A B A A B A B
ARRAY OF STRING
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0 1 2 3 4 5 6 7 8
TABLE
0 1 2 3 4 5 6 7 8
0 0 1 2 3 4 5 0 0
B== B Set Table[6] = 2
Set Ins = 2 and j = 7
Ind=2 j=6](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-42-320.jpg)
![The Knuth-Morris-Pratt (KMP) algorithm
A B A B D A B A C D A B A B C A B A B
PATTREN
A B A B A A B A B
ARRAY OF STRING
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0 1 2 3 4 5 6 7 8
TABLE
0 1 2 3 4 5 6 7 8
0 0 1 2 3 1 2 3 0
A== A Set Table[7] = 3
Set Ins = 3 and j = 8
Ind=2 j=7](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-43-320.jpg)
![The Knuth-Morris-Pratt (KMP) algorithm
A B A B D A B A C D A B A B C A B A B
PATTREN
A B A B A A B A C
ARRAY OF STRING
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0 1 2 3 4 5 6 7 8
TABLE
0 1 2 3 4 5 6 7 8
0 0 1 2 3 1 2 3 0
C == B Set Table[8] = 0
Set Ins = 3 and j = 8
Ind=3 j=8](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-44-320.jpg)
![The Knuth-Morris-Pratt (KMP) algorithm
A B A B D A B A C D A B A B C A B A B
PATTREN
A B A B A A B A C
ARRAY OF STRING
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0 1 2 3 4 5 6 7 8
TABLE
0 1 2 3 4 5 6 7 8
0 0 1 2 3 1 2 3 0
C == B Set Table[8] = 0
Set Ins = 3 and j = 8
Ind=3 j=8](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-45-320.jpg)
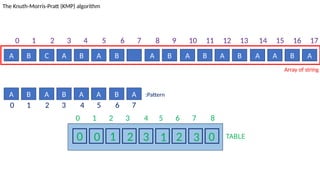
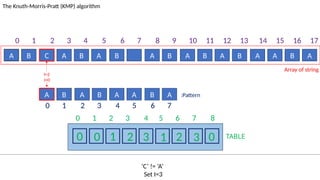
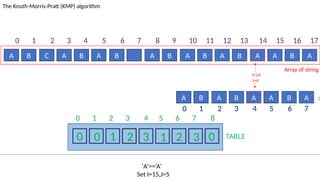
![TABLE
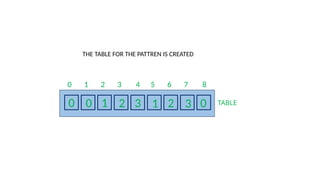
0 1 2 3 4 5 6 7 8
0 0 1 2 3 1 2 3 0
A B C A B A B A B A B A B A A B A
The Knuth-Morris-Pratt (KMP) algorithm
Array of string
A B A B A A B A :Pattern
‘C’ != ‘A’ and J!=0
Set J=T[J-1]=0
I=2
J=2
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
0 1 2 3 4 5 6 7](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-52-320.jpg)
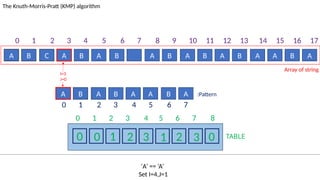
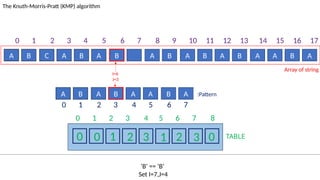
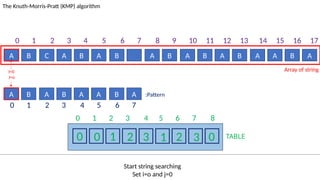
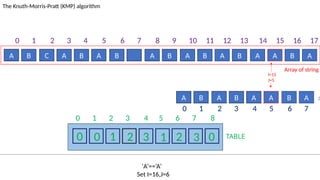
![TABLE
0 1 2 3 4 5 6 7 8
0 0 1 2 3 1 2 3 0
A B C A B A B A B A B A B A A B A
The Knuth-Morris-Pratt (KMP) algorithm
Array of string
A B A B A A B A :Pattern
‘ ’! = ‘A’ and J!=0.
Set J=T[J-1]=2
I=7
J=4
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
0 1 2 3 4 5 6 7](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-58-320.jpg)
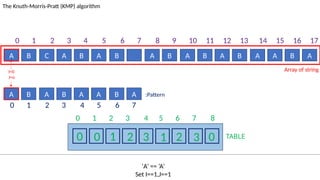
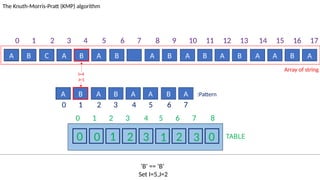
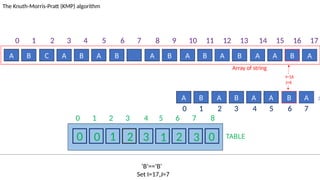
![TABLE
0 1 2 3 4 5 6 7 8
0 0 1 2 3 1 2 3 0
A B C A B A B A B A B A B A A B A
The Knuth-Morris-Pratt (KMP) algorithm
Array of string
A B A B A A B A :Pattern
‘ ’! = ‘A’ and J!=0.
Set J=T[J-1]=0
I=7
J=2
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
0 1 2 3 4 5 6 7](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-59-320.jpg)
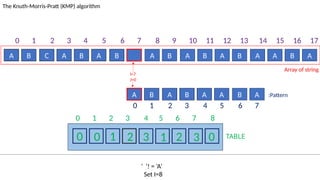
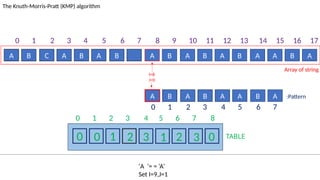
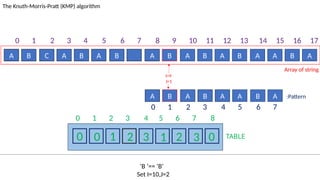
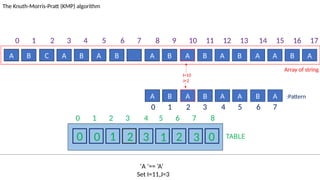
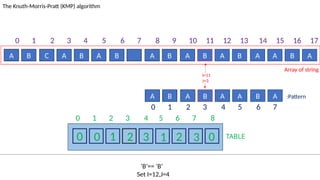
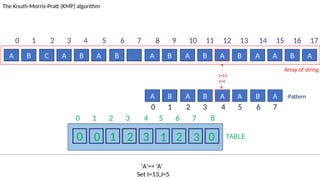
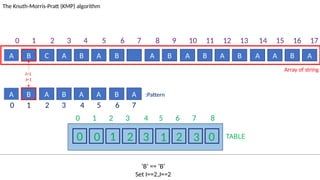
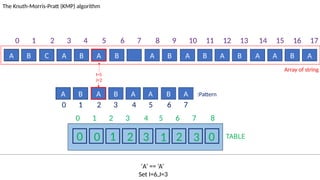
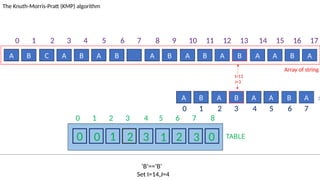
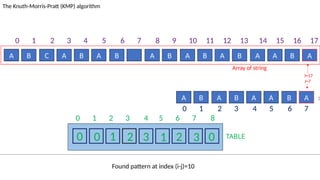
![TABLE
0 1 2 3 4 5 6 7 8
0 0 1 2 3 1 2 3 0
A B C A B A B A B A B A B A A B A
The Knuth-Morris-Pratt (KMP) algorithm
Array of string
A B A B A A B A :Pattern
‘B’!= ‘A’ and J!=0.
Set J=T[I-1]= 3
I=13
J=5
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
0 1 2 3 4 5 6 7](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-66-320.jpg)


![C code for the KMP algorithm:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void computeLPS(char *pattern, int M, int *lps) {
int len = 0;
lps[0] = 0;
int i = 1;
while (i < M) {
if (pattern[i] == pattern[len]) {
len++;
lps[i] = len;
i++;
} else {
if (len != 0) {
len = lps[len - 1];
} else {
lps[i] = 0;
i++;
}
}
}
void KMPSearch(char *text, char *pattern) {
int M = strlen(pattern);
int N = strlen(text);
int *lps = (int *)malloc(sizeof(int) * M);
if (lps == NULL) {
fprintf(stderr, "Memory allocation failed.n");
exit(EXIT_FAILURE);
}
computeLPS(pattern, M, lps);
int i = 0;
int j = 0;
while (i < N) {
if (pattern[j] == text[i]) {
j++;
i++;
}
if (j == M) {
printf("Pattern found at index %dn", i - j);
j = lps[j - 1];
} else if (i < N && pattern[j] != text[i]) {
if (j != 0) {
j = lps[j - 1];
} else {
i++;
}
}
}](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-75-320.jpg)
![}
free(lps);
}
int main() {
char text[] = "ABABDABACDABABCABAB";
char pattern[] = "ABABCABAB";
printf("Text: %sn", text);
printf("Pattern: %sn", pattern);
KMPSearch(text, pattern);
return 0;
}
C code for the KMP algorithm:](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-76-320.jpg)
![#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void computeLPS(char *pattern,
int M, int *lps) {
int len = 0;
lps[0] = 0;
int i = 1;
while (i < M) {
if (pattern[i] == pattern[len]) {
len++;
lps[i] = len;
i++;
} else {
if (len != 0) {
len = lps[len - 1];
} else {
lps[i] = 0;
i++;
}
}
}
}](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-77-320.jpg)

![#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void computeLPS(char *pattern,
int M, int *lps) {
int len = 0;
lps[0] = 0;
int i = 1;
while (i < M) {
if (pattern[i] == pattern[len]) {
len++;
lps[i] = len;
i++;
} else {
if (len != 0) {
len = lps[len - 1];
} else {
lps[i] = 0;
i++;
}
}
}
}](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-79-320.jpg)
![void computeLPS(char *pattern,
int M, int *lps) {
int len = 0;
lps[0] = 0;
int i = 1;
This line defines a function named computeLPS that computes the Longest
Prefix which is also a Suffix (LPS) array for a given pattern. It takes three
parameters: pattern (the pattern string), M (length of the pattern), and lps (an
array to store the computed LPS values).](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-80-320.jpg)
![#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void computeLPS(char *pattern, int M,
int *lps) {
int len = 0;
lps[0] = 0;
int i = 1;
while (i < M) {
if (pattern[i] == pattern[len]) {
len++;
lps[i] = len;
i++;
} else {
if (len != 0) {
len = lps[len - 1];
} else {
lps[i] = 0;
i++;
}
}
}
}](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-81-320.jpg)
![while (i < M) {
if (pattern[i] == pattern[len]) {
len++;
lps[i] = len;
i++;
} else {
if (len != 0) {
len = lps[len - 1];
} else {
lps[i] = 0;
i++;
}
}
}
}
This initializes a variable i to 1 and starts a while loop that iterates through the
pattern and checks if the current characters in the pattern at positions i and len are
equal. If they are, it increments len, sets lps[i] to the current value of len, and
increments i. If the characters are not equal, it goes to the else part.](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-82-320.jpg)
![while (i < N) {
if (pattern[j] == text[i]) {
j++;
i++;
}
if (j == M) {
printf("Pattern found at index %dn", i - j);
j = lps[j - 1];
} else if (i < N && pattern[j] != text[i]) {
if (j != 0) {
j = lps[j - 1];
} else {
i++;
}
}
}
free(lps);
}
void KMPSearch(char *text, char *pattern) {
int M = strlen(pattern);
int N = strlen(text);
int *lps = (int *)malloc(sizeof(int) * M);
if (lps == NULL) {
fprintf(stderr, "Memory allocation failed.n");
exit(EXIT_FAILURE);
}
computeLPS(pattern, M, lps);
int i = 0;
int j = 0;](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-83-320.jpg)

![while (i < N) {
if (pattern[j] == text[i]) {
j++;
i++;
}
if (j == M) {
printf("Pattern found at index %dn", i - j);
j = lps[j - 1];
} else if (i < N && pattern[j] != text[i]) {
if (j != 0) {
j = lps[j - 1];
} else {
i++;
}
}
}
free(lps);
}
void KMPSearch(char *text, char *pattern) {
int M = strlen(pattern);
int N = strlen(text);
int *lps = (int *)malloc(sizeof(int) * M);
if (lps == NULL) {
fprintf(stderr, "Memory allocation failed.n");
exit(EXIT_FAILURE);
}
computeLPS(pattern, M, lps);
int i = 0;
int j = 0;](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-85-320.jpg)

![while (i < N) {
if (pattern[j] == text[i]) {
j++;
i++;
}
if (j == M) {
printf("Pattern found at index %dn", i - j);
j = lps[j - 1];
} else if (i < N && pattern[j] != text[i]) {
if (j != 0) {
j = lps[j - 1];
} else {
i++;
}
}
}
free(lps);
}
void KMPSearch(char *text, char *pattern) {
int M = strlen(pattern);
int N = strlen(text);
int *lps = (int *)malloc(sizeof(int) * M);
if (lps == NULL) {
fprintf(stderr, "Memory allocation failed.n");
exit(EXIT_FAILURE);
}
computeLPS(pattern, M, lps);
int i = 0;
int j = 0;](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-87-320.jpg)

![while (i < N) {
if (pattern[j] == text[i]) {
j++;
i++;
}
if (j == M) {
printf("Pattern found at index %dn", i - j);
j = lps[j - 1];
} else if (i < N && pattern[j] != text[i]) {
if (j != 0) {
j = lps[j - 1];
} else {
i++;
}
}
}
free(lps);
}
void KMPSearch(char *text, char *pattern) {
int M = strlen(pattern);
int N = strlen(text);
int *lps = (int *)malloc(sizeof(int) * M);
if (lps == NULL) {
fprintf(stderr, "Memory allocation failed.n");
exit(EXIT_FAILURE);
}
computeLPS(pattern, M, lps);
int i = 0;
int j = 0;](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-89-320.jpg)
![while (i < N) {
if (pattern[j] == text[i]) {
j++;
i++;
}
if (j == M) {
printf("Pattern found at index %dn", i -
j);
j = lps[j - 1];
} else if (i < N && pattern[j] != text[i]) {
if (j != 0) {
j = lps[j - 1];
} else {
i++;
}
}
}
free(lps);
}
while (i < N) {: Loop through the text.
if (pattern[j] == text[i]) { j++; i++; }: Match characters,
advancing indices.
if (j == M) { printf("Pattern found at index %dn", i -
j); j = lps[j - 1]; }: Check if pattern is found, print, and
adjust pattern index.
else if (i < N && pattern[j] != text[i]) { j = (j != 0) ? lps[j
- 1] : 0; i += (j == 0); }: Handle non-matching
characters, adjust indices based on LPS array.](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-90-320.jpg)
![int main() {
char text[] = "ABABDABACDABABCABAB";
char pattern[] = "WrongPattern"; // Change to a pattern that is not in the text
printf("Text: %sn", text);
printf("Pattern: %sn", pattern);
KMPSearch(text, pattern);
return 0;
}](https://image.slidesharecdn.com/kmp-251022070411-dd00bf52/85/Detailed-Presentation-on-KMP-Algorithm-for-Efficient-Pattern-Searching-91-320.jpg)
