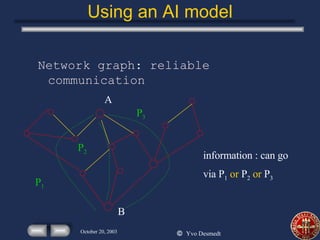
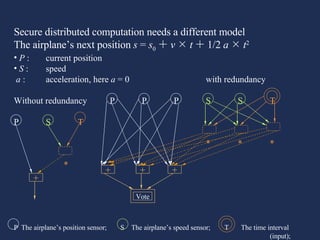
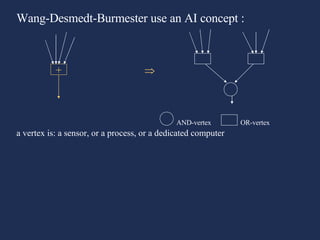
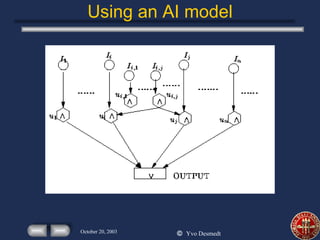
This presentation discusses using economics and AI to identify critical infrastructures. It summarizes issues with traditional models and proposes using AND/OR graphs and flow models to better integrate computer and mechanical systems. The presentation also discusses modeling an adversary's objectives and budget to optimize attacks, and using costs and capacities to model competitive strategies between defenders and attackers.