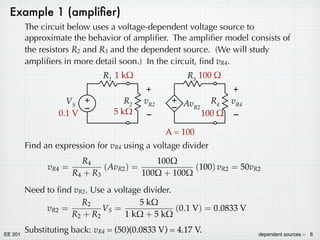
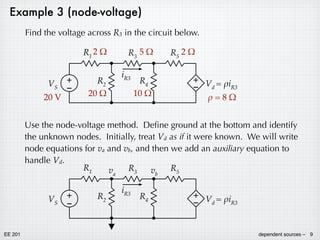
Dependent sources behave like independent voltage and current sources, except that their voltage or current depends on another voltage or current in the circuit. There are four types of dependent sources: voltage-controlled voltage source, current-controlled voltage source, voltage-controlled current source, and current-controlled current source. Circuit analysis proceeds similarly to circuits with independent sources, though source transformations must be used carefully with dependent sources.