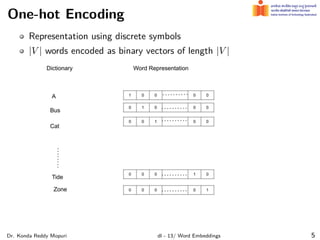
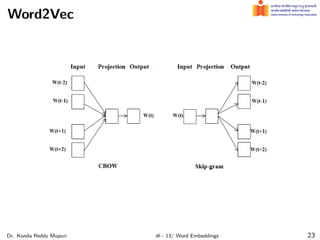
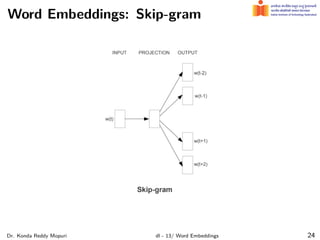
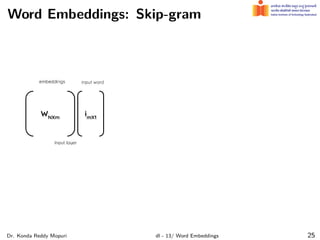
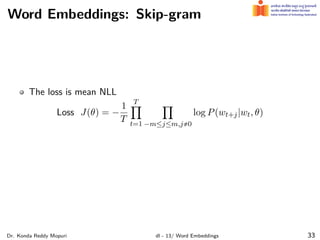
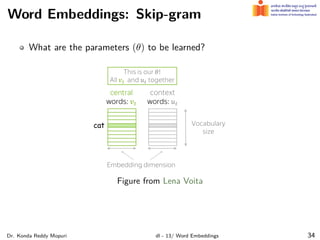
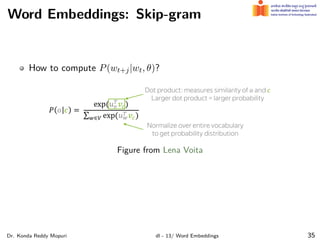
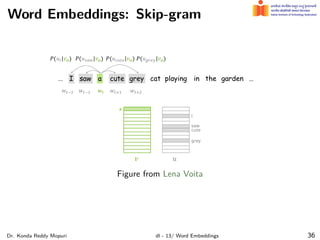
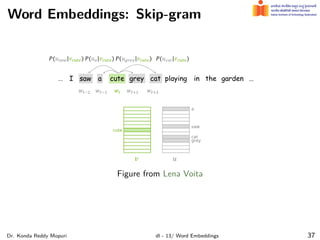
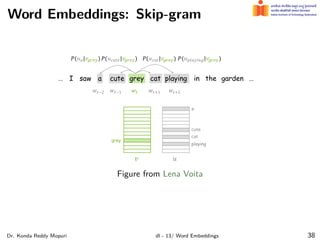
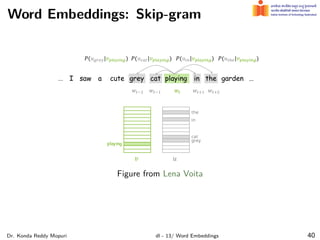
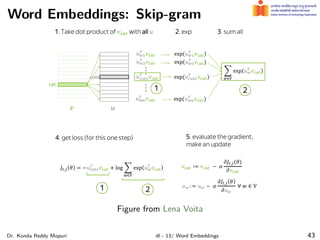
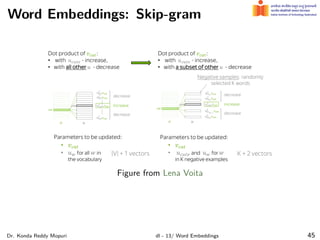
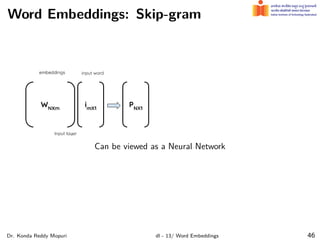
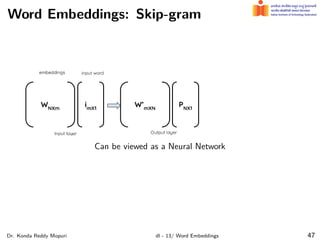
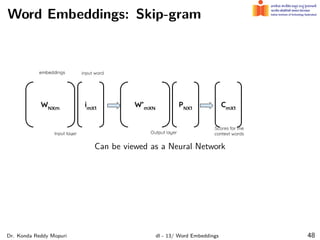
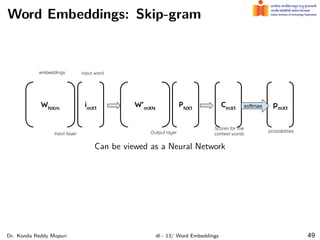
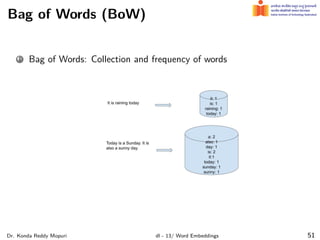
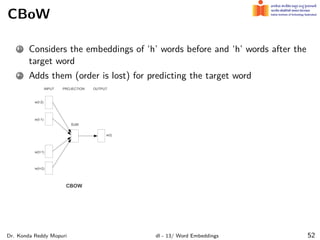
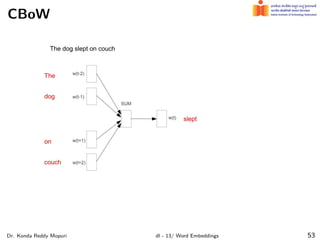
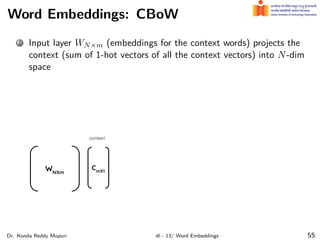
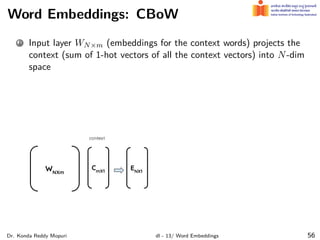
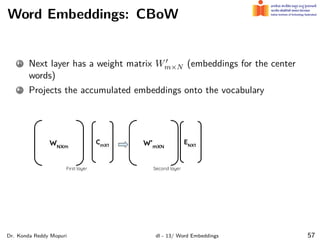
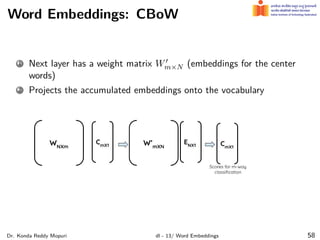
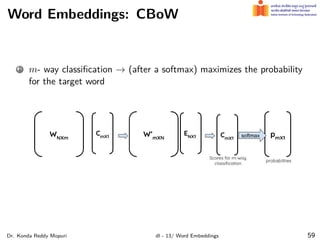
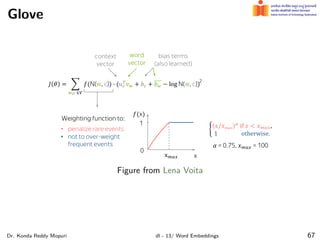
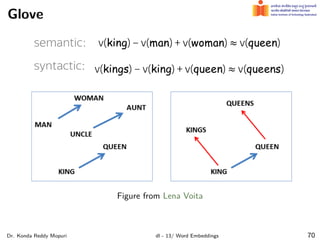
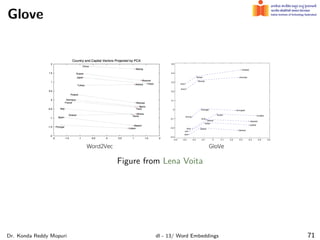
The document discusses word embeddings and their significance in deep learning, highlighting the limitations of one-hot encoding in representing word semantics. It describes the distributional hypothesis and introduces techniques such as co-occurrence matrices and dimensionality reduction using SVD. Furthermore, it covers prediction-based models like Word2Vec, including CBOW and skip-gram models, and their training processes to capture word meanings based on context.

1. Deep Learning
13 Word Embeddings
Dr. Konda Reddy Mopuri
Dept. of AI, IIT Hyderabad
Jan-May 2024
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 1

2. Why Word Embeddings?
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 2

3. Why Word Embeddings?
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 3

4. Terminology
Corpus: a collection of authentic text organized into dataset
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 4

5. Terminology
Corpus: a collection of authentic text organized into dataset
Vocabulary (V): Set of allowed words
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 4

6. Terminology
Corpus: a collection of authentic text organized into dataset
Vocabulary (V): Set of allowed words
Target: Representation for every word in V
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 4

7. One-hot Encoding
Representation using discrete symbols
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 5

8. One-hot Encoding
Representation using discrete symbols
|V | words encoded as binary vectors of length |V |
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 5

9. One-hot encoding: Drawbacks
1 Space inefficient (e.g. 13M words in Google 1T corpus)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 6

10. One-hot encoding: Drawbacks
1 Space inefficient (e.g. 13M words in Google 1T corpus)
2 No notion of similarity (or, distance) between words
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 6

11. One-hot encoding: Drawbacks
1 Space inefficient (e.g. 13M words in Google 1T corpus)
2 No notion of similarity (or, distance) between words
‘Dog’ is as close to ‘Cat’ as it is to ‘Machine’
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 6

12. Notion of Meaning for words
1 What is a good notion of meaning for a word?
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 7

13. Notion of Meaning for words
1 What is a good notion of meaning for a word?
2 How do we, humans, know the meaning of a word?
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 7

14. Notion of Meaning for words
1 What does silla mean?
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 8

15. Notion of Meaning for words
1 Let’s see how this word is used in different contexts
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 9

16. Notion of Meaning for words
1 Does this context help you understand the word silla?
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 10

17. Notion of Meaning for words
1 Does this context help you understand the word silla?
2 { positioned near a window or against a wall or in the corner, used for
conversing/events, can be used to relax }
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 10

18. Notion of Meaning for words
1 How did we do that?
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 11

19. Notion of Meaning for words
1 How did we do that?
2 “We searched for other words that can be used in the same contexts,
found some, and made a conclusion that silla has to mean similar to
those words."
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 11

20. Notion of Meaning for words
1 Distributional Hypothesis: Words that frequently appear in similar
contexts have a similar meaning
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 12

21. Distributed Representations
1 Representation/meaning of a word should consider its context in the
corpus
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 13

22. Distributed Representations
1 Representation/meaning of a word should consider its context in the
corpus
2 Use many contexts of a word to build up a representation for it
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 13

23. Distributed Representations
1 Co-occurrence matrix is a way to can capture this!
size: (#words × #words)
rows: words (m), cols: context (n)
words and context can be of same or different size
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 14

24. Distributed Representations
1 Co-occurrence matrix is a way to can capture this!
size: (#words × #words)
rows: words (m), cols: context (n)
words and context can be of same or different size
2 Context can be defined as a ‘h’ word neighborhood
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 14

25. Distributed Representations
1 Co-occurrence matrix is a way to can capture this!
size: (#words × #words)
rows: words (m), cols: context (n)
words and context can be of same or different size
2 Context can be defined as a ‘h’ word neighborhood
3 Each row (column): vectorial representation of the word (context)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 14

26. Co-occurrence matrix
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 15

27. Co-occurrence matrix
1 Very sparse
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 16

28. Co-occurrence matrix
1 Very sparse
2 Very high-dimensional (grows with the vocabulary size)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 16

29. Co-occurrence matrix
1 Very sparse
2 Very high-dimensional (grows with the vocabulary size)
3 Solution:Dimensionality reduction (SVD)!
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 16

30. SVD on the Co-occurrence matrix
1 X = UΣV T
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 17

31. SVD on the Co-occurrence matrix
1 X = UΣV T
2

 X


m×n
=


↑ . . . ↑
u1 . . . uk
↓ . . . ↓


m×k
·



σ1
...
σk



k×k
·



← vT
1 →
.
.
.
← vT
k →



k×n
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 17

32. SVD on the Co-occurrence matrix
1 X = UΣV T
2

 X


m×n
=


↑ . . . ↑
u1 . . . uk
↓ . . . ↓


m×k
·



σ1
...
σk



k×k
·



← vT
1 →
.
.
.
← vT
k →



k×n
3 X = σ1u1vT
1 + σ2u2vT
2 + . . . + σkukvT
k
4 X̂ =
∑d<k
i=1 σiuivT
i is a d-rank approximation of X
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 17

33. SVD on the Co-occurrence matrix
1 Before the SVD, representations were the rows of X
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 18

34. SVD on the Co-occurrence matrix
1 Before the SVD, representations were the rows of X
2 How do we reduce the representation size with SVD ?
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 18

35. SVD on the Co-occurrence matrix
1 Before the SVD, representations were the rows of X
2 How do we reduce the representation size with SVD ?
3 Wword = Um×k · Σk×k
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 18

36. SVD on the Co-occurrence matrix
1 Wword ∈ Rm×k (k ≪ |V | = m) are considered the representation of
the words
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 19

37. SVD on the Co-occurrence matrix
1 Wword ∈ Rm×k (k ≪ |V | = m) are considered the representation of
the words
2 Lesser dimensions but the same similarities! (one may verify that
XXT = X̂X̂T )
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 19

38. SVD on the Co-occurrence matrix
1 Wword ∈ Rm×k (k ≪ |V | = m) are considered the representation of
the words
2 Lesser dimensions but the same similarities! (one may verify that
XXT = X̂X̂T )
3 Wcontext = V ∈ Rn×k are taken as the representations for the context
words
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 19

39. A bit more clever things...
1 Entries in the occurrence matrix can be weighted (HAL model)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 20

40. A bit more clever things...
1 Entries in the occurrence matrix can be weighted (HAL model)
2 Better associations can be used (PPMI)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 20

41. A bit more clever things...
1 Entries in the occurrence matrix can be weighted (HAL model)
2 Better associations can be used (PPMI)
3 ....
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 20

42. Count-based vs prediction-based models
1 Techniques we have seen so far rely on the counts (or, co-occurrence
of words)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 21

43. Count-based vs prediction-based models
1 Techniques we have seen so far rely on the counts (or, co-occurrence
of words)
2 Next, we see prediction based models for word embeddings
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 21

44. Word2Vec
1 T Mikolov et al. (2013)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 22

45. Word2Vec
1 T Mikolov et al. (2013)
2 Two versions: Predict words from the contexts (or contexts from
words)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 22

46. Word2Vec
1 T Mikolov et al. (2013)
2 Two versions: Predict words from the contexts (or contexts from
words)
3 Continuous Bag of Words (CBoW) and Skip-gram
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 22

47. Word2Vec
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 23

48. Word Embeddings: Skip-gram
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 24

49. Word Embeddings: Skip-gram
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 25

50. Word Embeddings: Skip-gram
1 Start: huge corpus and random initialization of the word embeddings
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 26

51. Word Embeddings: Skip-gram
1 Start: huge corpus and random initialization of the word embeddings
2 Process the text with a sliding window (one word at a time)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 26

52. Word Embeddings: Skip-gram
1 Start: huge corpus and random initialization of the word embeddings
2 Process the text with a sliding window (one word at a time)
1 At each step, there is a central word and context words (other words
in the window)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 26

53. Word Embeddings: Skip-gram
1 Start: huge corpus and random initialization of the word embeddings
2 Process the text with a sliding window (one word at a time)
1 At each step, there is a central word and context words (other words
in the window)
2 Given the central word, compute the probabilities for the context
words
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 26

54. Word Embeddings: Skip-gram
1 Start: huge corpus and random initialization of the word embeddings
2 Process the text with a sliding window (one word at a time)
1 At each step, there is a central word and context words (other words
in the window)
2 Given the central word, compute the probabilities for the context
words
3 Modify the word embeddings to increase these probabilities
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 26

55. Word Embeddings: Skip-gram
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 27

56. Word Embeddings: Skip-gram
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 28

57. Word Embeddings: Skip-gram
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 29

58. Word Embeddings: Skip-gram
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 30

59. Word Embeddings: Skip-gram
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 31

60. Word Embeddings: Skip-gram
For each position in t = 1, 2, . . . T in the corpus, Skip-gram predicts
the context words in m−sized window (θ is the variables to be
optimized)
Likelihood L(θ) =
T
∏
t=1
∏
−m≤j≤m,j,0
P(wt+j|wt, θ)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 32

61. Word Embeddings: Skip-gram
The loss is mean NLL
Loss J(θ) = −
1
T
T
∏
t=1
∏
−m≤j≤m,j,0
log P(wt+j|wt, θ)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 33

62. Word Embeddings: Skip-gram
What are the parameters (θ) to be learned?
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 34

63. Word Embeddings: Skip-gram
How to compute P(wt+j|wt, θ)?
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 35

64. Word Embeddings: Skip-gram
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 36

65. Word Embeddings: Skip-gram
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 37

66. Word Embeddings: Skip-gram
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 38

67. Word Embeddings: Skip-gram
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 39

68. Word Embeddings: Skip-gram
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 40

69. Word Embeddings: Skip-gram
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 41

70. Word Embeddings: Skip-gram
Train using Gradient Descent
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 42

71. Word Embeddings: Skip-gram
Train using Gradient Descent
For one word at a time, i.e., (a center word, one of the context words)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 42

72. Word Embeddings: Skip-gram
Train using Gradient Descent
For one word at a time, i.e., (a center word, one of the context words)
Jt,j(θ) = − log P(cute|cat) = − log
exp uT
cutevcat
∑
w∈V oc
exp uT
wvcat
=
−uT
cutevcat + log
∑
w∈V oc
exp uT
wvcat
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 42

73. Word Embeddings: Skip-gram
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 43

74. Word Embeddings: Skip-gram
Training is slow (for each central word, all the context words need to
be updated)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 44

75. Word Embeddings: Skip-gram
Training is slow (for each central word, all the context words need to
be updated)
Negative sampling: not all the context words are considered, but a
random sample of them
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 44

76. Word Embeddings: Skip-gram
Training is slow (for each central word, all the context words need to
be updated)
Negative sampling: not all the context words are considered, but a
random sample of them
Training over a large corpus leads to sufficient updates for each vector
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 44

77. Word Embeddings: Skip-gram
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 45

78. Word Embeddings: Skip-gram
Can be viewed as a Neural Network
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 46

79. Word Embeddings: Skip-gram
Can be viewed as a Neural Network
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 47

80. Word Embeddings: Skip-gram
Can be viewed as a Neural Network
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 48

81. Word Embeddings: Skip-gram
Can be viewed as a Neural Network
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 49

82. Word Embeddings: Skip-gram
1 WN×m is the Wword (used for representing the words)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 50

83. Word Embeddings: Skip-gram
1 WN×m is the Wword (used for representing the words)
2 W′
m×N is the Wcontext (may be ignored after the training)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 50

84. Word Embeddings: Skip-gram
1 WN×m is the Wword (used for representing the words)
2 W′
m×N is the Wcontext (may be ignored after the training)
3 Some showed averaging word and context vectors may be more
beneficial
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 50

85. Bag of Words (BoW)
1 Bag of Words: Collection and frequency of words
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 51

86. CBoW
1 Considers the embeddings of ‘h’ words before and ‘h’ words after the
target word
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 52

87. CBoW
1 Considers the embeddings of ‘h’ words before and ‘h’ words after the
target word
2 Adds them (order is lost) for predicting the target word
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 52

88. CBoW
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 53

89. CBoW
1 Size of the vocabulary = m
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 54

90. CBoW
1 Size of the vocabulary = m
2 Dimension of the embeddings = N
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 54

91. Word Embeddings: CBoW
1 Input layer WN×m (embeddings for the context words) projects the
context (sum of 1-hot vectors of all the context vectors) into N-dim
space
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 55

92. Word Embeddings: CBoW
1 Input layer WN×m (embeddings for the context words) projects the
context (sum of 1-hot vectors of all the context vectors) into N-dim
space
2 Representations of all the (2h) words in the context are summed
(result is an N-dim context vector)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 55

93. Word Embeddings: CBoW
1 Input layer WN×m (embeddings for the context words) projects the
context (sum of 1-hot vectors of all the context vectors) into N-dim
space
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 56

94. Word Embeddings: CBoW
1 Input layer WN×m (embeddings for the context words) projects the
context (sum of 1-hot vectors of all the context vectors) into N-dim
space
2 Representations of all the (2h) words in the context are summed
(result is an N-dim context vector)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 56

95. Word Embeddings: CBoW
1 Next layer has a weight matrix W′
m×N (embeddings for the center
words)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 57

96. Word Embeddings: CBoW
1 Next layer has a weight matrix W′
m×N (embeddings for the center
words)
2 Projects the accumulated embeddings onto the vocabulary
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 57

97. Word Embeddings: CBoW
1 Next layer has a weight matrix W′
m×N (embeddings for the center
words)
2 Projects the accumulated embeddings onto the vocabulary
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 58

98. Word Embeddings: CBoW
1 m- way classification → (after a softmax) maximizes the probability
for the target word
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 59

99. Word Embeddings: CBoW
1 WN×m is the Wcontext
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 60

100. Word Embeddings: CBoW
1 WN×m is the Wcontext
2 W′
m×N is the Wwords
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 60

101. Glove
1 Glove - Global Vectors
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 61

102. Glove
1 Glove - Global Vectors
2 Combines the score-based and predict-based approaches
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 61

103. Glove
1 Xij in the co-occurrence matrix encodes the global info. about words
i and j
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 62

104. Glove
1 Xij in the co-occurrence matrix encodes the global info. about words
i and j
p(j/i) =
Xij
Xi
2 Glove attempts to learn representations that are faithful to the
co-occurrence info.
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 62

105. Glove
1 Glove attempts to learn representations that are faithful to the
co-occurrence info.
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 63

106. Glove
1 Glove attempts to learn representations that are faithful to the
co-occurrence info.
2 Try to enforce vT
i cj = log P(j/i) = log Xij − log Xi
vi - central representation of word i, cj - context representation of
word j
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 63

107. Glove
1 Glove attempts to learn representations that are faithful to the
co-occurrence info.
2 Try to enforce vT
i cj = log P(j/i) = log Xij − log Xi
vi - central representation of word i, cj - context representation of
word j
3 Similarly, vT
j ci = log P(i/j) = log Xij − log Xj (aim is to learn such
embeddings vi and ci)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 63

108. Glove
1 To realize the exchange symmetry of
vT
i cj = log P(j/i) = log Xij − log Xi
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 64

109. Glove
1 To realize the exchange symmetry of
vT
i cj = log P(j/i) = log Xij − log Xi
we may capture the log Xi as a bias bi of the word wi
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 64

110. Glove
1 To realize the exchange symmetry of
vT
i cj = log P(j/i) = log Xij − log Xi
we may capture the log Xi as a bias bi of the word wi
And, an additional term ˜
bj
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 64

111. Glove
1 To realize the exchange symmetry of
vT
i cj = log P(j/i) = log Xij − log Xi
we may capture the log Xi as a bias bi of the word wi
And, an additional term ˜
bj
2 vT
i cj + bi + ˜
bj = log Xij
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 64

112. Glove
1 To realize the exchange symmetry of
vT
i cj = log P(j/i) = log Xij − log Xi
we may capture the log Xi as a bias bi of the word wi
And, an additional term ˜
bj
2 vT
i cj + bi + ˜
bj = log Xij
3 Since log Xi and log Xj depend on the words i and j, they can be
considered as the word specific biases (learnable)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 64

113. Glove
1 Learning objective becomes
argmin
vi,cj,bi, ˜
bj
J() =
∑
i,j
(
vT
i cj + bi + ˜
bj − log Xij
)2
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 65

114. Glove
1 Learning objective becomes
argmin
vi,cj,bi, ˜
bj
J() =
∑
i,j
(
vT
i cj + bi + ˜
bj − log Xij
)2
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 66

115. Glove
1 Learning objective becomes
argmin
vi,cj,bi, ˜
bj
J() =
∑
i,j
(
vT
i cj + bi + ˜
bj − log Xij
)2
2 Much of the entries in the co-occurrence matrix are zeros (noisy or
less informative)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 66

116. Glove
1 Learning objective becomes
argmin
vi,cj,bi, ˜
bj
J() =
∑
i,j
(
vT
i cj + bi + ˜
bj − log Xij
)2
2 Much of the entries in the co-occurrence matrix are zeros (noisy or
less informative)
3 Suggests to apply a weight
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 66

117. Glove
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 67

118. Evaluating the embeddings
1 Intrinsic - studying the internal properties (how well they capture the
meaning: word similarity, analogy, etc.)
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 68

119. Evaluating the embeddings
1 Intrinsic - studying the internal properties (how well they capture the
meaning: word similarity, analogy, etc.)
2 Extrinsic - studying how they perform a task
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 68

120. Analysing the embeddings
1 Walking the semantic space
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 69

121. Analysing the embeddings
1 Walking the semantic space
2 Structure - (form clusters) nearest neighbors have a similar meaning,
Linear structure
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 69

122. Glove
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 70

123. Glove
Figure from Lena Voita
Dr. Konda Reddy Mopuri dl - 13/ Word Embeddings 71