This document summarizes research on coupled quantum systems and decoherence. It discusses decoherence occurring when a quantum system interacts with its environment, preventing quantum superposition states from interfering. Decoherence is important for the emergence of classical physics from quantum mechanics. The document also summarizes studies on coupled quantum dots, electron-phonon coupling in nanostructures, cooling of weakly coupled quantum systems, and protecting quantum gates from decoherence through dynamical decoupling techniques.









![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
violation that we have not been able to detect yet, but which could have played an important role
during the very early universe, when most matter and antimatter annihilated and a small fraction of
the matter survived.
Physicists are searching for these unknown CP violation effects. We never know what exactly this
quest will yield, but as has always been the case in the history of particle physics, we expect to learn
a great deal about nature in the process. ( For more details Please see Abner Soffer of Colorado
State University)
NOTATION :
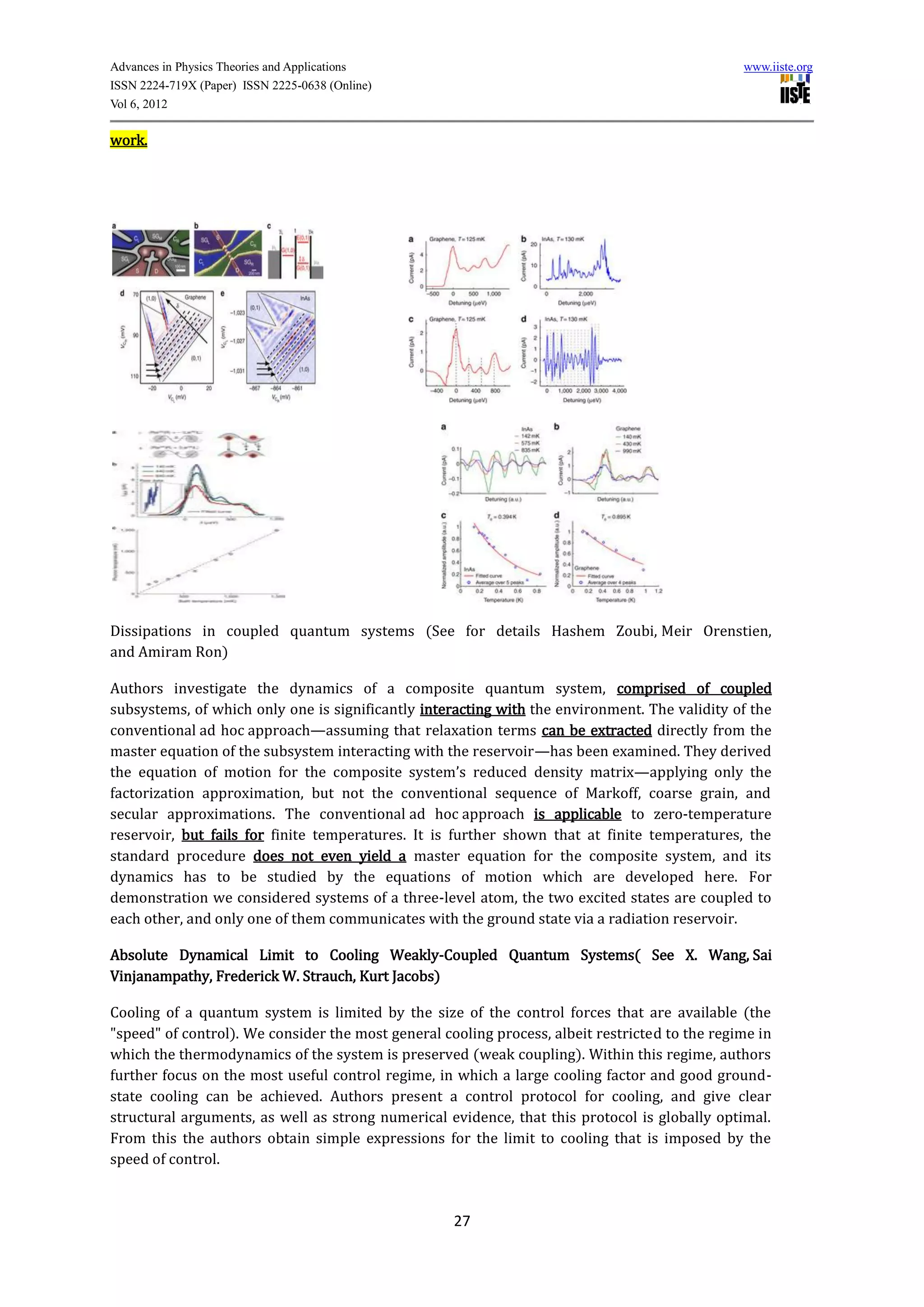
Coupled Quantum Systems And Decohering Environment:
: Category One Of Coupled Quantum System
: Category Two Of Coupled Quantum System
: Category Three Of Coupled Quantum System
: Category One Of Decohering Environment
: Category Two Of Decohering Environment
:Category Three Of Decohering Environment
Conflict Between Quantum Gate Operation And Decoupling And Internal Resonance In Coupled
Spin Systems: Module Numbered Two:
: Category One Of Conflict Between Quantum Gate Operation And Decoupling
: Category Two Of Conflict Between Quantum Gate Operation And Decoupling
: Category Three Conflict Between Quantum Gate Operation And Decoupling
: Category One Of Internal Resonance In Coupled Spin Systems
: Category Two Of Internal Resonance In Coupled Spin Systems
: Category Three Of Internal Resonance In Coupled Spin Systems
( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) ( )( ) , ( )( ) , ( )( )
( )( ) , ( )( ) , ( )( ) : are Accentuation coefficients
( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) ,
( )( ) , ( )( ) , ( )( )
are Dissipation coefficients
Governing Equations of The System Decohering Environment And Coupled Quantum Systems:
The differential system of this model is now
=( )( )
[( )( )
( )( ) ( , )] 1
=( )( )
[( )( )
( )( ) ( , )] 2
=( )( )
[( )( )
( )( ) ( , )] 3
=( )( )
[( )( )
( )( ) ( , )] 4
34](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-11-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
=( )( )
[( )( )
( )( ) ( , )] 5
=( )( )
[( )( )
( )( ) ( , )] 6
( )( ) ( , ) = First augmentation factor 7
( )( ) ( , ) = First detritions factor 8
Governing Equations of the System Conflict Between Quantum Gate Operations And Decoupling
And Internal Resonance In Coupled Spin Systems:
The differential system of this model is now
=( )( )
[( )( )
( )( ) ( , )] 9
=( )( )
[( )( )
( )( ) ( , )] 10
=( )( )
[( )( )
( )( ) ( , )] 11
=( )( )
[( )( )
( )( ) (( ), )] 12
=( )( )
[( )( )
( )( ) (( ), )] 13
=( )( )
[( )( )
( )( ) (( ), )] 14
( )( ) ( , ) = First augmentation factor 15
( )( ) (( ), ) = First detritions factor 16
Coupled Quantum Systems And Decohering Environment And The Conflict Between Quantum
Gate Operation And Decoupling And Internal Resonance In Coupled Spin Systems - The Final
Governing Equations
=( )( )
[( )( )
( )( ) ( , ) ( )( , )(
, ) ] 17
=( )( )
[( )( )
( )( ) ( , ) ( )( , )(
, ) ] 18
=( )( )
[( )( )
( )( ) ( , ) ( )( , )(
, ) ] 19
Where ( )( ) ( , ) , ( )( ) ( , ) ,( )( ) ( , ) are first augmentation coefficients for 20
category 1, 2 and 3
( )( , ) ( , ) , ( )( , )(
, ) , ( )( , )(
, ) are second augmentation coefficients 21
for category 1, 2 and 3
=( )( )
[( )( )
( )( ) ( , ) ( )( , )(
, ) ] 22
=( )( )
[( )( )
( )( ) ( , ) ( )( , )(
, ) ] 23
=( )( )
[( )( )
( )( ) ( , ) ( )( , )(
, ) ] 24
Where ( )( ) ( , ) , ( )( ) ( , ) , ( )( ) ( , ) are first detrition coefficients for category 25
1, 2 and 3
35](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-12-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
( )( , ) ( , ) , ( )( , )(
, ) , ( )( , )(
, ) are second augmentation coefficients for
category 1, 2 and 3
=( )( )
[( )( )
( )( ) ( , ) ( )( , )(
, ) ] 26
=( )( )
[( )( )
( )( ) ( , ) ( )( , )(
, ) ] 27
=( )( )
[( )( )
( )( ) ( , ) ( )( , )(
, ) ] 28
Where ( )( ) ( , ) , ( )( ) ( , ) , ( )( ) ( , ) are first augmentation coefficients 29
for category 1, 2 and 3
( )( , ) ( , ) , ( )( , )(
, ) , ( )( , )(
, ) are second detrition coefficients for
category 1, 2 and 3
=( )( )
[( )( )
( )( ) ( , ) ( )( , )(
, ) ] 30
=( )( )
[( )( )
( )( ) ( , ) ( )( , )(
, ) ] 31
=( )( )
[( )( )
( )( ) ( , ) ( )( , )(
, ) ] 32
Where ( )( ) ( , ) , ( )( ) ( , ) , ( )( ) ( , ) are first detrition coefficients for 33
category 1, 2 and 3
( )( , ) ( , ) , ( )( , ) ( , ) , ( )( , )(
, ) are second detrition coefficients for category
1, 2 and 3
Where we suppose
(A) ( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( )
0, 34
, = 1 ,14,15
(B) The functions ( )( ) , ( )( ) are positive continuous increasing and bounded.
Definition of ( )( ) , ( )( ) :
( )( ) ( , ) ( )( )
( ̂ )( )
( )( ) ( , ) ( )( )
( )( )
( ̂ )( )
(C) ( )( ) ( , ) = ( )( ) 35
lim ( )( ) ( , ) = ( )( )
Definition of ( ̂ )( ) , ( ̂ )( ) :
Where ( ̂ )( ) , ( ̂ )( ) , ( )( ) , ( )( )
are positive constants
and = 1 ,14,15
They satisfy Lipschitz condition: 36
)( )
|( )( ) ( , ) ( )( ) ( , )| (̂ )( ) | | ( ̂
)( )
|( )( ) ( , ) ( )( ) ( , )| (̂ )( ) || || ( ̂
With the Lipschitz condition, we place a restriction on the behavior of functions
( )( ) ( , ) and ( )( ) ( , ) .( , ) and ( , ) are points belonging to the interval
36](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-13-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
[( ̂ )( ) , ( ̂ )( ) ] . It is to be noted that ( )( ) ( , ) is uniformly continuous. In the eventuality of
the fact, that if ( ̂ )( )
= 1 then the function ( )( ) ( , ) , the first augmentation coefficient would
be absolutely continuous.
Definition of ( ̂ )( ) , ( ̂ )( ) : 37
(D) ( ̂ )( ) , ( ̂ )( ) , are positive constants
( )( ) ( )( )
, 1
( ̂ )( ) ( ̂ )( )
Definition of ( ̂ )( ) , ( ̂ )( ) : 38
(E) There exists two constants ( ̂ ) ( )
and ( ̂ ) ( )
which together with
( ̂ )( ) , ( ̂ )( ) , ( ̂ )( )
( ̂ )( )
and the constants
( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) , = 1 ,14,15,
satisfy the inequalities
( )( )
( )( )
( ̂ )( )
( ̂ )( ) ( ̂ )( )
1
( ̂ )( )
( )( )
( )( )
(̂ )( )
( ̂ )( )
(̂ )( )
1
( ̂ )( )
Where we suppose
(F) ( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( )
0, , = 16,1 ,1 39
(G) The functions ( )( ) , ( )( ) are positive continuous increasing and bounded. 40
Definition of (p )( ) , (r )( ) :
( )
( )( ) ( , ) ( )( )
( ̂ ) 41
( )( ) ( , ) ( )( )
( )( )
( ̂ )( ) 42
(H) lim ( )( ) ( , ) = ( )( ) 43
lim ( )( ) (( ), ) = ( )( ) 44
Definition of ( ̂ )( ) , ( ̂ )( ) :
Where ( ̂ )( ) , ( ̂ )( ) , ( )( ) , ( )( ) are positive constants and = 16,1 ,1
They satisfy Lipschitz condition:
)( )
|( )( ) ( , ) ( )( ) ( , )| (̂ )( ) | | ( ̂ 45
)( )
|( )( ) (( ), ) ( )( ) (( ), )| (̂ )( ) ||( ) ( ) || ( ̂ 46
With the Lipschitz condition, we place a restriction on the behavior of functions ( )( ) ( , )
and( )( ) ( , ) .( , ) and ( , ) are points belonging to the interval [( ̂ )( ) , ( ̂ )( ) ] . It is
to be noted that ( )( ) ( , ) is uniformly continuous. In the eventuality of the fact, that if ( ̂ )( )
=
1 then the function ( )( ) ( , ) , the SECOND augmentation coefficient would be absolutely
continuous.
Definition of ( ̂ )( ) , ( ̂ )( ) :
(I) ( ̂ )( ) , ( ̂ )( ) , are positive constants 47
37](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-14-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
( )( ) ( )( )
, 1
( ̂ )( ) ( ̂ )( )
Definition of ( ̂ )( ) , ( ̂ )( ) :
There exists two constants ( ̂ )( )
and ( ̂ )( )
which together
with ( ̂ )( ) , ( ̂ )( ) , ( ̂ )( )
( ̂ )( )
and the constants
( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) , = 16,1 ,1 ,
satisfy the inequalities
( )( )
( )( )
( ̂ )( )
( ̂ )( ) ( ̂ )( )
1 48
( ̂ )( )
( )( )
( )( )
(̂ )( )
( ̂ )( )
(̂ )( )
1 49
( ̂ )( )
Theorem 1: if the conditions IN THE FOREGOING above are fulfilled, there exists a solution satisfying 50
the conditions
Definition of (0) , (0) :
( ) ( ̂ )( )
( ) ( ̂ ) , (0) = 0
) ( ̂ )( )
( ) ( ̂ )( , (0) = 0
if the conditions IN THE FOREGOING above are fulfilled, there exists a solution satisfying the 51
conditions
Definition of (0) , (0)
) ( ̂ )( )
( ) ( ̂ )( , (0) = 0
) ( ̂ )( )
( ) ( ̂ )( , (0) = 077
PROOF: 52
( )
Consider operator defined on the space of sextuples of continuous functions ,
which satisfy
(0) = , (0) = , ( ̂ )( ) , ( ̂ )( ) , 53
) ( ̂ )( )
0 ( ) ( ̂ )( 54
) ( ̂ )( )
0 ( ) ( ̂ )( 55
By 56
̅ ( )= ∫ [( )( )
( ( )) (( )( )
)( ) ( ( ( ) ), ( ) )) ( ( ) )] ( )
̅ ( )= ∫ [( )( )
( ( )) (( )( )
( )( ) ( ( ( ) ), ( ) )) ( ( ) )] ( )
57
̅ ( )= ∫ [( )( )
( ( )) (( )( )
( )( ) ( ( ( ) ), ( ) )) ( ( ) )] ( )
58
̅ ( )= ∫ [( )( )
( ( )) (( )( )
( )( ) ( ( ( ) ), ( ) )) ( ( ) )] ( )
59
̅ ( )= ∫ [( )( )
( ( )) (( )( )
( )( ) ( ( ( ) ), ( ) )) ( ( ) )] ( )
60
̅
T (t) = T ∫ [( )( )
( ( )) (( )( )
( )( ) ( ( ( ) ), ( ) )) ( ( ) )] ( )
61
Where ( ) is the integrand that is integrated over an interval (0, )
( )
Consider operator defined on the space of sextuples of continuous functions ,
38](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-15-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
which satisfy
(0) = , (0) = , ( ̂ )( ) , ( ̂ )( ) , 62
) ( ̂ )( )
0 ( ) ( ̂ )( 63
) ( ̂ )( )
0 ( ) ( ̂ )( 64
By 65
̅ ( )= ∫ [( )( )
( ( )) (( )( )
)( ) ( ( ( ) ), ( ) )) ( ( ) )] ( )
̅ ( )= ∫ [( )( )
( ( )) (( )( )
( )( ) ( ( ( ) ), ( ) )) ( ( ) )] ( )
66
̅ ( )= ∫ [( )( )
( ( )) (( )( )
( )( ) ( ( ( ) ), ( ) )) ( ( ) )] ( )
67
̅ ( )= ∫ [( )( )
( ( )) (( )( )
( )( ) ( ( ( ) ), ( ) )) ( ( ) )] ( )
68
̅ ( )= ∫ [( )( )
( ( )) (( )( )
( )( ) ( ( ( ) ), ( ) )) ( ( ) )] ( )
69
̅ ( )= ∫ [( )( )
( ( )) (( )( )
( )( ) ( ( ( ) ), ( ) )) ( ( ) )] ( )
70
Where ( ) is the integrand that is integrated over an interval (0, )
( ) 71
(a) The operator maps the space of functions satisfying CONCATENATED EQUATIONS into
itself .Indeed it is obvious that
) ( ̂ )( ) (
( ) ∫ [( )( ) ( ( ̂ )( ) )] ( ) =
( )( ) ( ̂ )( ) )( )
(1 ( )( )
) ( (̂ 1)
( ̂ )( )
From which it follows that 72
(̂ )( )
( )( ) ( )
( ̂ )( ) ̂ )(
( ( ) ) ) [((
)
) ( ̂ )( ) ]
( ̂ )(
( ) is as defined in the statement of theorem 1
Analogous inequalities hold also for , , , ,
( )
(b) The operator maps the space of functions satisfying GLOBAL EQUATIONS into
itself .Indeed it is obvious that
) ( ̂ )( ) (
( ) ∫ [( )( ) ( ( ̂ )( ) )] ( ) = 73
( )( ) ( ̂ )( ) )( )
(1 ( )( )
) ( (̂ 1)
( ̂ )( )
From which it follows that 74
(̂ )( )
( )( ) ( )
( ̂ )( ) ̂ )(
( ( ) ) [(( )
) ( ̂ )( ) ]
( ̂ )( )
Analogous inequalities hold also for , , , ,
( )( ) ( )( ) 75
It is now sufficient to take , 1 and to choose
( ̂ )( ) ( ̂ )( )
( ̂ )( ) and ( ̂ )( )
large to have
39](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-16-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
(̂ )( ) 76
( )
( )( )
[( ̂ ) ( )
(( ̂ )( )
) ] ( ̂ )( )
( ̂ )( )
(̂ )( ) 77
( )
( )( )
[(( ̂ ) ( )
) ( ̂ ) ( )
] ( ̂ ) ( )
( ̂ )( )
( )
In order that the operator transforms the space of sextuples of functions , satisfying GLOBAL
EQUATIONS into itself
( ) 78
The operator is a contraction with respect to the metric
( ) ( ) ( ) ( )
(( , ), ( , )) =
( )
( ) ( )
( )| (̂ )( ) ( )
( ) ( )
( )| (̂ )( )
| , |
Indeed if we denote 79
Definition of ̃ , ̃ : ( ̃, ̃ ) = ( )
( , )
It results
( ) ̃ ( )| ( ) ( ) (̂ )( ) ( (̂ )( ) (
|̃ ∫( )( ) | | ) )
( )
( ) ( ) (̂ )( ) (̂ )( )
∫ ( )( ) | | ( ) ( )
( ) ( ) ( ) (̂ )( ) ( (̂ )( ) (
( )( ) ( , ( ) )| | ) )
( ) ( ) ( ) (̂ )( ) ( (̂ )( ) (
|( )( ) ( , ( )) ( )( ) ( , ( ) )|
) )
( )
Where ( ) represents integrand that is integrated over the interval 0, t
From the hypotheses it follows
( ) ( ) (̂ )( ) 80
| |
(( )( )
( )( )
( ̂ )( )
( ̂ )( ) ( ̂ )( ) ) (( ( )
, ( ) ( )
, ( )
))
(̂ )( )
And analogous inequalities for . Taking into account the hypothesis the result follows
Remark 1: The fact that we supposed ( )( ) and ( )( ) depending also on t can be considered as not 81
conformal with the reality, however we have put this hypothesis ,in order that we can postulate condition
) (̂ )( ) ) (̂ )( )
necessary to prove the uniqueness of the solution bounded by ( ̂ )( ( ̂ )(
respectively of .
If instead of proving the existence of the solution on , we have to prove it only on a compact then it
suffices to consider that ( )( ) and ( )( ) , = 1 ,14,15 depend only on T and respectively on
( ) and hypothesis can replaced by a usual Lipschitz condition.
Remark 2: There does not exist any where ( )=0 ( )=0 82
From 19 to 24 it results
[ ∫ {( )( ) ( )( ) ( ( ( ) ), ( ) )} )]
( ) (
0
( ) ( ( )( ) )
0 for t 0
Definition of (( ̂ ) ( )
) , (( ̂ ) ( )
) (( ̂ )( ) ) : 83
40](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-17-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
Remark 3: if is bounded, the same property have also . indeed if
( ̂ )( ) it follows (( ̂ )( ) ) ( )( )
and by integrating
(( ̂ )( ) ) = 2( )( ) (( ̂ )( ) ) ( )( )
In the same way , one can obtain
(( ̂ )( ) ) = 2( )( ) (( ̂ )( ) ) ( )( )
If is bounded, the same property follows for , and , respectively.
Remark 4: If bounded, from below, the same property holds for . The proof is 84
analogous with the preceding one. An analogous property is true if is bounded from below.
( )
Remark 5: If T is bounded from below and lim (( ) ( ( ), )) = ( )( ) then . 85
Definition of ( )( ) and :
Indeed let be so that for
( )( )
( )( ) ( ( ), ) , ( ) ( )( )
Then ( )( ) ( )( )
which leads to 86
( )( ) ( )( )
( ) (1 ) If we take t such that = it results
( )( ) ( )( )
( ), = By taking now sufficiently small one sees that T is unbounded.
The same property holds for if lim ( )( ) ( ( ), ) = ( )( )
We now state a more precise theorem about the behaviors at infinity of the solutions OF THE GLOBAL
SYSTEM
( )( ) ( )( ) 87
It is now sufficient to take , 1 and to choose
( ̂ )( ) ( ̂ )( )
( ̂ )( )
( ̂ )( )
large to have
(̂ )( ) 88
( )
( )( )
[( ̂ )( )
(( ̂ )( )
) ] ( ̂ )( )
( ̂ )( )
(̂ )( ) 89
( )
( )( )
[(( ̂ )( )
) ( ̂ ) ( )
] ( ̂ ) ( )
(̂ )( )
( )
In order that the operator transforms the space of sextuples of functions , satisfying GLOBAL
EQUATIONS into itself
( ) 90
The operator is a contraction with respect to the metric
((( )( ) , ( )( ) ), (( )( ) , ( )( ) )) =
( )
( ) ( )
( )| (̂ )( ) ( )
( ) ( )
( )| (̂ )( )
| , |
Indeed if we denote 91
Definition of ̃ , ̃ : ( ̃, ̃ )= ( )
( , )
It results 92
( ) ̃ ( )| ( ) ( ) (̂ )( ) ( (̂ )( ) (
|̃ ∫( )( ) | | ) )
( )
41](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-18-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
( ) ( ) (̂ )( ) ( (̂ )( ) (
∫ ( )( ) | | ) )
( ) ( ) ( ) (̂ )( ) ( (̂ )( ) (
( )( ) ( , ( ) )| | ) )
( ) ( ) ( ) (̂ )( ) ( (̂ )( ) (
|( )( ) ( , ( )) ( )( ) ( , ( ) )|
) )
( )
Where ( ) represents integrand that is integrated over the interval 0,
From the hypotheses it follows
)( )
( )( ) |e (̂ )( ) 93
|(
(( )( )
( )( )
( ̂ )(
A )
( ̂ )( ) ( ̂ )( ) )d ((( )( ) , ( )( )
( )( ) , ( )( ) ))
(̂ )( )
And analogous inequalities for G and T . Taking into account the hypothesis the result follows
Remark 1: The fact that we supposed ( )( ) and ( )( ) depending also on t can be considered as not 94
conformal with the reality, however we have put this hypothesis ,in order that we can postulate condition
̂ )( ) ̂ )( )
necessary to prove the uniqueness of the solution bounded by ( ̂ )( ) e( and ( ̂ )( ) e(
respectively of .
If instead of proving the existence of the solution on , we have to prove it only on a compact then it
( ) ( )
suffices to consider that ( ) and ( ) , = 16,1 ,1 depend only on T and respectively on
( )(and not on t) and hypothesis can replaced by a usual Lipschitz condition.
Remark 2: There does not exist any t where G (t) = 0 and T (t) = 0 95
From 19 to 24 it results
)( ) ( )( ) (
G (t) G e[ ∫ {( ( ( ) ), ( ) )} ( )]
0
)( ) )
T (t) T e( (
0 for t 0
Definition of (( ̂ )( ) ) , (( ̂ )( ) ) and (( ̂ )( ) ) :
M M M 96
Remark 3: if G is bounded, the same property have also G and G . indeed if
G ( ̂ )( ) it follows
M (( ̂ )( ) )
M ( )( ) G and by integrating
G (( ̂ )( ) ) = G
M 2( )( ) (( ̂ )( ) ) (
M )( )
In the same way , one can obtain
G (( ̂ )( ) ) = G
M 2( )( ) (( ̂ )( ) ) (
M )( )
If G or G is bounded, the same property follows for G ,G and G ,G respectively.
Remark 4: If G is bounded, from below, the same property holds for G and G . The proof is 97
analogous with the preceding one. An analogous property is true if G is bounded from below.
Remark 5: If T is bounded from below and lim (( )( ) (( )(t), t)) = ( )( ) then T . 98
Definition of ( )( ) and :
Indeed let t be so that for t t
( )( )
( )( ) (( )(t), t) , T (t) ( )( )
Then ( )( ) ( ) ( )
T which leads to 99
( )( ) ( )( )
T ( ) (1 e ) T e If we take t such that e = it results
42](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-19-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
( )( ) ( )( ) 100
T ( ), = log By taking now sufficiently small one sees that T is unbounded.
The same property holds for T if lim ( )( ) (( )(t), t) = ( )( )
We now state a more precise theorem about the behaviors at infinity of the solutions
Behavior of the solutions OF THE GLOBAL SYSTEM: 101
Theorem 2: If we denote and define
Definition of ( )( ) , ( )( ) , ( )( ) , ( )( ) :
(a) )( ) , ( )( ) , ( )( ) , ( )( )
four constants satisfying
( )( )
( )( )
( )( )
( )( ) ( , ) ( )( ) ( , ) ( )( )
( )( )
( )( )
( )( )
( )( ) ( , ) ( )( ) ( , ) ( )( )
Definition of ( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )
, ( )
: 102
(b) By ( )( )
0 , ( )( )
0 and respectively ( )( )
0,( )( )
0 the roots of the
equations ( )( ) ( ( )
) ( )( ) ( )
( )( )
= 0 and ( )( ) ( ( )
) ( )( ) ( )
( )( )
=0
Definition of ( ̅ )( ) , , ( ̅ )( ) , ( ̅ )( ) , ( ̅ )( ) : 103
By ( ̅ )( )
0 , ( ̅ )( )
0 and respectively ( ̅ )( )
0 , ( ̅ )( )
0 the roots of the equations
( )( ) ( ( )
) ( )( ) ( )
( )( )
= 0 and ( )( ) ( ( )
) ( )( ) ( )
( )( )
=0
Definition of ( )( ) , ( )( ) , ( )( ) , ( )( ) , ( )( ) :- 104
(c) If we define ( )( ) , ( )( ) , ( )( ) , ( )( )
by
( ) ( ) ( ) ( ) ( )
( ) =( ) ,( ) =( ) , ( ) ( )( )
( )( )
= ( )( ) , ( )( )
= ( ̅ )( ) , ( )( )
( )( )
( ̅ )( ) ,
and ( )( )
=
( )( )
= ( )( ) , ( )( )
= ( )( ) , ( ̅ )( )
( )( )
and analogously 105
( ) ( ) ( ) ( ) ( ) ( )
( ) =( ) ,( ) =( ) , ( ) ( )
( )( )
=( )( ) , ( )( )
= ( ̅ )( ) , ( )( )
( )( )
( ̅ )( ) ,
and ( )( )
=
( )( )
=( )( ) , ( )( )
=( )( ) , ( ̅ )( )
( )( )
where ( )( ) , ( ̅ )( )
are defined respectively
Then the solution of GLOBAL CONCATENATED EQUATIONS satisfies the inequalities 106
(( )( ) ( )( ) ) ( )( )
( )
where ( )( ) is defined
(( )( ) ( )( ) ) ( )( )
( )
( )( ) ( )( )
( )( ) (( )( ) ( )( ) ) ( )( ) ( )( ) 107
( [ ] ( )
( )( ) (( )( ) ( )( ) ( )( ) )
( )( ) ( )( ) ( )( ) ( )( )
)
( )( ) (( )( ) ( )( ) )
43](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-20-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
( )( ) (( )( ) ( )( ) ) 108
( )
( )( ) (( )( ) ( )( ) ) 109
( )
( )( ) ( )( )
( )( ) ( )( ) ( )( ) ( )( ) 110
[ ] ( )
( )( ) (( )( ) ( )( ) )
( )( ) (( )( ) ( )( ) ) ( )( ) ( )( )
[ ]
( )( ) (( )( ) ( )( ) ( )( ) )
Definition of ( )( ) , ( )( ) , ( )( ) , ( )( ) :- 111
Where ( )( )
=( )( ) ( )( )
( )( )
( )( )
=( )( )
( )( )
( )( )
=( )( ) ( )( )
( )( )
( )( )
=( )( )
( )( )
Behavior of the solutions of GLOBAL EQUATIONS 112
If we denote and define
Definition of ( )( ) , ( )( ) , ( )( ) , ( )( ) : 113
( ) ( ) ( ) ( )
(d) ) ,( ) ,( ) ,( ) four constants satisfying
( )( )
( )( )
( )( )
( )( ) (T , ) ( )( ) (T , ) ( )( ) 114
( )( )
( )( )
( )( )
( )( ) (( ), ) ( )( ) (( ), ) ( )( ) 115
Definition of ( )( ) , ( )( ) , ( )( ) , ( )( ) : 116
By ( )( )
0 , ( )( )
0 and respectively ( )( )
0 ,( )( )
0 the roots
(e) of the equations ( )( ) ( ( )
) ( )( ) ( )
( )( )
=0 117
and ( )( ) ( ( )
) ( )( ) ( )
( )( )
= 0 and 118
Definition of ( ̅ )( ) , , ( ̅ )( ) , ( ̅ )( ) , ( ̅ )( ) : 119
By ( ̅ )( )
0 , ( ̅ )( )
0 and respectively ( ̅ )( )
0 , ( ̅ )( )
0 the 120
roots of the equations ( )( ) ( ( )
) ( )( ) ( )
( )( )
=0 121
and ( )( ) ( ( )
) ( )( ) ( )
( )( )
=0 122
Definition of ( )( ) , ( )( ) , ( )( ) , ( )( ) :- 123
(f) If we define ( )( ) , ( )( ) , ( )( ) , ( )( )
by 124
( )( )
= ( )( ) , ( )( )
= ( )( ) , ( )( )
( )( ) 125
( )( )
= ( )( ) , ( )( )
= ( ̅ )( ) , ( )( )
( )( )
( ̅ )( ) , 126
and ( )( )
=
( )( )
= ( )( ) , ( )( )
= ( )( ) , ( ̅ )( )
( )( ) 127
and analogously 128
( ) ( ) ( ) ( ) ( ) ( )
( ) =( ) ,( ) =( ) , ( ) ( )
( )( )
=( )( ) , ( )( )
= ( ̅ )( ) , ( )( )
( )( )
( ̅ )( ) ,
44](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-21-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
and ( )( )
=
( )( )
= ( )( ) , ( )( )
=( )( ) , ( ̅ )( )
( )( ) 129
Then the solution of GLOBAL EQUATIONS satisfies the inequalities 130
)( ) ( )( ) ) )( )
G e(( ( ) G e(
( )( ) is defined
)( ) ( )( ) ) )( )
G e(( ( ) G e( 131
( )( ) ( )( )
( )( ) (( )( ) ( )( ) ) ( )( ) ( )( ) 132
( [e e ] G e G ( )
( )( ) (( )( ) ( )( ) ( )( ) )
( )( ) )( ) )( ) )( )
e( e (
G e (
)
( )( ) (( )( ) ( )( ) )
)( ) )( ) ( )( ) ) 133
T e( ( ) T e((
)( ) )( ) ( )( ) )
T e( ( ) T e(( 134
( )( ) ( )( )
( )( ) ( )( ) ( )( ) ( )( ) 135
[e e ] T e ( )
( )( ) (( )( ) ( )( ) )
( )( ) )( ) ( )( ) ) )( ) )( )
[e(( e (
] T e (
( )( ) (( )( ) ( )( ) ( )( ) )
Definition of ( )( ) , ( )( ) , (R )( ) , (R )( ) :- 136
Where ( )( )
=( )( ) ( )( )
( )( ) 137
( )( )
=( )( )
( )( )
( )( )
=( )( ) ( ) ( )
( )( )
(R )( )
=( )( )
( )( )
PROOF : From GLOBAL EQUATIONS we obtain 138
( )
=( )( )
(( )( )
( )( )
( )( ) ( , )) ( )( ) ( , ) ( )
( )( ) ( )
( ) ( )
Definition of :- =
It follows
( )
(( )( ) ( ( )
) ( )( ) ( )
( )( ) ) (( )( ) ( ( )
) ( )( ) ( )
( )( ) )
From which one obtains
Definition of ( ̅ )( ) , ( )( ) :-
(a) For 0 ( )( )
= ( )( )
( ̅ )( )
[ ( )( ) (( )( ) ( )( ) ) ]
( ) ( )( ) ( )( ) ( )( ) ( )( ) ( )( )
( ) )( ) (( )( ) ( )( ) ) ]
, ( )( )
=
[ ( ( )( ) ( )( )
( )( )
it follows ( )( ) ( )
( ) ( )( )
In the same manner , we get 139
[ ( )( )((̅ )( ) (̅ )( ) ) ]
(̅ )( ) ( ̅ )( ) (̅ )( ) (̅ )( ) ( )( )
( )
( ) )( )((̅ )( ) (̅ )( ) ) ]
, ( ̅ )( )
=
[ ( ( )( ) (̅ )( )
( ̅ )( )
45](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-22-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
From which we deduce ( )( ) ( )
( ) ( ̅ )( )
(b) If 0 ( )( )
( )( )
= ( ̅ )( )
we find like in the previous case, 140
[ ( )( ) (( )( ) ( )( ) ) ]
( )( ) ( )( ) ( )( )
( )( )
[ ( )( ) (( )( ) ( )( ) ) ]
( )
( )
( )( )
[ ( )( )((̅ )( ) (̅ )( ) ) ]
(̅ )( ) ( ̅ )( ) (̅ )( )
[ ( )( )((̅ )( ) (̅ )( ) ) ]
( ̅ )( )
( ̅ )( )
141
(c) If 0 ( )( )
( ̅ )( )
( )( )
= , we obtain
[ ( )( ) ((̅ )( ) (̅ )( )) ]
(̅ )( ) ( ̅ )( ) (̅ )( )
( )( ) ( )
( ) [ ( )( ) ((̅ )( ) (̅ )( )) ]
( )( )
( ̅ )( )
And so with the notation of the first part of condition (c) , we have
( )
Definition of ( ) :-
( )
( )( ) ( )
( ) ( )( ) , ( )
( )=
( )
In a completely analogous way, we obtain
( )
Definition of ( ) :-
( )
( )( ) ( )
( ) ( )( ) , ( )
( )=
( )
Now, using this result and replacing it in CONCATENATED SYSTEM OF EQUATIONS we get easily
the result stated in the theorem.
Particular case :
If ( )( )
=( )( ) , ( )( )
= ( )( )
and in this case ( )( )
= ( ̅ )( )
if in addition ( )( )
=
( )( ) then ( )
( ) = ( )( ) and as a consequence ( ) = ( )( )
( ) this also defines ( )( )
for
the special case
Analogously if ( )( )
=( )( ) , ( )( )
= ( )( ) and then
( )( )
= ( ̅ )( ) if in addition ( )( )
= ( )( )
then ( )=( )( )
( ) This is an important
consequence of the relation between ( )( ) and ( ̅ )( ) , and definition of ( )( ) .
PROOF : From GLOBAL EQUATIONS we obtain (PLEASE REFER PART ONE OF THE PAPER) 142
( )
=( )( )
(( )( )
( )( )
( )( ) (T , t)) ( )( ) (T , t) ( )
( )( ) ( )
( ) ( ) 143
Definition of :- =
It follows 144
( )
(( )( ) ( ( )
) ( )( ) ( )
( )( ) ) (( )( ) ( ( )
) ( )( ) ( )
( )( ) )
From which one obtains 145
Definition of ( ̅ )( ) , ( )( ) :-
(d) For 0 ( )( )
= ( )( )
( ̅ )( )
46](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-23-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
[ ( )( ) (( )( ) ( )( ) ) ]
( ) ( )( ) ( )( ) ( )( ) ( )( ) ( )( )
( ) )( ) (( )( ) ( )( ) ) ]
, ( )( )
=
[ ( ( )( ) ( )( )
( )( )
it follows ( )( ) ( )
( ) ( )( )
In the same manner , we get 146
[ ( )( ) ((̅ )( ) (̅ )( ) ) ]
(̅ )( ) ( ̅ )( ) (̅ )( ) (̅ )( ) ( )( )
( )
( ) )( ) ((̅ )( ) (̅ )( ) ) ]
, ( ̅ )( )
=
[ ( ( )( ) (̅ )( )
( ̅ )( )
From which we deduce ( )( ) ( )
( ) ( ̅ )( )
(e) If 0 ( )( )
( )( )
= ( ̅ )( )
we find like in the previous case, 147
[ ( )( ) (( )( ) ( )( ) ) ]
( )( ) ( )( ) ( )( )
( )( )
[ ( )( ) (( )( ) ( )( ) ) ]
( )
( )
( )( )
[ ( )( ) ((̅ )( ) (̅ )( ) ) ]
(̅ )( ) ( ̅ )( ) (̅ )( )
[ ( )( ) ((̅ )( ) (̅ )( ) ) ]
( ̅ )( )
( ̅ )( )
(f) If 0 ( )( )
( ̅ )( )
( )( )
= , we obtain 148
[ ( )( )((̅ )( ) (̅ )( ) ) ]
(̅ )( ) ( ̅ )( ) (̅ )( )
( )( ) ( )
( ) [ ( )( )((̅ )( ) (̅ )( ) ) ]
( )( )
( ̅ )( )
And so with the notation of the first part of condition (c) , we have
( )
Definition of ( ) :- 149
( )
( )( ) ( )
( ) ( )( ) , ( )
( )=
( )
In a completely analogous way, we obtain 150
( )
Definition of ( ) :-
( )
( )( ) ( )
( ) ( )( ) , ( )
( )=
( )
Now, using this result and replacing it in GLOBAL SOLUTIONS we get easily the result stated in the
theorem.
Particular case : 151
If ( )( )
=( )( ) , ( )( )
=( )( )
and in this case ( )( )
= ( ̅ )( )
if in addition ( )( )
=
( )( ) then ( )
( ) = ( )( ) and as a consequence ( ) = ( )( )
( )
( ) ( ) ( ) ( )
Analogously if ( ) =( ) , ( ) =( ) and then
( )( )
= ( ̅ )( ) if in addition ( )( )
= ( )( )
then ( )=( )( )
( ) This is an important
( ) ( )
consequence of the relation between ( ) and ( ̅ )
We can prove the following 152
( ) ( )
Theorem 3: If ( ) ( ) are independent on , and the conditions
( )( ) ( )( )
( )( ) ( )( )
0
( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( )
0
( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) 0,
( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( )
0
( )( ) , ( )( ) as defined are satisfied , then the system
47](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-24-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
If ( )( )
( )( ) are independent on t , and the conditions
( )( ) ( )( )
( )( ) ( )( )
0 153
( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( )
0
( )( ) ( )( )
( )( ) ( )( )
0,
( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( )
0
( ) ( )
( ) ,( ) as defined are satisfied , then the system
( )( )
[( )( )
( )( ) ( )] = 0 154
( )( )
[( )( )
( )( ) ( )] = 0 155
( )( )
[( )( )
( )( ) ( )] = 0 156
( )( )
( )( )
( )( ) ( ) = 0 157
( )( )
( )( )
( )( ) ( ) = 0 158
( )( )
( )( )
( )( ) ( ) = 0 159
has a unique positive solution , which is an equilibrium solution for the system
( )( )
[( )( )
( )( ) ( )] = 0 160
( )( )
[( )( )
( )( ) ( )] = 0 161
( )( )
[( )( )
( )( ) ( )] = 0 162
( )( )
( )( )
( )( ) ( ) = 0 163
( )( )
( )( )
( )( ) ( ) = 0 164
( )( )
( )( )
( )( ) ( ) = 0 165
has a unique positive solution , which is an equilibrium solution for the GLOBAL SYSTEM
Proof: 166
(a) Indeed the first two equations have a nontrivial solution , if
( )=( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( ) ( ) ( )( ) ( )( ) ( )
( ) ( )
( ) ( )( ) ( )=0
(a) Indeed the first two equations have a nontrivial solution , if 167
F( )=( )( ) ( )( )
( )( ) ( )( )
( )( ) ( )( ) ( ) ( )( ) ( )( ) ( )
( ) ( )
( ) ( )( ) ( )=0
Definition and uniqueness of T :- 168
( )
After hypothesis (0) 0, ( ) 0 and the functions ( ) ( ) being increasing, it follows that
there exists a unique for which ( ) = 0. With this value , we obtain from the three first
equations
( )( ) ( )( )
= , =
[( )( ) ( )( ) ( )] [( )( ) ( )( ) ( )]
48](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-25-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
Definition and uniqueness of T :- 169
( )
After hypothesis (0) 0, ( ) 0 and the functions ( ) ( ) being increasing, it follows that
there exists a unique T for which (T ) = 0. With this value , we obtain from the three first
equations
( )( ) ( )( ) 170
= , =
[( )( ) ( )( ) ( )] [( )( ) ( )( ) ( )]
(c) By the same argument, the equations(CONCATENATED SET OF THE GLOBAL SYSTEM) 171
admit solutions , if
( ) ( )
( )=( ) ( ) ( )( ) ( )( )
[( )( ) ( )( ) ( ) ( )( ) ( )( ) ( )] ( )( ) ( )( )( ) ( ) = 0
Where in ( , , ), , must be replaced by their values from 96. It is easy to see that is a
decreasing function in taking into account the hypothesis (0) 0, ( ) 0 it follows that there
exists a unique such that ( )=0
(d) By the same argument, the equations (SOLUTIONAL EQUATIONS OF THE GLOBAL 172
EQUATIONS) admit solutions , if
( )=( )( ) ( )( )
( )( ) ( )( )
[( )( ) ( )( ) ( ) ( )( ) ( )( ) ( )] ( )( ) ( )( )( ) ( )=0
Where in ( )( , , ), , must be replaced by their values from 96. It is easy to see that is 173
a decreasing function in taking into account the hypothesis (0) 0, ( ) 0 it follows that
there exists a unique G such that (( ) )=0
Finally we obtain the unique solution 174
given by ( )=0, given by ( ) = 0 and
( )( ) ( )( )
= , =
[( )( ) ( )( ) ( )] [( )( ) ( )( ) ( )]
( )( ) ( )( )
= , =
[( )( ) ( )( ) ( )] [( )( ) ( )( )( )]
Obviously, these values represent an equilibrium solution THE GLOBAL SYSTEM
G given by (( ) ) = 0 , T given by (T ) = 0 and 175
( )( ) ( )( ) 176
G = , G =
[( )( ) ( )( ) ( )] [( )( ) ( )( ) ( )]
( )( ) ( )( ) 177
T = , T =
[( )( ) ( )( ) (( ) )] [( )( ) ( )( ) (( ) )]
Obviously, these values represent an equilibrium solution of THE GLOBAL SYSTEM
ASYMPTOTIC STABILITY ANALYSIS 178
Theorem 4: If the conditions of the previous theorem are satisfied and if the functions
( )( )
( )( )
Belong to ( )
( ) then the above equilibrium point is asymptotically stable.
Proof: Denote
Definition of , :-
49](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-26-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
= , =
( )( ) ( )( )
( )=( )( )
, ( )=
Then taking into account equations GLOBAL EQUATIONS and neglecting the terms of power 2, we
obtain
= (( )( )
( )( ) ) ( )( )
( )( ) 179
= (( )( )
( )( ) ) ( )( )
( )( ) 180
= (( )( )
( )( ) ) ( )( )
( )( ) 181
= (( )( )
( )( ) ) ( )( )
∑ ( ( )( ) ) 182
= (( )( )
( )( ) ) ( )( )
∑ ( ( )( ) ) 183
= (( )( )
( )( ) ) ( )( )
∑ ( ( )( ) ) 184
If the conditions of the previous theorem are satisfied and if the functions (a )( ) and (b )( )
Belong to
( )
( ) then the above equilibrium point is asymptotically stable
Denote
Definition of , :-
G =G ,T =T 185
( )( ) ( )( ) 186
(T ) = ( )( )
, (( ) )=
taking into account equations (SOLUTIONAL EQUATIONS TO THE GLOBAL EQUATIONS) and 187
neglecting the terms of power 2, we obtain
= (( )( )
( )( ) ) ( )( )
( )( ) G 188
= (( )( )
( )( ) ) ( )( )
( )( ) G 189
= (( )( )
( )( ) ) ( )( )
( )( ) G 190
= (( )( )
( )( ) ) ( )( )
∑ ( ( )( ) T ) 192
= (( )( )
( )( ) ) ( )( )
∑ ( ( )( ) T ) 193
= (( )( )
( )( ) ) ( )( )
∑ ( ( )( ) T ) 194
The characteristic equation of this system is 195
(( )( )
( )( )
( )( ) ) (( )( )
( )( )
( )( ) )
[((( )( )
( )( )
( )( ) )( )( )
( )( ) ( )( )
)]
((( )( )
( )( )
( )( ) ) ( ),( ) ( )( )
( ),( ) )
((( )( )
( )( )
( )( ) )( )( )
( )( ) ( )( )
)
((( )( )
( )( )
( )( ) ) ( ),( ) ( )( )
( ),( ) )
((( )( ) ) (( )( )
( )( )
( )( )
( )( ) ) ( ) ( ) )
50](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-27-2048.jpg)
![Advances in Physics Theories and Applications www.iiste.org
ISSN 2224-719X (Paper) ISSN 2225-0638 (Online)
Vol 6, 2012
((( )( ) ) (( )( )
( )( )
( )( )
( )( ) ) ( ) ( ) )
((( )( ) ) (( )( )
( )( )
( )( )
( )( ) ) ( ) ( ) ) ( )( )
(( )( )
( )( )
( )( ) ) (( )( ) ( )( )
( )( ) ( )( ) ( )( )
)
((( )( )
( )( )
( )( ) ) ( ),( ) ( )( )
( ),( ) ) =0
+
(( )( )
( )( )
( )( ) ) (( )( )
( )( )
( )( ) )
[((( )( )
( )( )
( )( ) )( )( ) G ( )( ) ( )( ) G )]
((( )( )
( )( )
( )( ) ) ( ),( )T ( )( )
( ),( )T )
((( )( )
( )( )
( )( ) )( )( ) G ( )( ) ( )( ) G )
((( )( )
( )( )
( )( ) ) ( ),( )T ( )( )
( ),( )T )
((( )( ) ) (( )( )
( )( )
( )( )
( )( ) ) ( ) ( ) )
((( )( ) ) (( )( )
( )( )
( )( )
( )( ) ) ( )( ) )
((( )( ) ) (( )( )
( )( )
( )( )
( )( ) ) ( ) ( ) ) ( )( ) G
(( )( )
( )( )
( )( ) ) (( )( ) ( )( ) G ( )( ) ( )( ) ( )( ) G )
((( )( )
( )( )
( )( ) ) ( ),( )T ( )( )
( ),( )T ) =0
And as one sees, all the coefficients are positive. It follows that all the roots have negative real part, and
this proves the theorem.
Acknowledgments:
The introduction is a collection of information from various articles, Books, News Paper reports, Home
Pages Of authors, Article Abstracts, NASA PAGES FOR FIGURES, STANFORD ENCYCLOPEDIA,
NATURE review articles, Face Book appraisals for the common man, ask a physicist column, Journal
Reviews, the internet including Wikipedia. We acknowledge all authors who have contributed to the
same. In the eventuality of the fact that there has been any act of omission on the part of the authors, We
regret with great deal of compunction, contrition, and remorse. As Newton said, it is only because erudite
and eminent people allowed one to piggy ride on their backs; probably an attempt has been made to look
slightly further. Once again, it is stated that the references are only illustrative and not comprehensive
REFERENCES
2. A Haimovici: “On the growth of a two species ecological system divided on age groups”. Tensor,
Vol 37 (1982),Commemoration volume dedicated to Professor Akitsugu Kawaguchi on his 80 th
birthday
3. Fritjof Capra: “The web of life” Flamingo, Harper Collins See "Dissipative structures” pages 172-188
4. Heylighen F. (2001): "The Science of Self-organization and Adaptivity", in L. D. Kiel, (ed) .
Knowledge Management, Organizational Intelligence and Learning, and Complexity, in: The
Encyclopedia of Life Support Systems ((EOLSS), (Eolss Publishers, Oxford) [http://www.eolss.net
51](https://image.slidesharecdn.com/decoheringenvironmentandcoupledquantumstatesandinternalresonanceincoupledspinsystems-120705023230-phpapp01/75/Decohering-environment-and-coupled-quantum-states-and-internal-resonance-in-coupled-spin-systems-28-2048.jpg)


