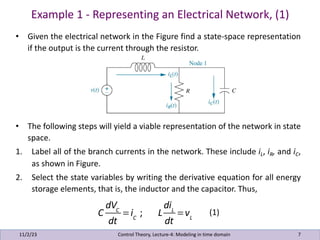
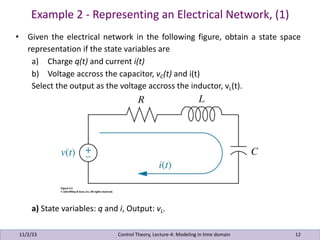
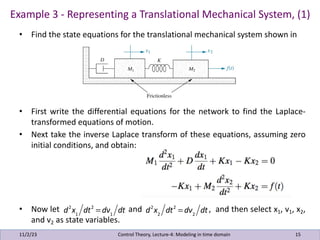
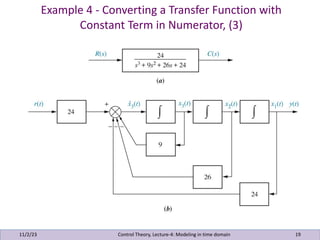
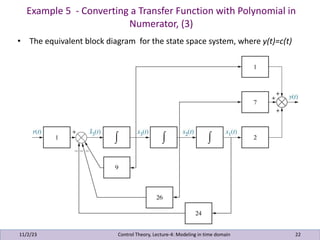
This document presents lecture notes on control theory, specifically focusing on modeling in the time domain. It discusses two main approaches: the classical frequency-domain technique and the state-space approach, which is useful for a variety of systems including nonlinear and time-varying systems. Several examples illustrate how to represent electrical networks and translational mechanical systems in state-space form, along with methods to derive output equations and convert state-space representations to transfer functions.