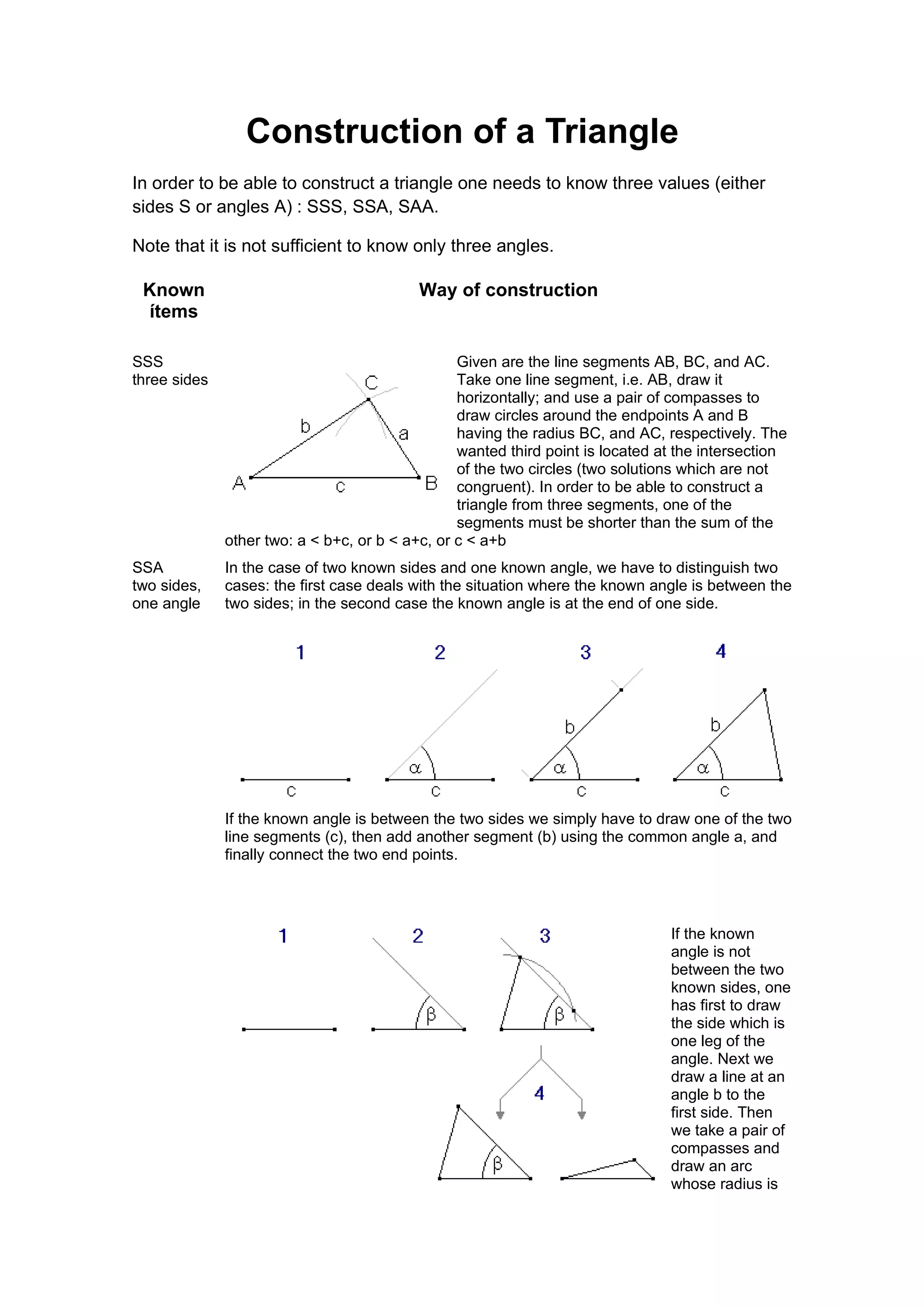
To construct a triangle, you need to know three pieces of information: three side lengths (SSS), two side lengths and the angle between them (SSA), or one side length and the two angles adjacent to it (SAA). For each case, there is a defined construction process using a compass and straightedge that allows locating the third point to complete the triangle.

1. Construction of a Triangle
In order to be able to construct a triangle one needs to know three values (either
sides S or angles A) : SSS, SSA, SAA.
Note that it is not sufficient to know only three angles.
Known Way of construction
ítems
SSS Given are the line segments AB, BC, and AC.
three sides Take one line segment, i.e. AB, draw it
horizontally; and use a pair of compasses to
draw circles around the endpoints A and B
having the radius BC, and AC, respectively. The
wanted third point is located at the intersection
of the two circles (two solutions which are not
congruent). In order to be able to construct a
triangle from three segments, one of the
segments must be shorter than the sum of the
other two: a < b+c, or b < a+c, or c < a+b
SSA In the case of two known sides and one known angle, we have to distinguish two
two sides, cases: the first case deals with the situation where the known angle is between the
one angle two sides; in the second case the known angle is at the end of one side.
If the known angle is between the two sides we simply have to draw one of the two
line segments (c), then add another segment (b) using the common angle a, and
finally connect the two end points.
If the known
angle is not
between the two
known sides, one
has first to draw
the side which is
one leg of the
angle. Next we
draw a line at an
angle b to the
first side. Then
we take a pair of
compasses and
draw an arc
whose radius is

2. the length of the second side. Finally we connect the intersection of the arc to the
starting and ending point of the first side. Note that there are usually two solutions.
If the second side is two short there could be even no solution at all.
SAA
one side,
two angles
If the two known angles are both adjacent to the known side, we simple draw the
side and construct two lines at the known angles a and b. The triangle results from
the end points of the known side and the intersection of the two lines. Please note
that in the case of two known angles, the third angle is automatically known, too
(the sum of all angles in a triangle is 180°, thus the third angle g is 180-a-b).