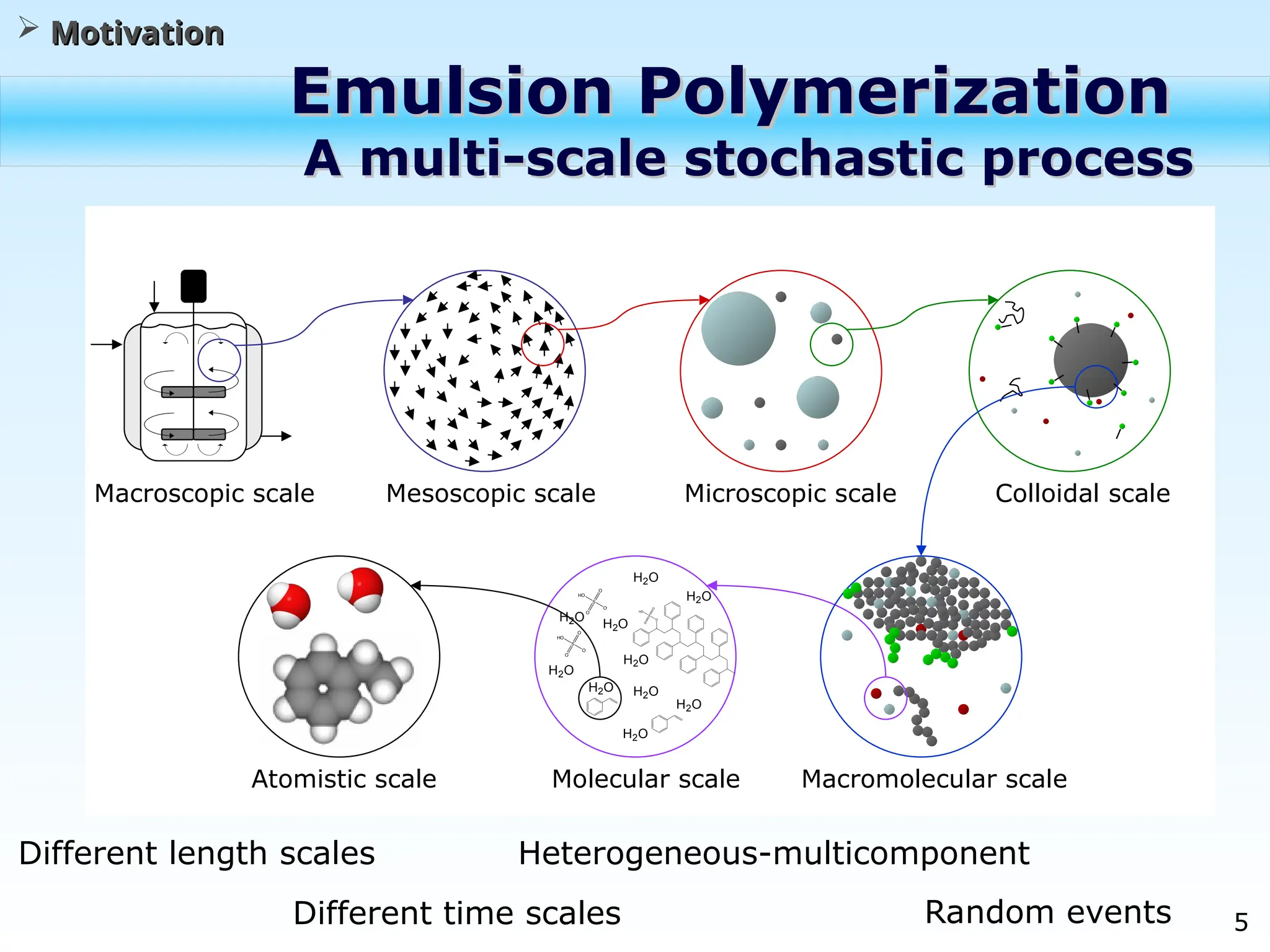
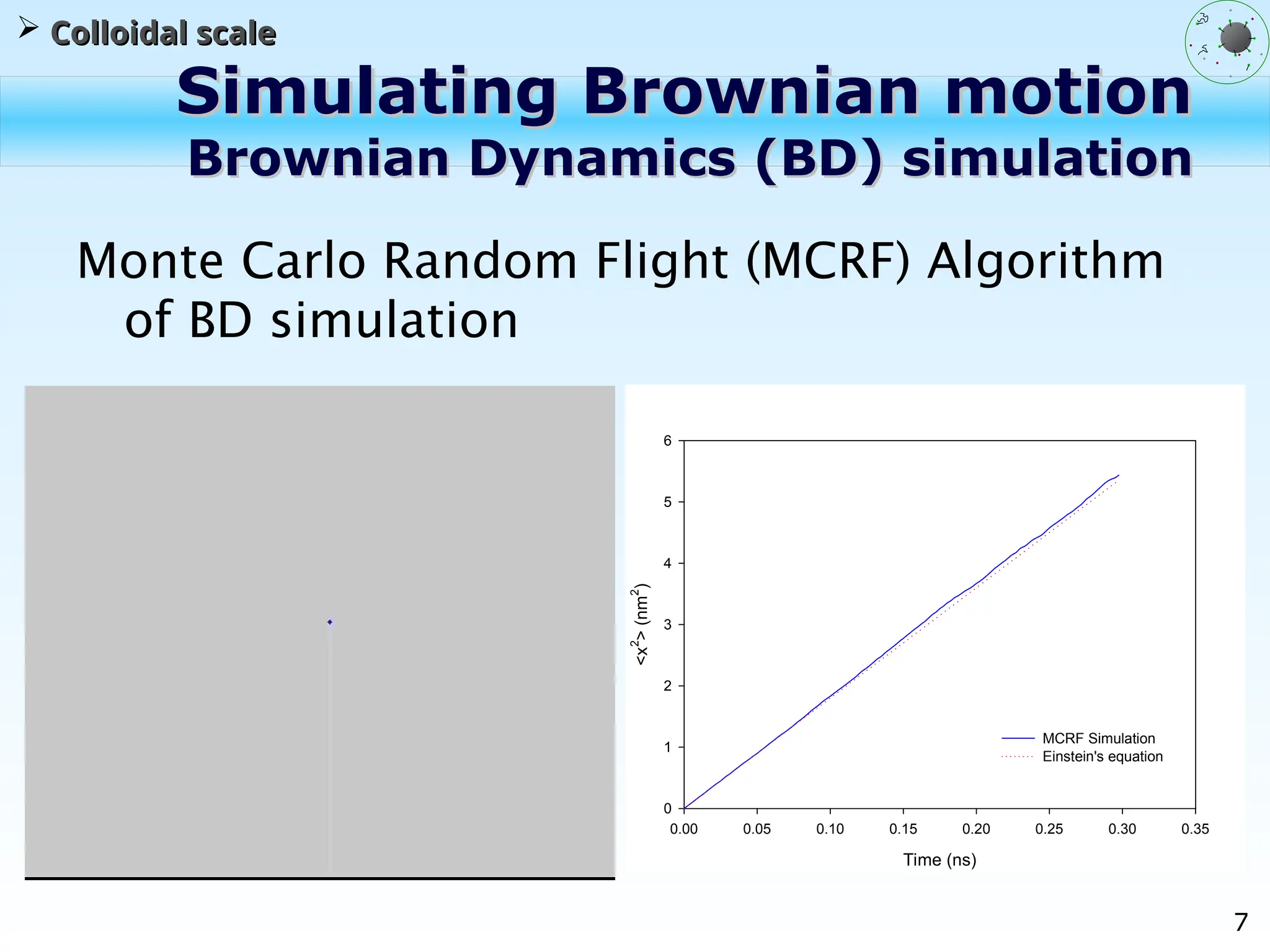
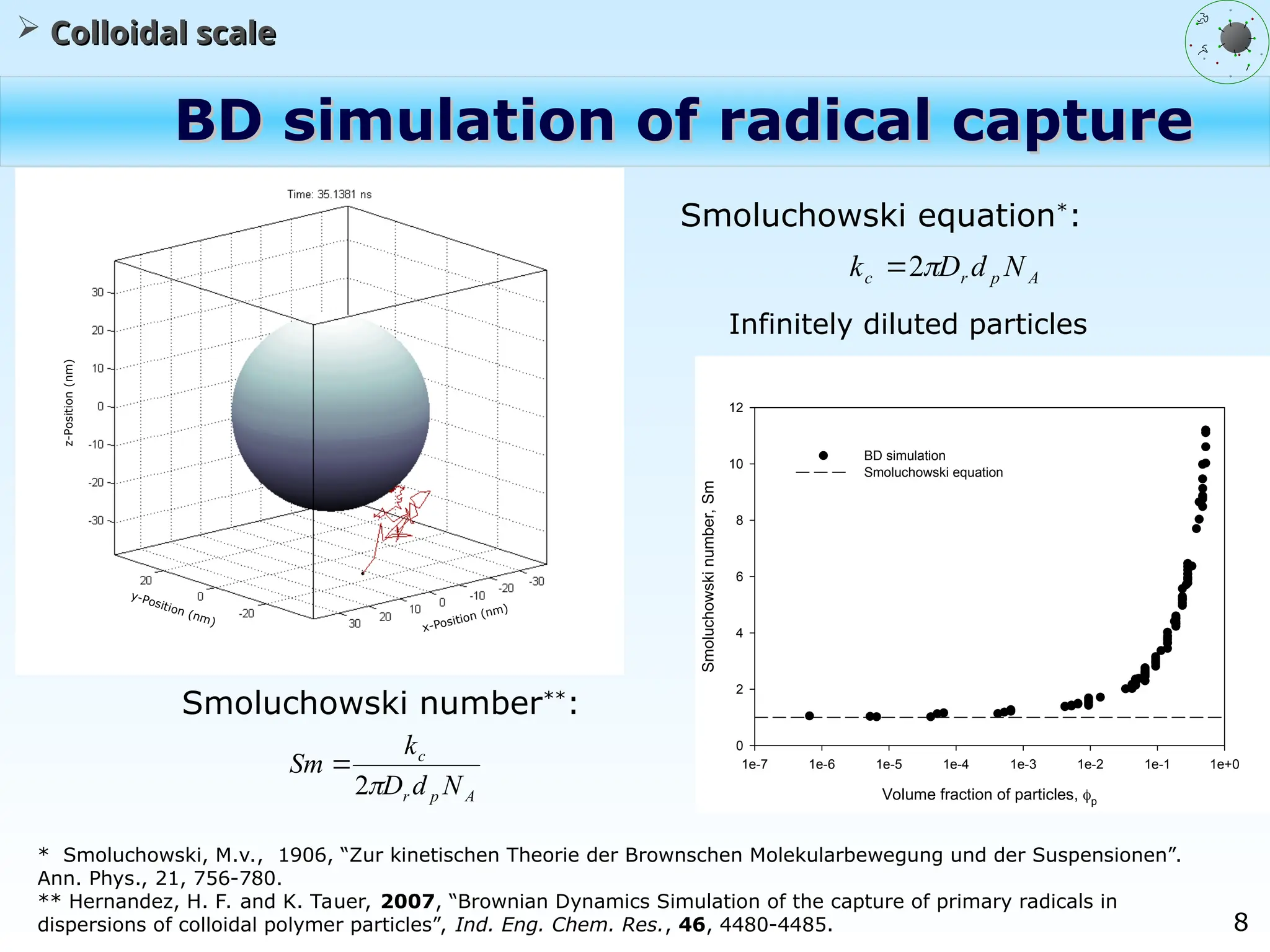
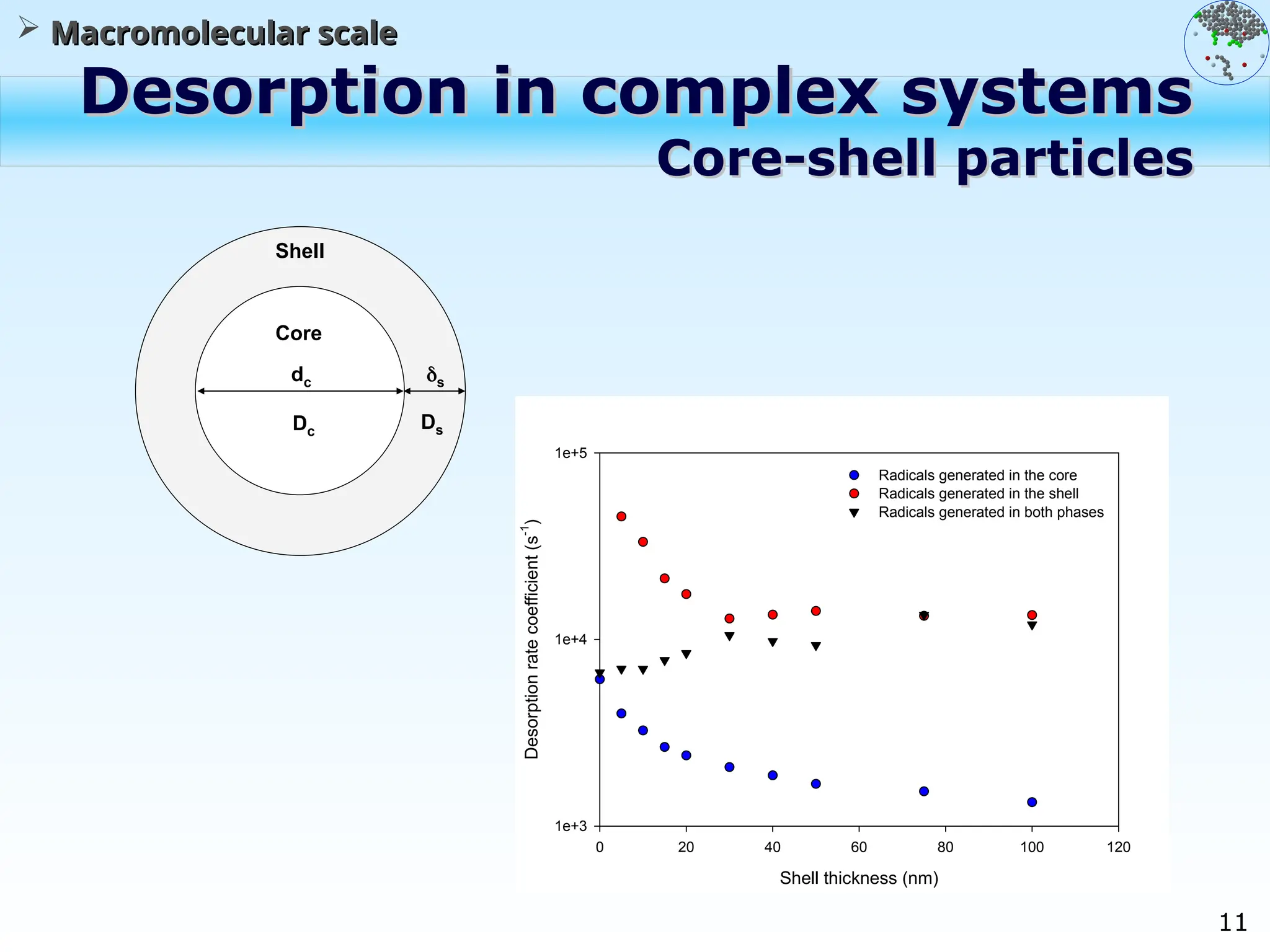
The document discusses the multiscale stochastic modeling of emulsion polymerization, highlighting the current gaps in understanding and the need for better experimental methods and models. It outlines various scales of analysis—from colloidal to macromolecular—and emphasizes the significance of integrating these scales for a comprehensive understanding of the polymerization process. Conclusively, it asserts that improving modeling and simulation across these scales is crucial for advancing knowledge in emulsion polymerization and related processes.

1. Consistent mechanism of emulsion
Consistent mechanism of emulsion
polymerization: A multiscale stochastic
polymerization: A multiscale stochastic
approach
approach
Hugo Hernandez
Polymer Dispersions Group
Colloid Chemistry Department
Max Planck Institute of Colloids and Interfaces
z-Position
(nm)
y-Position (nm)
x-Position (nm)
z-Position
(nm)
y-Position (nm)
x-Position (nm)

2. 2
Outline
Outline
• Motivation
• Colloidal scale
• Macromolecular scale
• Molecular scale
• Microscopic scale
• Multi-scale integration
• Outlook
• Acknowledgments

3. 3
Comprehensive modeling
Comprehensive modeling
• Design of polymer particles:
– Morphology
– Particle size distribution
– Molecular weight distribution
– Mechanical properties
– Stability
– Performance
• Industrial production:
– Process optimization
– Quality control
 Motivation
Motivation

4. 4
Some unresolved issues
Some unresolved issues
A complete consistent picture of emulsion
polymerization is not available.
Some controversial topics:
– Particle nucleation
– Radical capture
– Radical desorption
– Monomer swelling
Limitations:
– Lack of adequate experimental methods
– Models developed for very specific conditions
– Unreliable model discrimination
Better models and more accurate validation data are
needed!
 Motivation
Motivation

5. 5
Macroscopic scale Mesoscopic scale Microscopic scale Colloidal scale
Molecular scale
O-
S
O
O
HO
O-
S
O
O
HO
O
S
O
O
HO
H2O
H2O
H2O
H2O
H2O
H2O
H2O
H2O
H2O
H2O
Emulsion Polymerization
Emulsion Polymerization
A multi-scale stochastic process
A multi-scale stochastic process
Macromolecular scale
Atomistic scale
Different length scales
 Motivation
Motivation
Heterogeneous-multicomponent
Different time scales Random events

6. 6
Diffusion by Brownian motion
Diffusion by Brownian motion
Dt
n
x d
2
2

 Colloidal scale
Colloidal scale
Einstein’s equation of Brownian motion:
Langevin description:
nd=1,2 or 3 number of dimensions
Fick’s second law:
D: Diffusion coefficient
c
D
t
c 2




d
t
mD
kT
n
Ce
D
dt
x
d









2
2

7. 7
Simulating Brownian motion
Simulating Brownian motion
Brownian Dynamics (BD) simulation
Brownian Dynamics (BD) simulation
Monte Carlo Random Flight (MCRF) Algorithm
of BD simulation
 Colloidal scale
Colloidal scale
Time (ns)
0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35
<x
2
>
(nm
2
)
0
1
2
3
4
5
6
MCRF Simulation
Einstein's equation

8. 8
BD simulation of radical capture
BD simulation of radical capture
A
p
r
c N
d
D
k 
2

z-Position
(nm)
y-Position (nm)
x-Position (nm)
z-Position
(nm)
y-Position (nm)
x-Position (nm)
 Colloidal scale
Colloidal scale
* Smoluchowski, M.v., 1906, “Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen”.
Ann. Phys., 21, 756-780.
** Hernandez, H. F. and K. Tauer, 2007, “Brownian Dynamics Simulation of the capture of primary radicals in
dispersions of colloidal polymer particles”, Ind. Eng. Chem. Res., 46, 4480-4485.
Volume fraction of particles, p
1e-7 1e-6 1e-5 1e-4 1e-3 1e-2 1e-1 1e+0
Smoluchowski
number,
Sm
0
2
4
6
8
10
12
BD simulation
Smoluchowski equation
Smoluchowski equation*
:
Infinitely diluted particles
A
p
r
c
N
d
D
k
Sm

2

Smoluchowski number**
:

9. 9
Models of radical capture
Models of radical capture
 Colloidal scale
Colloidal scale
• Collision model: (Gardon, 1968; Fitch and Tsai, 1971)
kc  dp
2
• Diffusion model: (Ugelstad and Hansen, 1976)
kc  dp
• Colloidal model: (Penboss et al., 1983)
kc  dp
• Propagational model: (Maxwell et al., 1991)
kc  dp
0
• BD simulation: (Hernandez and Tauer, 2007)
kc  dp(1+p)
kc  dp+’Ndp
4

10. 10
Models of radical desorption
Models of radical desorption
2
0
p
p
d
D
k


 Macromolecular scale
Macromolecular scale
* Hernandez, H. F. and K. Tauer, 2008, “Radical desorption kinetics in emulsion polymerization - Theory and
Simulation”, Submitted to Ind. Eng. Chem. Res.
Theoretical model based on the 3-dimensional Einstein‘s equation*
:
Model 
Ugelstad et al. (1969) 1.542
Harada et al. (1971) 12
Friis and Nyhagen (1973) 8
Ugelstad and Hansen (1976) 12
Nomura and Harada (1981) 2
Chang, Litt and Nomura (1982) 5
Nomura (1982) 2 – 5
Asua et al. (1989) 6
Grady and Matheson (1996) 20/3
Present theoretical model 60
BD simulation results 57.14
Dp
/dp
2
(s-1
)
1e-1 1e+0 1e+1 1e+2 1e+3 1e+4 1e+5 1e+6 1e+7
k
0
(s
-1
)
1e+1
1e+2
1e+3
1e+4
1e+5
1e+6
1e+7
1e+8
1e+9
2
14
.
57
p
p
desorp
d
D
k 
=60

11. 11
Desorption in complex systems
Desorption in complex systems
Core-shell particles
Core-shell particles
Shell
Core
dc s
Dc
Ds
 Macromolecular scale
Macromolecular scale
Shell thickness (nm)
0 20 40 60 80 100 120
Desorption
rate
coefficient
(s
-1
)
1e+3
1e+4
1e+5
Radicals generated in the core
Radicals generated in the shell
Radicals generated in both phases

12. 12
Desorption in complex systems
Desorption in complex systems
Monomer concentration gradient
Monomer concentration gradient
 Macromolecular scale
Macromolecular scale
Temperature, T (K)
300 320 340 360
Diffusion
coefficient,
D
(m
2
/s)
1e-13
1e-12
1e-11
1e-10
1e-9
1e-8
BD simulation
Particle surface
Particle center
dp
wp
0.8
0 dp/2
r
Dp
10-9
10-12

13. 13
Desorption in complex systems
Desorption in complex systems
Non-spherical particles
Non-spherical particles
 Macromolecular scale
Macromolecular scale
y=1, z=1
(Sphere)
y=1, z>1
(Oblate spheroid)
y=z>1
(Prolate spheroid)
y=1, z>>1
(Thin disc)
y=z>>1
(Needle)
1e+6
1e+7
1e+8
1
10
1
10
Irreversible
desorption
rate
coefficient,
k
0
(s
-1
)
 z

y
Sphere
Needle
Thin disc
Oblate spheroids
P
r
o
l
a
t
e
s
p
h
e
r
o
i
d
s

14. 14
Intermolecular forces
Intermolecular forces
 Molecular scale
Molecular scale
The effect of intermolecular forces:
– Electrical double layer
– Interfacial tension, Laplace pressure
– Chemical potential, energy and entropy of mixing
– Flory-Huggins interaction parameters
– Maxwell-Stefan diffusion coefficients
– Non-conservative forces: Friction
– Spontaneous emulsification*
Molecular Dynamics
Monte Carlo
* Tauer, K., H. Hernandez, S. Kozempel, O. Lazareva and P. Nazaran, 2007, “Towards a consistent mechanism
of emulsion polymerization – new experimental details”, Colloid Polym. Sci., In press.
O-
S
O
O
HO
O-
S
O
O
HO
O
S
O
O
HO
H2O
H2O
H2O
H2O
H2O
H2O
H2O
H2O
H2O
H2O
O-
S
O
O
HO
O-
S
O
O
HO
O
S
O
O
HO
H2O
H2O
H2O
H2O
H2O
H2O
H2O
H2O
H2O
H2O

15. 15
Diffusion-limited reactions
Diffusion-limited reactions
Cage, gel and glass effects
Cage, gel and glass effects
 Microscopic scale
Microscopic scale
Time (s)
0 5000 10000 15000 20000 25000 30000
Conversion
0.0
0.2
0.4
0.6
0.8
1.0
HSSA-IM
HSSA
Experimental data
Cage effect
Gel effect
Glass effect
* Hernandez, H. F. and K. Tauer, 2008, “Hybrid stochastic simulation of imperfect mixing in free radical
polymerization”, Submitted to Macromol. Symp.
Bulk radical polymerization of MMA up to high conversions
Application of the hybrid stochastic simulation algorithm for imperfect
mixing (HSSA-IM)*

16. 16
Hybrid BD-kMC simulation
Hybrid BD-kMC simulation*
*
Time, t (s)
0 2000 4000 6000 8000 10000
Capture
rate
coefficient,
k
c
(l
water/part.s)
1e-12
1e-11
1e-10
BD simulation updates
 Multi-scale integration
Multi-scale integration
Aqueous phase propagation vs. capture by particles
Particle diameter, dp (nm)
0 100 200 300 400 500 600
L
n
,
L
w
,
PDI
1
2
3
4
5
L
max
0.1
1
10
100
Weight average chain length, Lw
Polydispersity index, PDI
Number average chain length, Ln
Max. chain length, Lmax
Seed volume fraction: 1%
* Hernandez, H. F. and K. Tauer, 2007, “Brownian Dynamics and Kinetic Monte Carlo Simulation in Emulsion
Polymerization”, Accepted in 18th European Symposium on Computer Aided Process Engineering

17. 17
Further developments
Further developments
• Aggregation dynamics:
– Particle nucleation
– Micellization
• Energy barriers:
– Phase transfer
– Phase transition
• Diffusion in polymer media
• Multiscale integration:
– Secondary particle nucleation
– Particle morphology
– Swelling equilibrium and dynamics
– …
 Outlook
Outlook

18. 18
Concluding remarks
Concluding remarks
• Emulsion polymerization is a complex multiscale
stochastic process.
• A consistent mechanism of emulsion polymerization
can only be formulated within this framework.
• The modeling, simulation and integration of the
different scales is a powerful tool for the investigation
and understanding of emulsion polymerization.
• Some of these results can be generalized to other
types of heterogeneous and homogeneous
polymerization processes.
 Outlook
Outlook