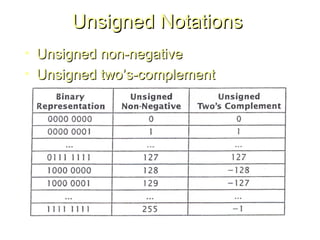
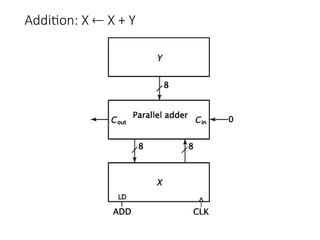
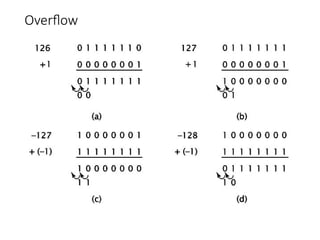
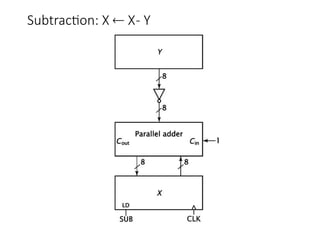
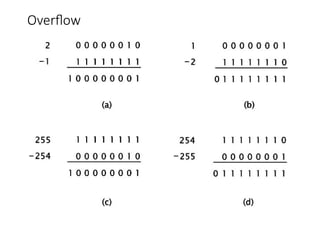
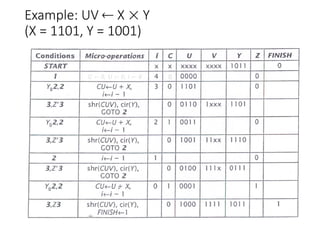
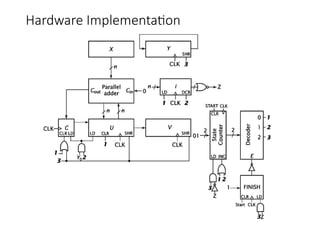
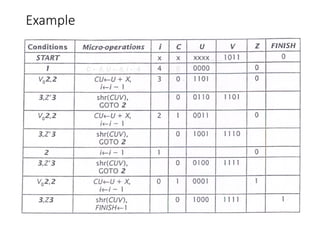
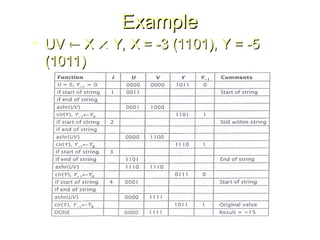
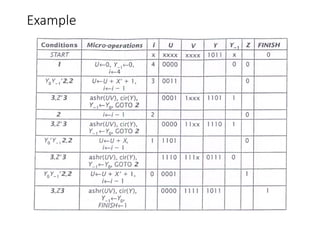
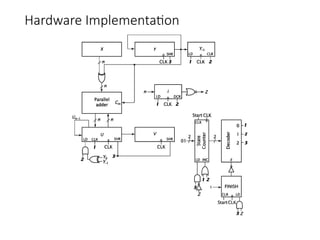
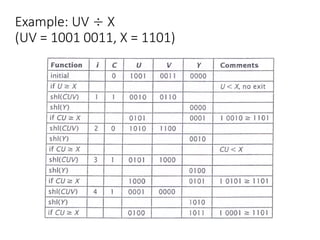
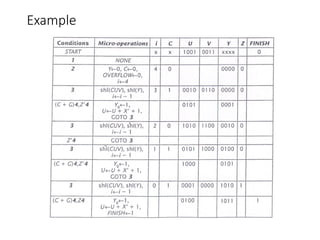
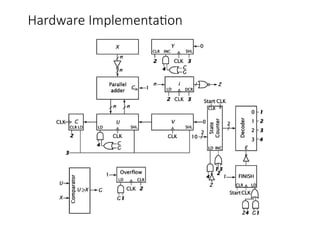
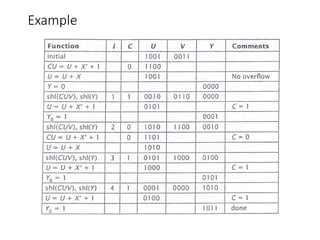
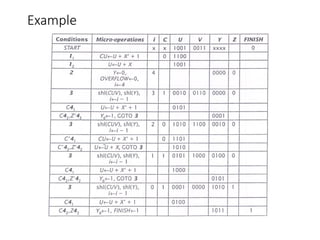
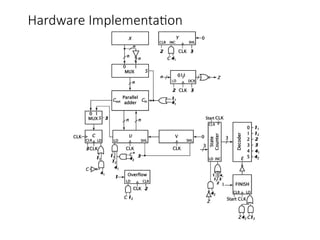
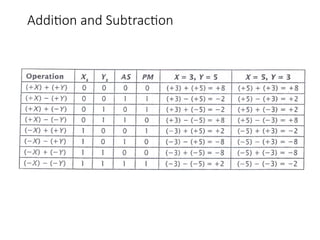
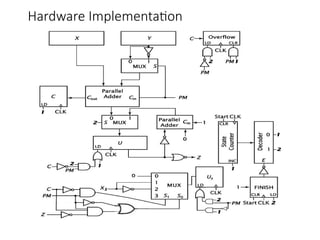
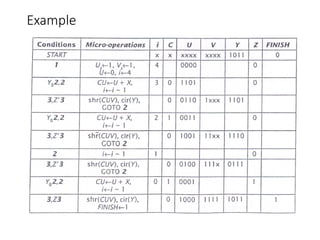
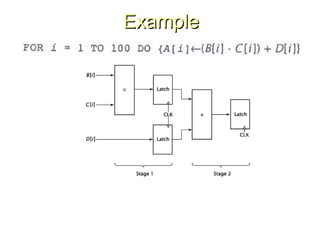
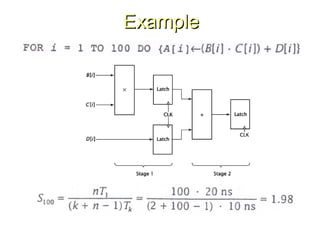
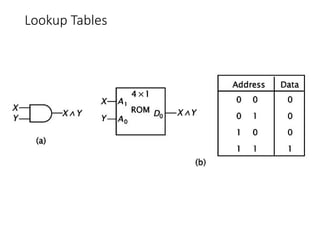
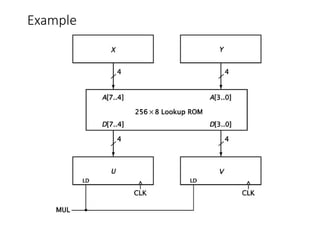
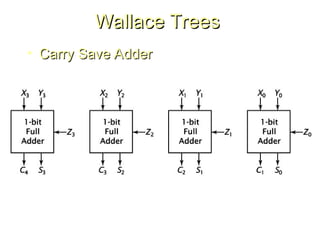
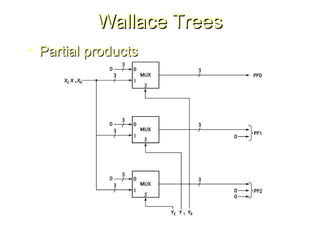
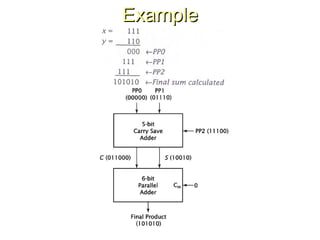
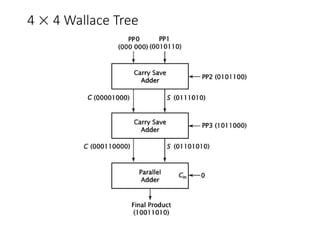
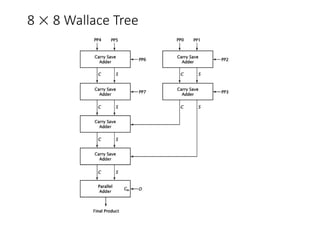
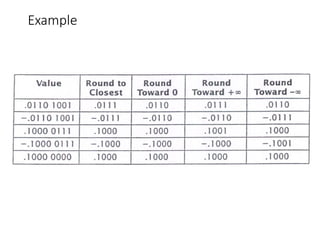
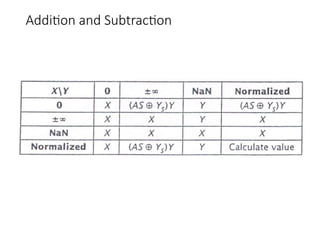
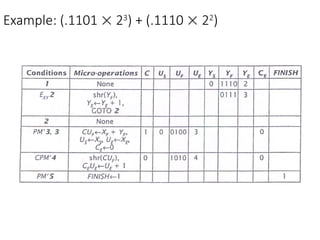
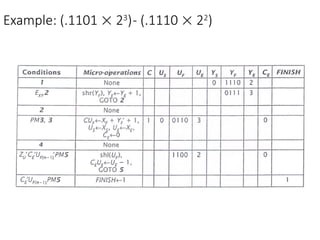
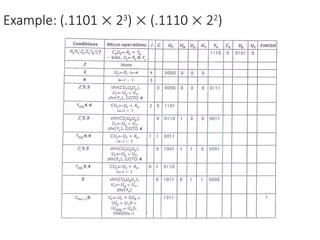
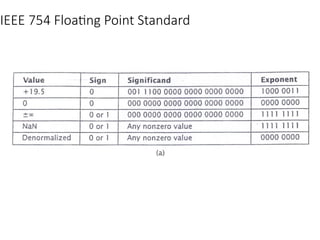
Chapter 8 discusses computer arithmetic, covering topics such as unsigned and signed notations, binary coded decimal, and specialized arithmetic hardware. It also addresses floating point numbers and the IEEE 754 standard, illustrating methods for multiplication, division, and the use of various notations. The chapter includes examples, code implementations, and optimizations related to these arithmetic processes.

1. Chapter 8
Computer Arithmetic

2. Chapter Outline
• Unsigned notations
• Signed notations
• Binary Coded Decimal
• Specialized arithmetic hardware
• Floating point numbers
• IEEE 754 floating point standard

3. Unsigned Notations
• Unsigned non-negative
• Unsigned two’s-complement

4. Unsigned Notations
Unsigned Notations
• Unsigned non-negative
Unsigned non-negative
• Unsigned two
Unsigned two’
’s-complement
s-complement

5. Addition: X  X + Y

6. Overflow

7. Subtraction: X  X- Y

8. Overflow

9. Multiplication
• A non-optimal method
z = 0
FOR i = 1 TO y DO { z = z + x }

10. Multiplication
• A more typical method

11. Multiplication
• Calculating running totals

12. Multiplication
• Shifting partial results to align sums

13. Shift-add Multiplication Algorithm
C = 0, U = 0;

14. Example: UV  X  Y
(X = 1101, Y = 1001)
C = 0, U = 0 0

15. RTL Code
C  0, U  0, i  n

16. Example: UV  X  Y
(X = 1101, Y = 1001)
C  0, U  0, i  4 0

17. Hardware Implementation

18. Optimizing the RTL Code
• UV  X  V
• Register Y not needed
• One operand is lost

19. Optimizing the RTL Code
C  0, U  0

20. Example
C  0, U  0, i  4 0

21. Booth’s Algorithm
• Multiplying unsigned 2’s-complement numbers

22. Example
• UV  X  Y, X = -3 (1101), Y = -5 (1011)

23. Example
Example
• UV
UV 
 X
X 
 Y, X = -3 (1101), Y = -5
Y, X = -3 (1101), Y = -5
(1011)
(1011)

24. RTL Code

25. Example

26. Optimized RTL Code

27. Hardware Implementation

28. Division
• A non-optimal method

29. Division
• A more typical method

30. Division
• Shifting results to align remainders

31. Shift-subtract Division Algorithm

32. Example: UV  X
(UV = 1001 0011, X = 1101)

33. RTL Code

34. Example

35. Hardware Implementation

36. Restoring Division Algorithm

37. Overflow Comparison

38. Example

39. RTL Code

40. Example

41. Hardware Implementation

42. Signed Notations
• Signed-magnitude

43. Signed Notations
Signed Notations
• Signed-magnitude
Signed-magnitude
• Signed-2
Signed-2’
’s complement
s complement

44. Signed Notations
Signed Notations
• Signed-magnitude
Signed-magnitude
• Signed-2
Signed-2’
’s complement
s complement
Value Signed-magnitude Signed-2
Value Signed-magnitude Signed-2’
’s complement
s complement
+3 0 0011 0 0011
+3 0 0011 0 0011
-3 1 0011 1 1101
-3 1 0011 1 1101

45. Addition and Subtraction

46. RTL Code

47. RTL Code
RTL Code

48. Examples

49. Examples

50. Examples

51. Hardware Implementation

52. Multiplication

53. Example

54. Binary Coded Decimal (BCD)
• Every 4 bits = 1 decimal digit
• 1 bit sign
• Example: +27 = 0 0010 0111

55. BCD Adder

56. Nine’s Complement
• Equivalent of 1’s complement in binary

57. Nine
Nine’
’s Complement
s Complement
• Equivalent of 1
Equivalent of 1’
’s complement in binary
s complement in binary

58. RTL Code

59. Examples

60. Examples

61. Examples

62. Hardware Implementation

63. Multiplication
• dshr: decimal shift right

64. Multiplication
Multiplication
• dshr: decimal shift right
dshr: decimal shift right

65. Example

66. Arithmetic Pipelines
• Increase throughput

67. Arithmetic Pipelines
Arithmetic Pipelines
• Increase throughput
Increase throughput
• Speedup:
Speedup:

68. Example

69. Example
Example

70. Example
Example

71. Steady State Speedup

72. Steady State Speedup
Steady State Speedup

73. Speedup with Latch Delays

74. Speedup with Latch Delays
Speedup with Latch Delays

75. Lookup Tables

76. Example

77. Wallace Trees
• Carry Save Adder

78. Wallace Trees
Wallace Trees
• Carry Save Adder
Carry Save Adder

79. Wallace Trees
• Partial products

80. Wallace Trees
Wallace Trees
• Partial products
Partial products

81. Example

82. Example
Example

83. 4  4 Wallace Tree

84. 8  8 Wallace Tree

85. Floating Point Numbers
• Sign, Significand, Exponent
• Normalized:
-1234.5678 = -.12345678  104
• NaN
• Biasing

86. Floating Point Numbers
• Precision
• Gap
• Range
• Round, Guard, Sticky bits

87. Rounding
• Round toward nearest
• Round toward 0
• Round toward +
• Round toward -

88. Example

89. Addition and Subtraction

90. Addition and Subtraction

91. RTL Code

92. Example: (.1101  23
) + (.1110  22
)

93. Example: (.1101  23
)- (.1110  22
)

94. Multiplication
• Check for special values
• Add exponents
• Multiply significands
• Normalize result

95. RTL Code

96. Example: (.1101  23
)  (.1110  22
)

97. IEEE 754 Floating Point Standard
• 1 significand < 2
• Single of double precision

98. IEEE 754 Floating Point Standard

99. IEEE 754 Floating Point Standard

100. Denormalized Values
• Used to express smaller numbers than possible with normalized
notation
• Smallest normalized value: 2-126
(single precision)
• Smallest denormalized value: 2-149
(single precision)

101. Summary
• Unsigned notations
• Signed notations
• Binary Coded Decimal
• Specialized arithmetic hardware
• Floating point numbers
• IEEE 754 floating point standard