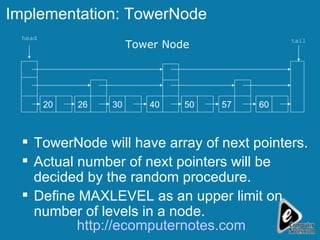
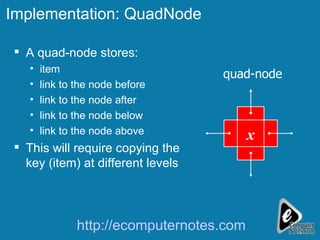
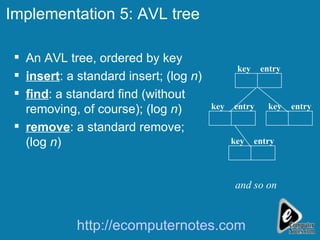
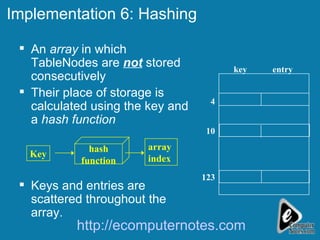
The document discusses various data structures including skip lists, AVL trees, and hashing techniques. It explains implementations such as tower nodes and quad nodes, and highlights the performance benefits of skip lists, noting their expected logarithmic time complexity for search, insertion, and deletion operations. Additionally, it covers hashing methods, emphasizing the importance of an efficient hash function and the use of prime numbers for table sizes to optimize data storage.

1. Class No.35 Data Structures http://ecomputernotes.com

2. Skip List: Implementation   S 0 S 1 S 2 S 3   45 12 23 34   34   23 34 http://ecomputernotes.com

3. Implementation: TowerNode TowerNode will have array of next pointers. Actual number of next pointers will be decided by the random procedure. Define MAXLEVEL as an upper limit on number of levels in a node. http://ecomputernotes.com 40 50 60 head tail 20 30 26 57 Tower Node

4. Implementation: QuadNode A quad-node stores: item link to the node before link to the node after link to the node below link to the node above This will require copying the key (item) at different levels x quad-node http://ecomputernotes.com

5. Skip Lists with Quad Nodes 56 64 78  31 34 44  12 23 26    31  64  31 34  23 S 0 S 1 S 2 S 3 http://ecomputernotes.com

6. Performance of Skip Lists In a skip list with n items The expected space used is proportional to n . The expected search, insertion and deletion time is proportional to log n . Skip lists are fast and simple to implement in practice http://ecomputernotes.com

7. Implementation 5: AVL tree An AVL tree, ordered by key insert : a standard insert; (log n ) find : a standard find (without removing, of course); (log n ) remove : a standard remove; (log n ) and so on http://ecomputernotes.com key entry key entry key entry key entry

8. Anything better? So far we have find, remove and insert where time varies between constant log n . It would be nice to have all three as constant time operations! http://ecomputernotes.com

9. An array in which TableNodes are not stored consecutively Their place of storage is calculated using the key and a hash function Keys and entries are scattered throughout the array. Implementation 6: Hashing key entry Key hash function array index 4 10 123 http://ecomputernotes.com

10. insert : calculate place of storage, insert TableNode; (1) find : calculate place of storage, retrieve entry; (1) remove : calculate place of storage, set it to null; (1) Hashing key entry 4 10 123 All are constant time (1) ! http://ecomputernotes.com

11. Hashing We use an array of some fixed size T to hold the data. T is typically prime. Each key is mapped into some number in the range 0 to T-1 using a hash function , which ideally should be efficient to compute. http://ecomputernotes.com

12. Example: fruits Suppose our hash function gave us the following values: hashCode("apple") = 5 hashCode("watermelon") = 3 hashCode("grapes") = 8 hashCode("cantaloupe") = 7 hashCode("kiwi") = 0 hashCode("strawberry") = 9 hashCode("mango") = 6 hashCode("banana") = 2 http://ecomputernotes.com kiwi banana watermelon apple mango cantaloupe grapes strawberry 0 1 2 3 4 5 6 7 8 9

13. Example Store data in a table array: table[5] = "apple" table[3] = "watermelon" table[8] = "grapes" table[7] = "cantaloupe" table[0] = "kiwi" table[9] = "strawberry" table[6] = "mango" table[2] = "banana" http://ecomputernotes.com kiwi banana watermelon apple mango cantaloupe grapes strawberry 0 1 2 3 4 5 6 7 8 9

14. Example Associative array: table["apple"] table["watermelon"] table["grapes"] table["cantaloupe"] table["kiwi"] table["strawberry"] table["mango"] table["banana"] http://ecomputernotes.com kiwi banana watermelon apple mango cantaloupe grapes strawberry 0 1 2 3 4 5 6 7 8 9

15. Example Hash Functions If the keys are strings the hash function is some function of the characters in the strings. One possibility is to simply add the ASCII values of the characters: TableSize ABC h Example TableSize i str str h length i )% 67 66 65 ( ) ( : % ] [ ) ( 1 0                http://ecomputernotes.com

16. Finding the hash function int hashCode( char* s ) { int i, sum; sum = 0; for(i=0; i < strlen(s); i++ ) sum = sum + s[i]; // ascii value return sum % TABLESIZE; } http://ecomputernotes.com

17. Example Hash Functions Another possibility is to convert the string into some number in some arbitrary base b ( b also might be a prime number): T b b b ABC h Example T b i str str h length i i )% 67 66 65 ( ) ( : % ] [ ) ( 2 1 0 1 0                 http://ecomputernotes.com

18. Example Hash Functions If the keys are integers then key%T is generally a good hash function, unless the data has some undesirable features. For example, if T = 10 and all keys end in zeros, then key%T = 0 for all keys. In general, to avoid situations like this, T should be a prime number. http://ecomputernotes.com