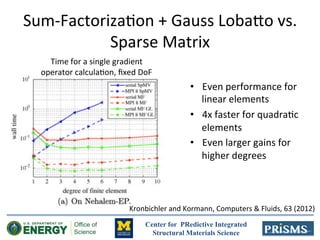
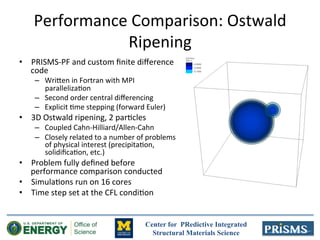
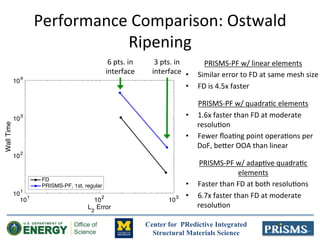
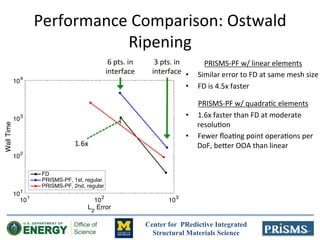
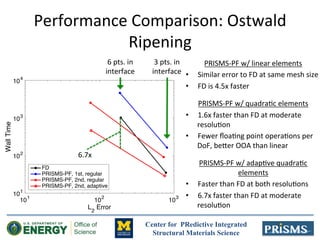
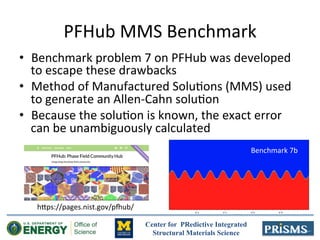
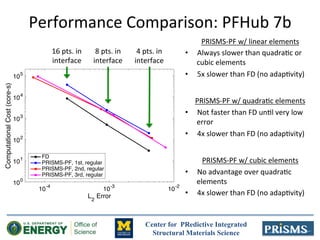
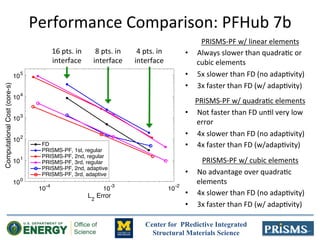
The document discusses the development of 'prisms-pf', an open-source phase field modeling framework aimed at enhancing computational performance through sum-factorization and Gauss-Lobatto quadrature methods. It compares the framework's performance against traditional finite difference methods, highlighting its potential for faster calculations in complex simulations like Ostwald ripening. Additionally, it notes the computational resources and support from various institutions underpinning this research.