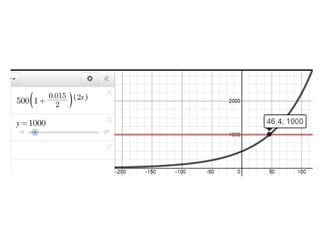
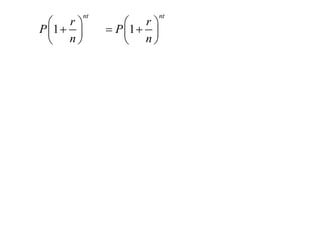Sheldon deposits $500 into a bank account paying annual interest of 1.5%. The document shows the calculation to determine how long it will take for the initial deposit to double to $1000 using the compound interest formula. An equation is set up and solved to find that it will take approximately 5 years for Sheldon's money to double.

1. Sheldon deposits $500 at Big Bang Bank in an
account that pays 1.5% compounded annually.
How long will it take for Sheldon to double his
money?

2. 500(1 0.015) 1000x
 
Write an equation and solve.
Year Value
0 500
1
2
3
x
Sheldon deposits $500 into a bank account that
pays 1.5% compounded annually. How long will
it take for Sheldon to double his money?
500(1 0.015)
2
500(1 0.015)
3
500(1 0.015)
500(1 0.015)x


5. In general
•deposit P dollars
(called the PRINCIPLE)
• in an account that pays r percentage
(called the annual percentage rate, or the APR,
and is expressed as a decimal)
•that compounds ONCE annually
• then the amount A
•after t years
•can be found by the formula
(1 )t
PA r 

6. However, interest can be compounded
more frequently than once per year.
This leads to a modified formula.

7. Brady invests $500 at Patriots Bank. The
account has an APR of 1.5% that
compounds twice a year. How long will it
take for the principle to double?

8. Brady invests $500 at Patriots Bank. The
account has an APR of 1.5% that
compounds twice a year. How long will it
take for the principle to double?
Write an equation and solve.
Before we create a table, notice the APR
is 1.5%. But the account compounds
twice per year, so the APR must be
divided by 2.

9. Year Value
0 500
0.5
1
1.5
x
Principle
$500
APR
1.5%
Compounding
periods per year
2
0.01
2
1500
5 
 
 
2
0.015
0 15 0
2
 
 
 
3
0.015
0 15 0
2
 
 
 
2
0.015
0 15 0
2
x
 
 
 

12. In general:
•deposit P dollars
(called the PRINCIPLE)
• in an account that pays r percentage
(called the annual percentage rate, or the APR,
and is expressed as a decimal)
•that compounds n times annually
• then the amount A
•after t years
•can be found by the formula
1
tn
A P
r
n
 
  
 

13. 1
nt
r
P
n
 
 
 
1
nt
r
P
n
 
  
 