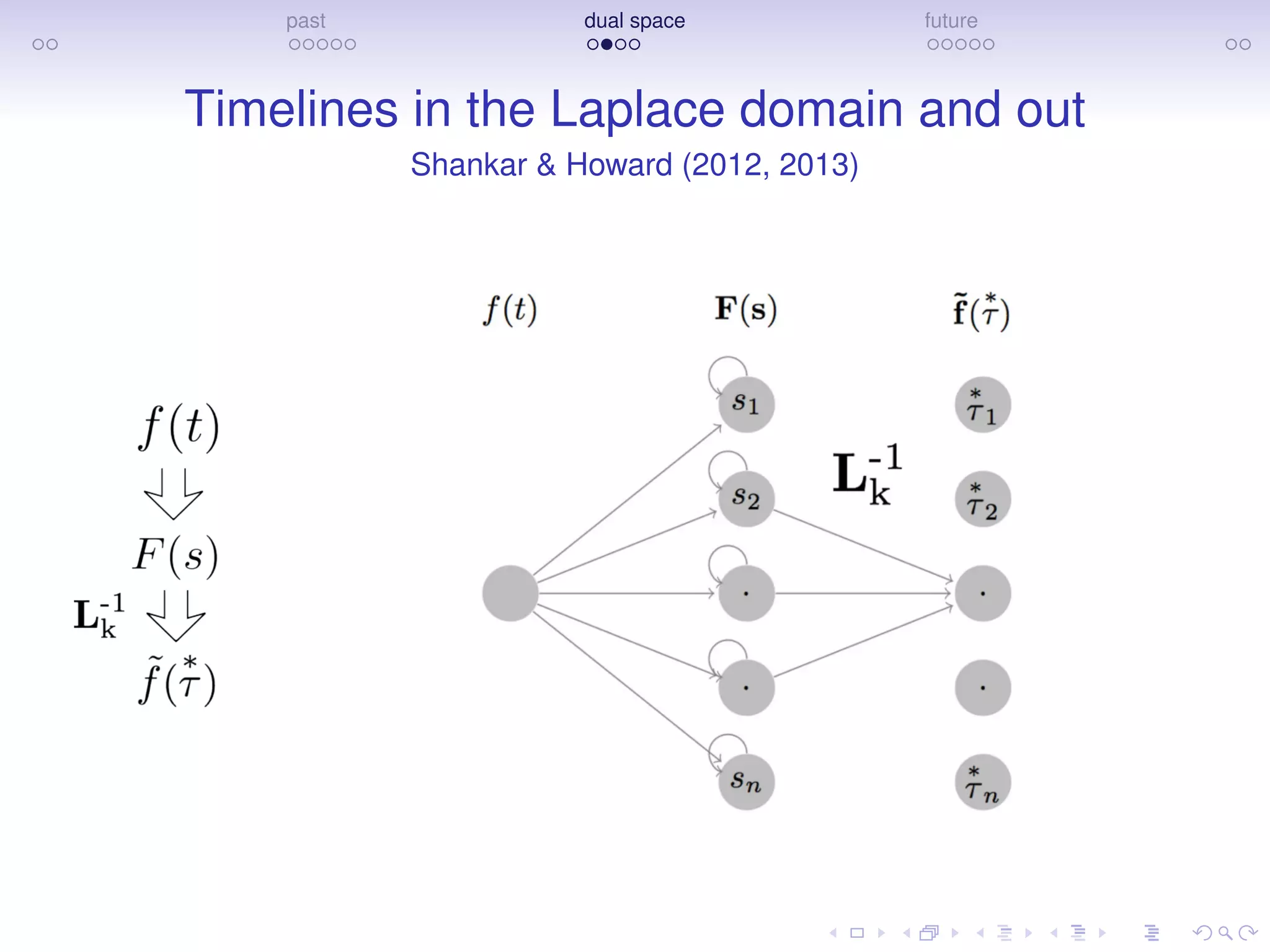
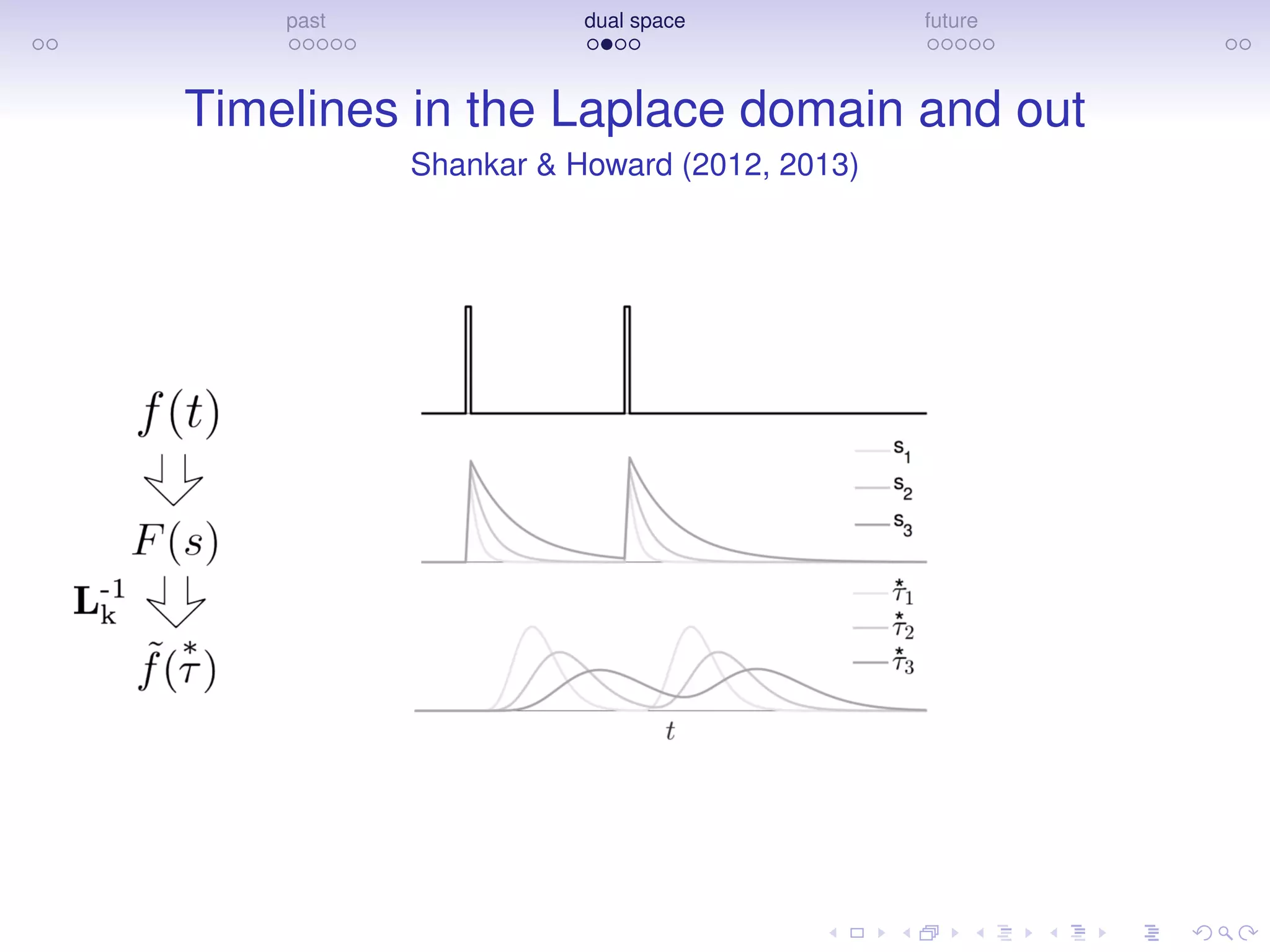
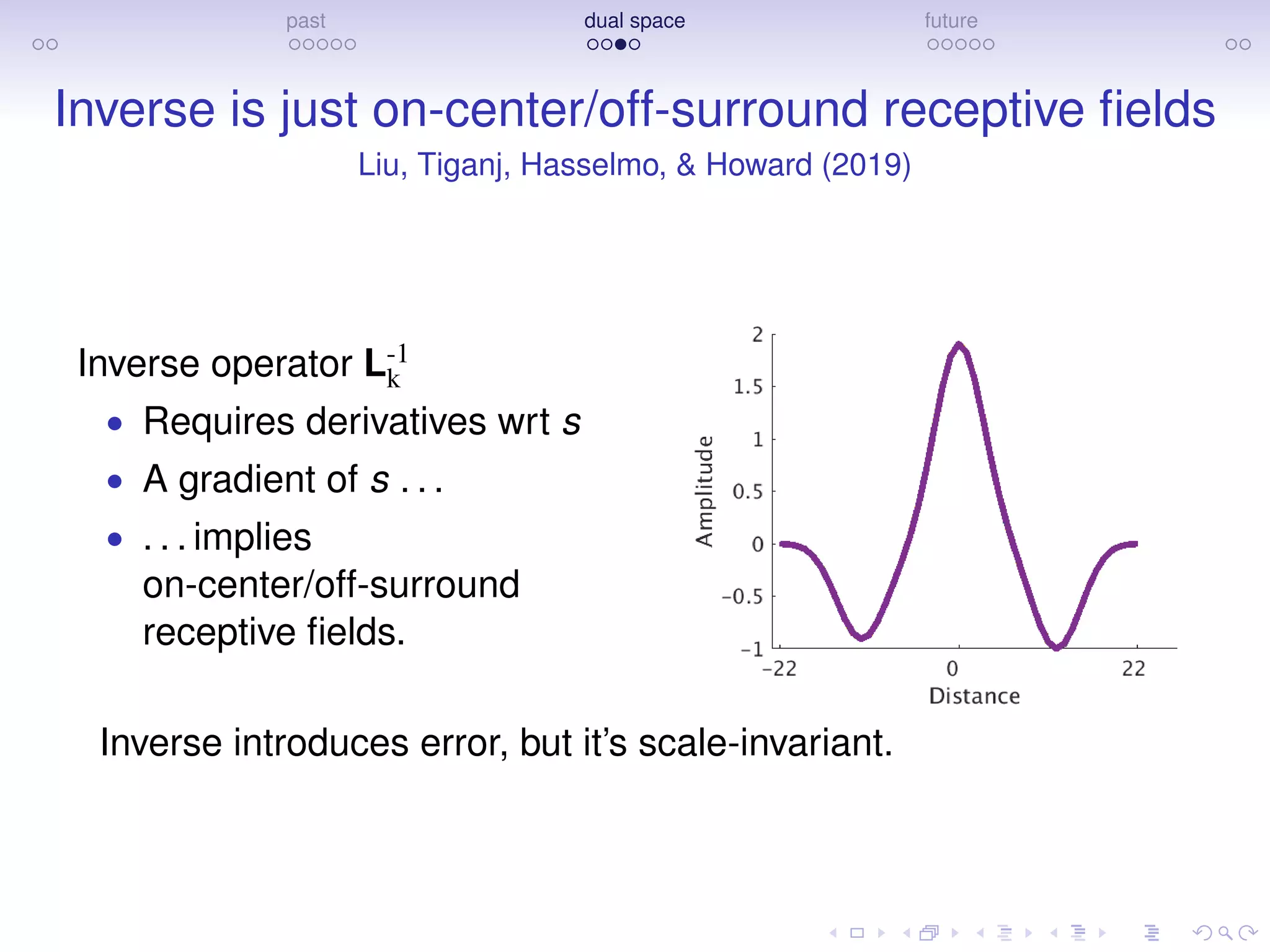
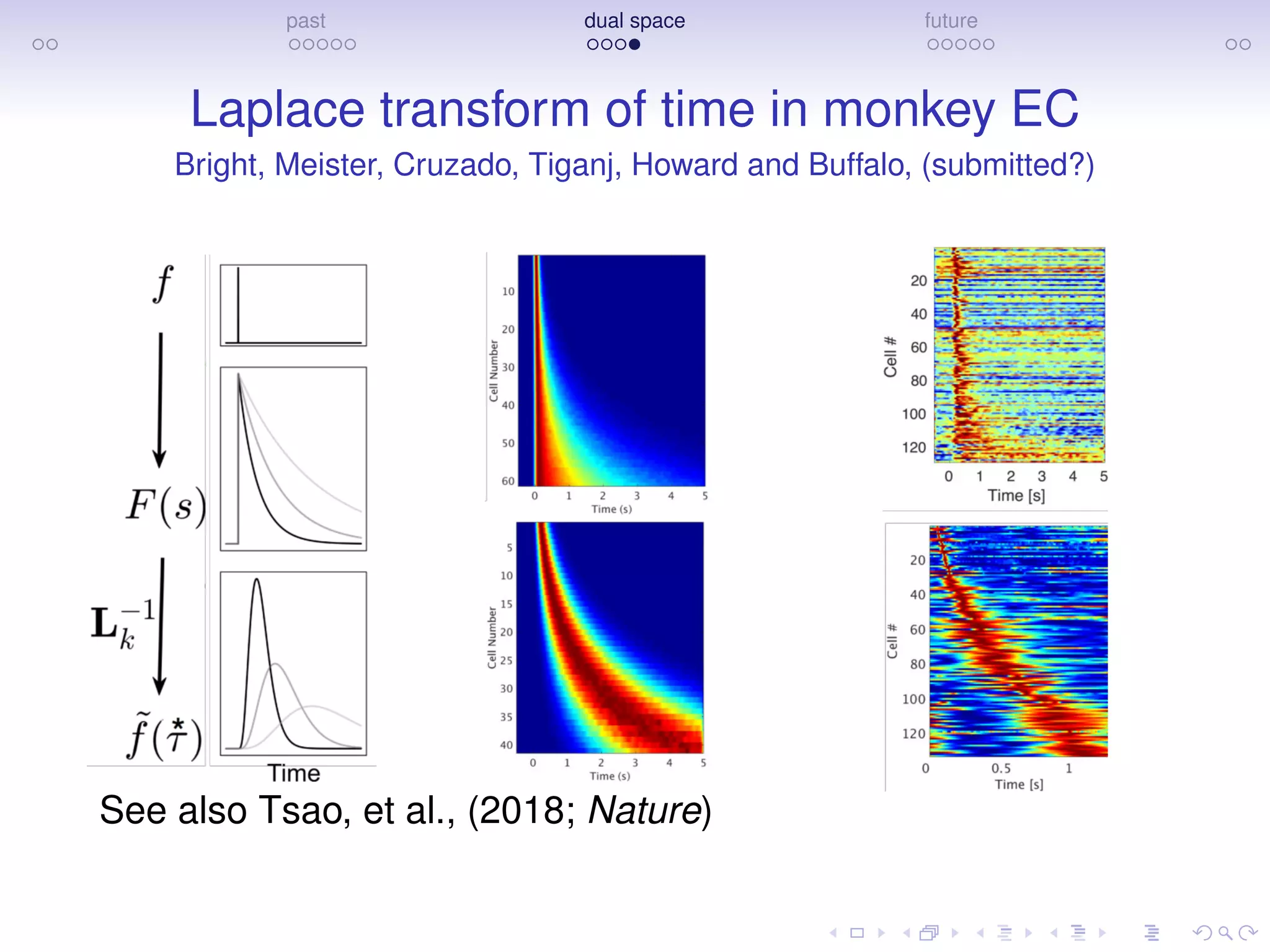
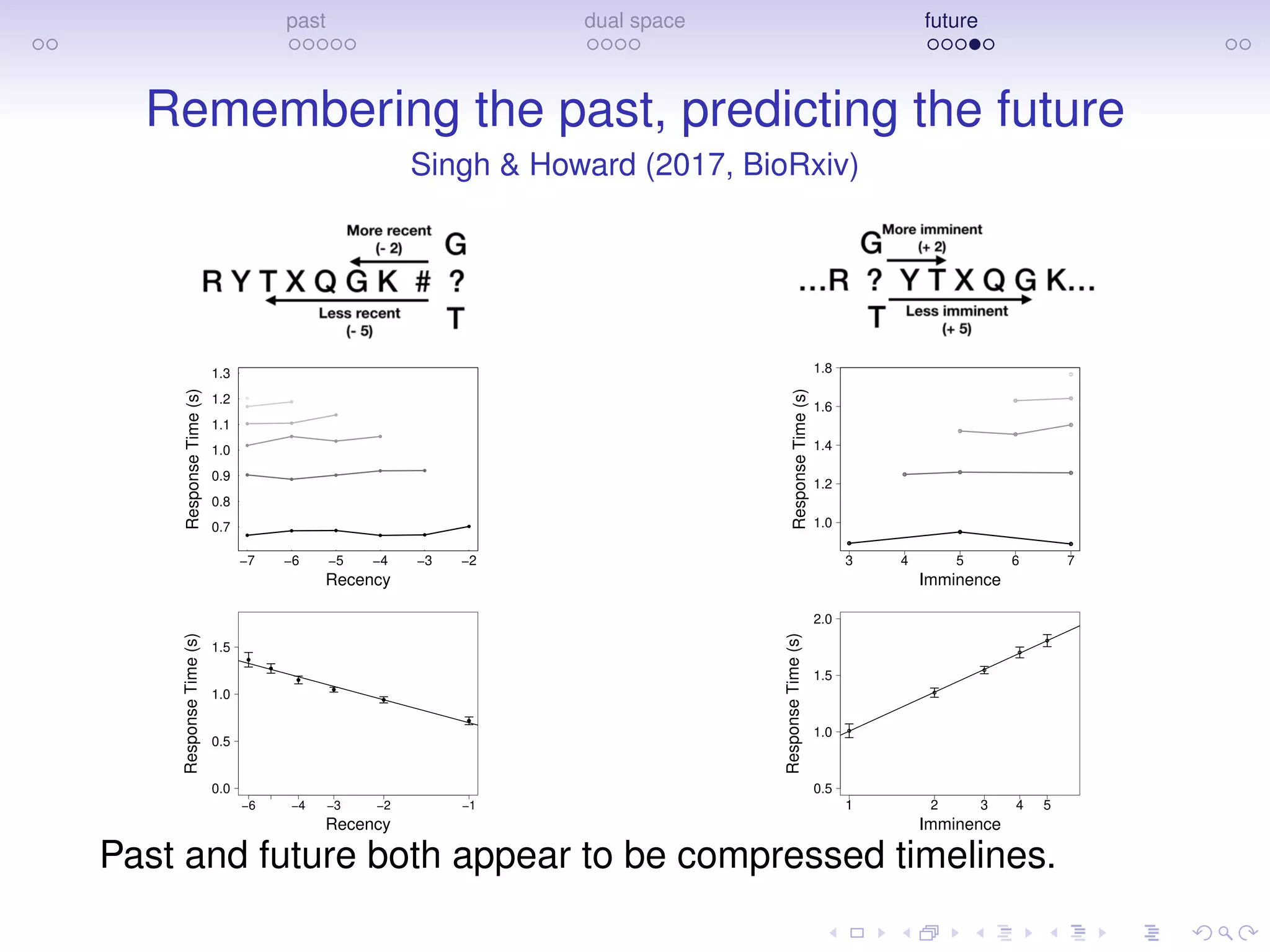
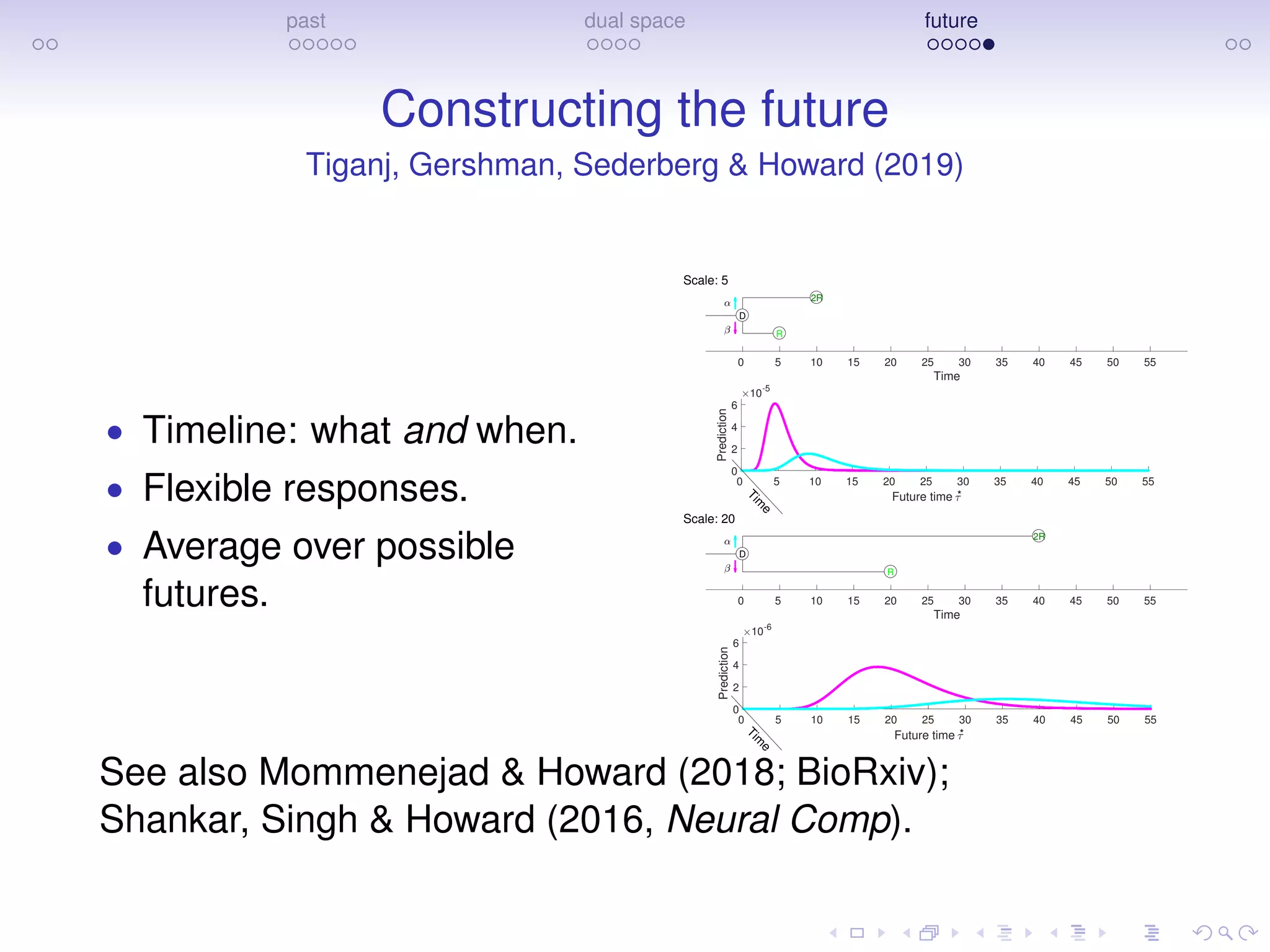
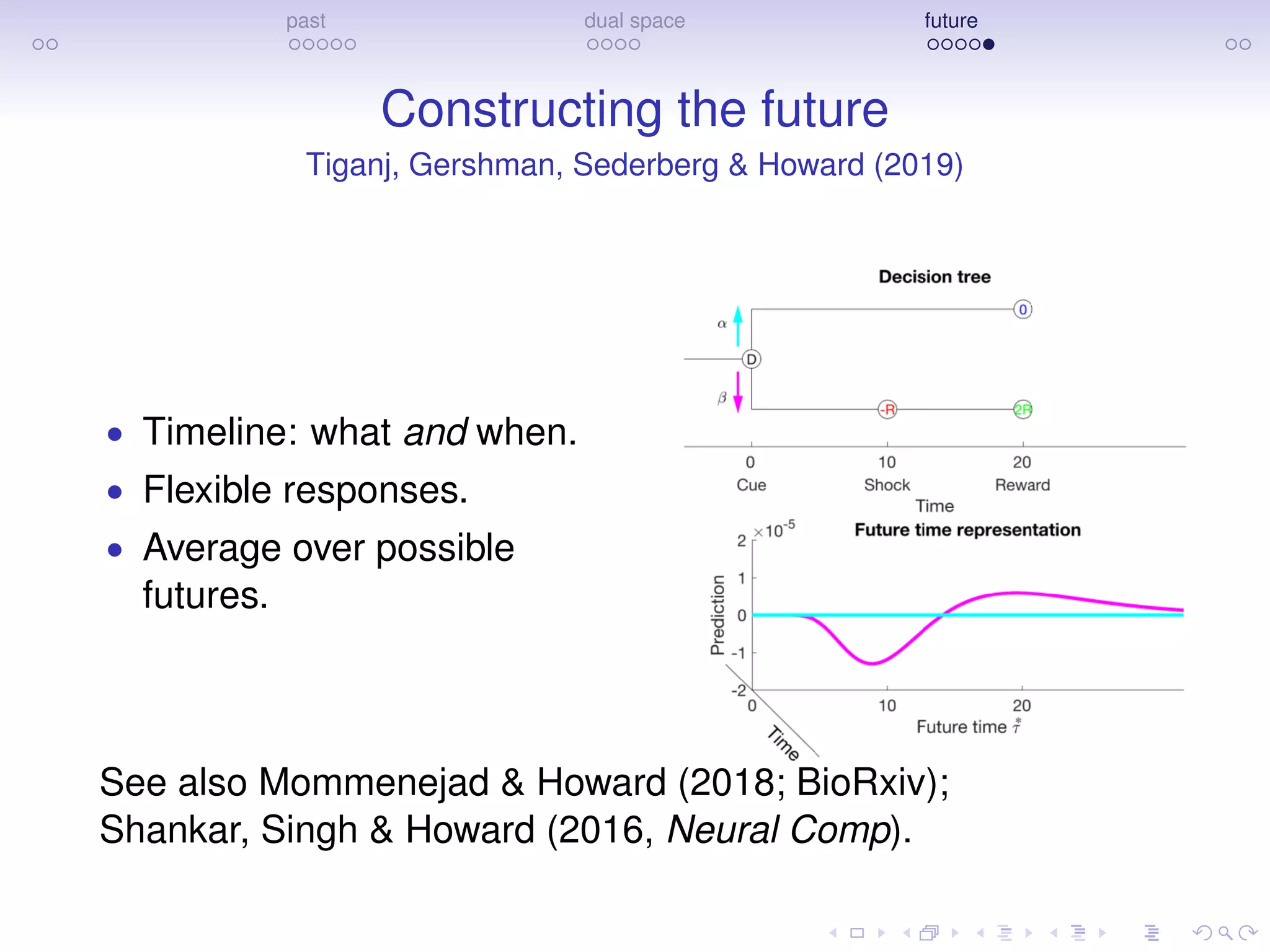
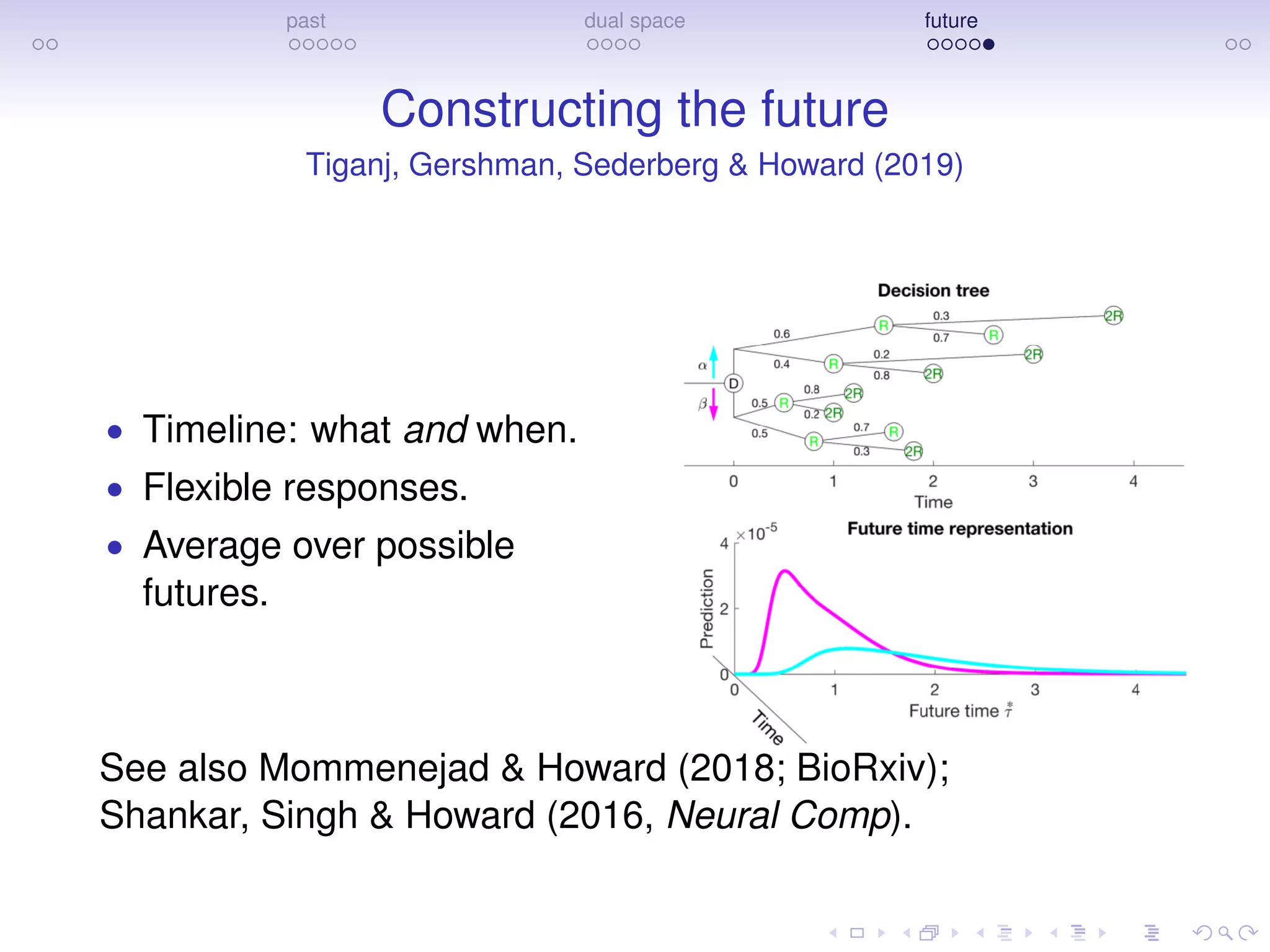
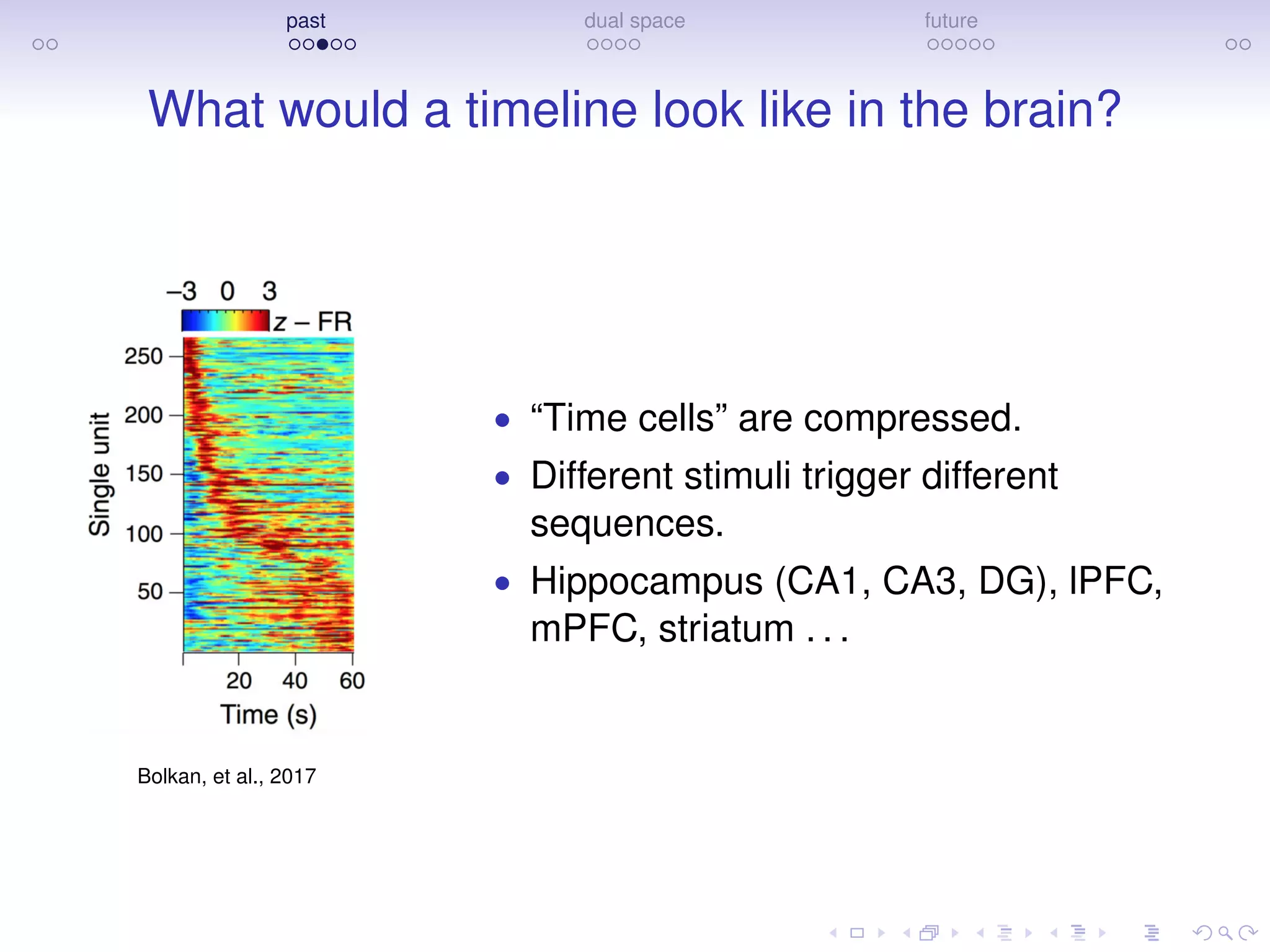
The document discusses research on how the brain represents the past and the future, emphasizing a dual space model based on Laplace transforms. It presents evidence that memories of the past are compressed on a temporal axis and suggests similar mechanisms for predicting future events. The findings involve collaborative efforts from various researchers and are supported by funding from NIH, NSF, and private sector sources.







![past dual space future
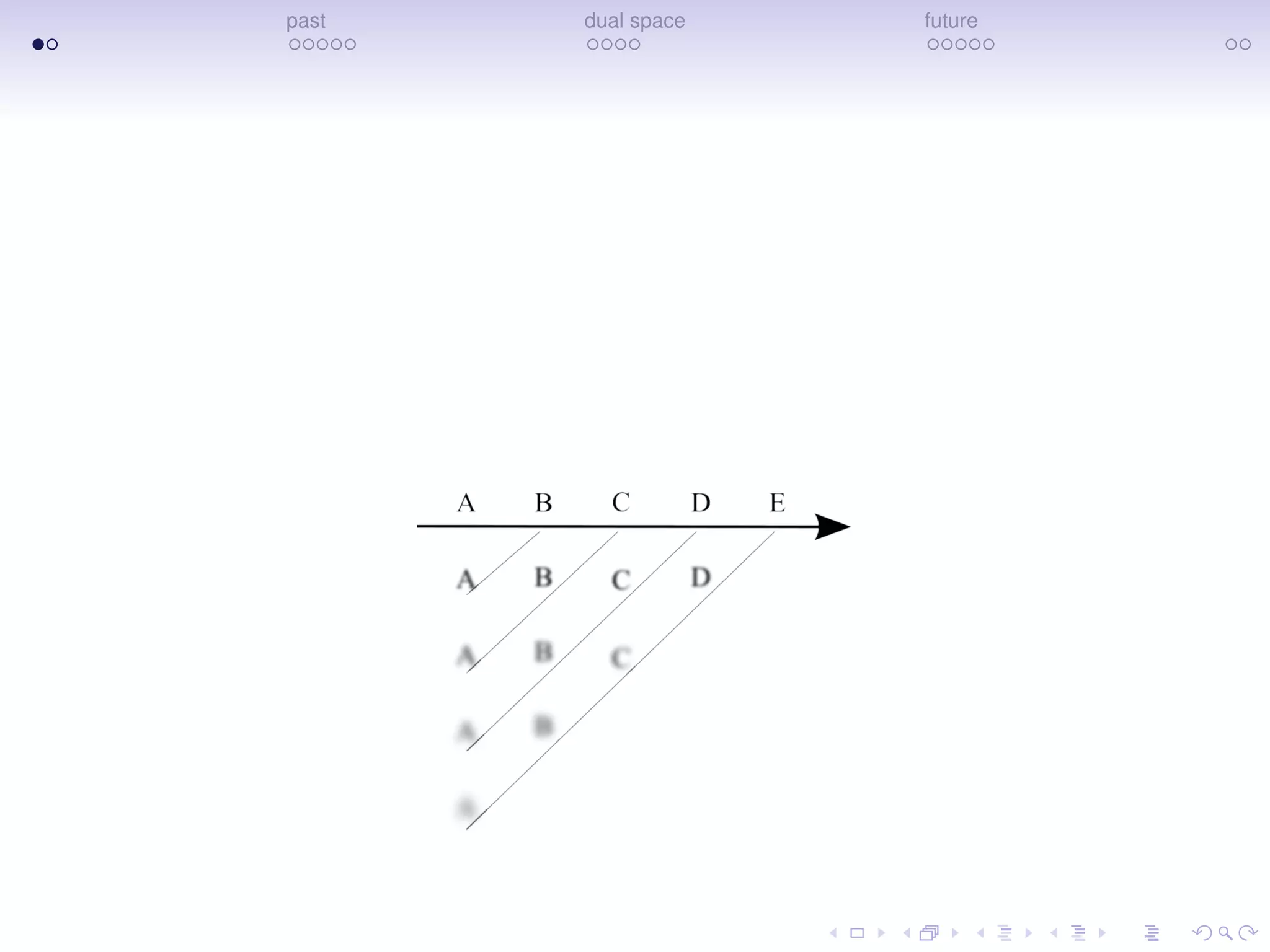
Compressed record of what happened when
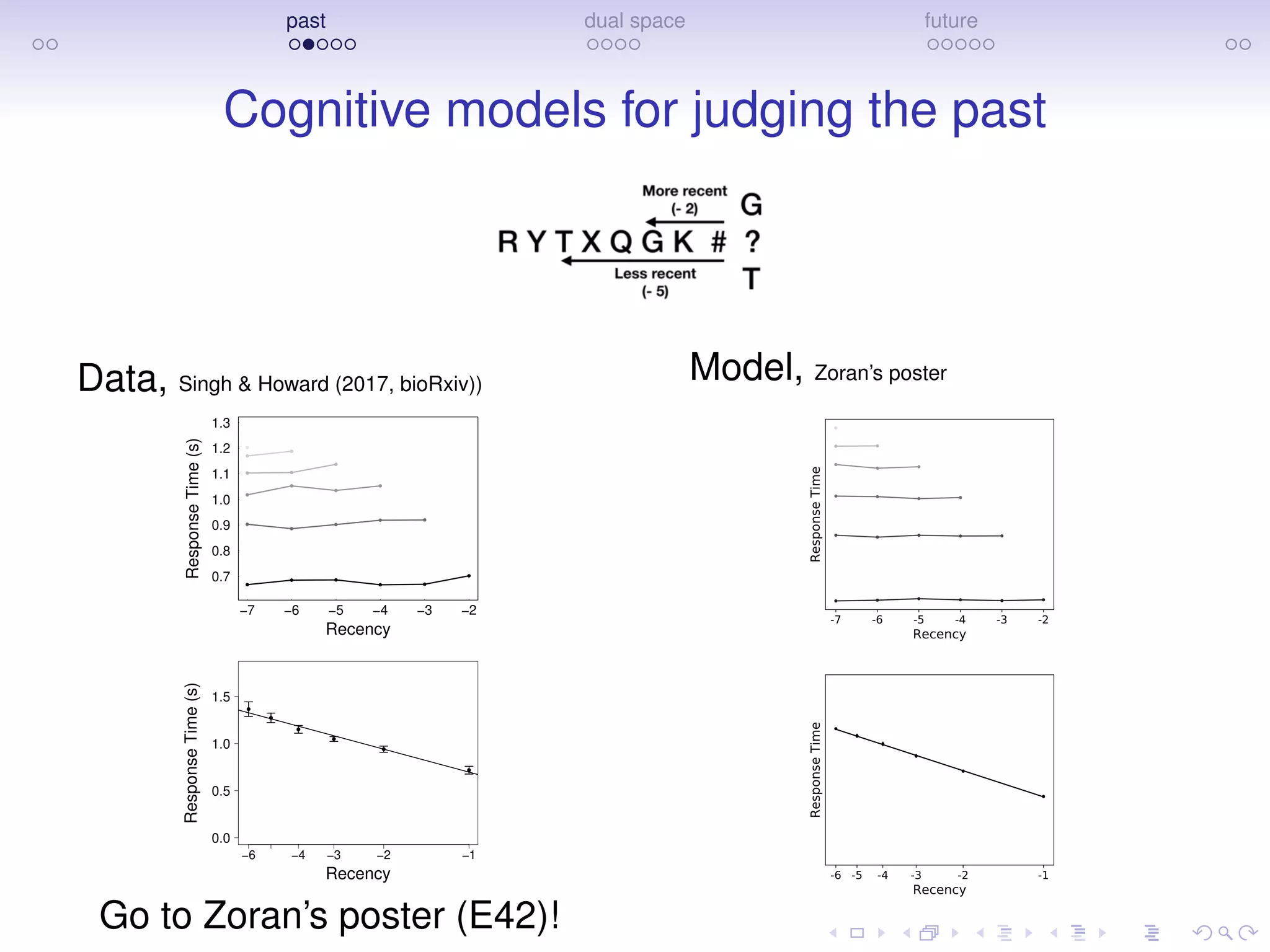
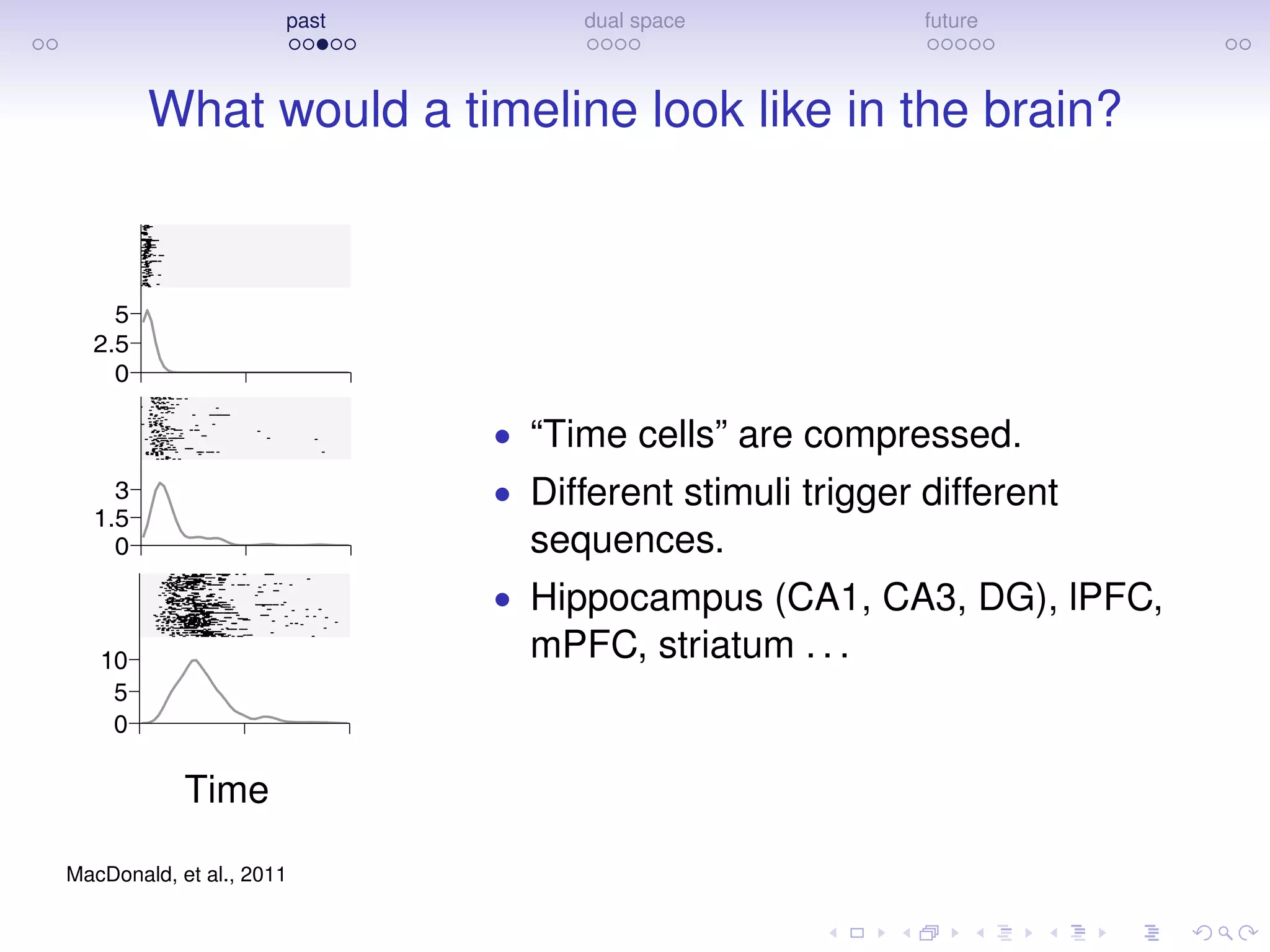
Tiganj, Cromer, Roy, Miller, & Howard (2018, J Cog Neuro)
Monkey WM task; remember different stimuli during delay
Dog Cat Car/Truck
0 0.5 1 1.5
Time [s]
50
100
150
200
Cell#
0 0.5 1 1.5
Time [s]
50
100
150
200
Cell#
0 0.5 1 1.5
Time [s]
50
100
150
200
Cell#](https://image.slidesharecdn.com/cognsci19-mwh-compressed-190330082801/75/CNS-2019-Mental-Models-of-Time-Marc-Howard-13-2048.jpg)