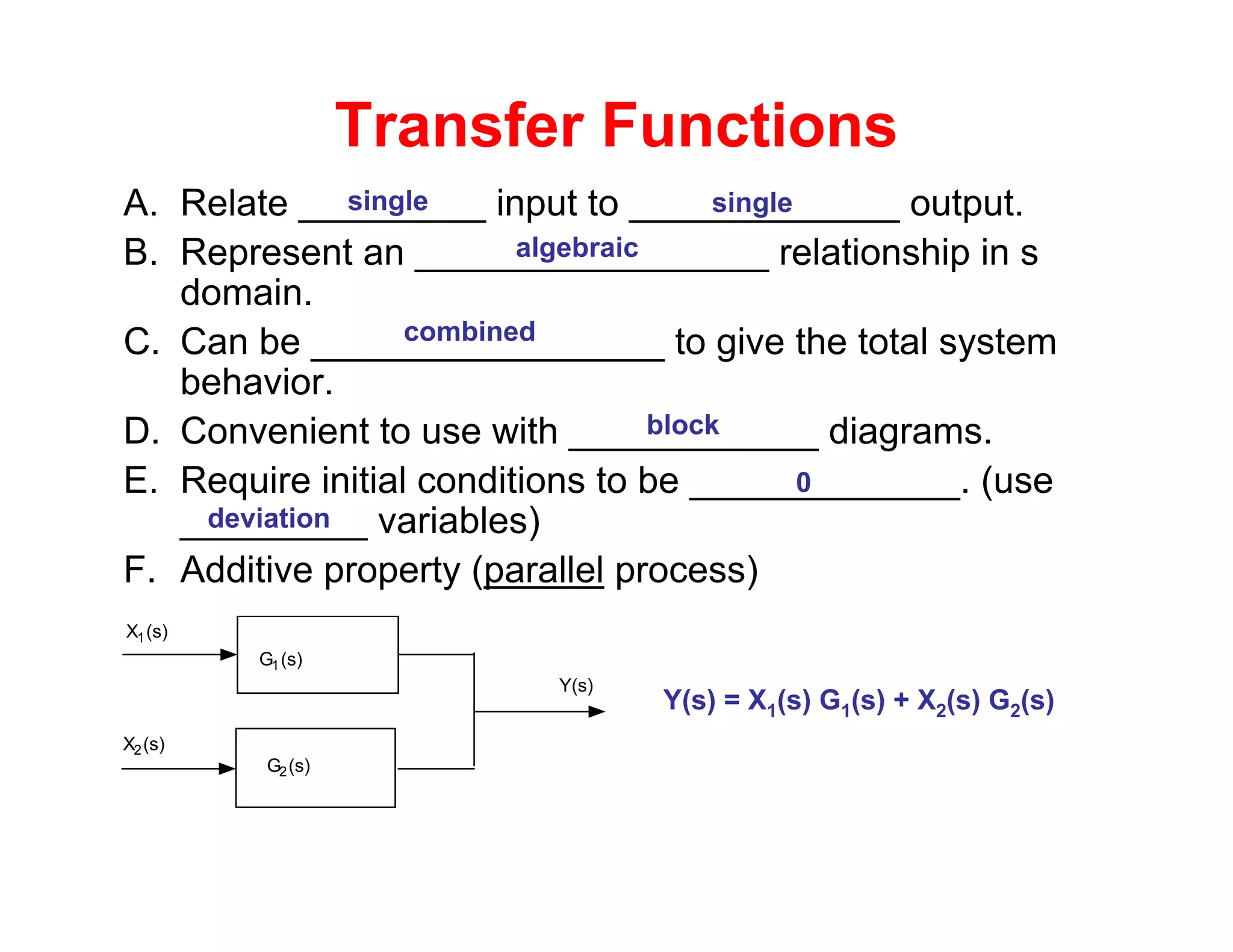
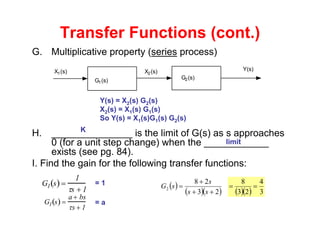
Transfer functions relate an input to an output in the s-domain and can represent systems. They have properties that allow them to be combined to model overall system behavior. Initial conditions must be specified when using transfer functions. The limit of a transfer function as s approaches 0 gives the steady state gain of the system. Group activities involved deriving and manipulating transfer functions to model capacitance, voltage, temperature, and heat transfer in systems.

1. Transfer Functions
A. Relate _________ input to _____________ output.
B. Represent an _________________ relationship in s
domain.
C. Can be _________________ to give the total system
behavior.
D. Convenient to use with ____________ diagrams.
E. Require initial conditions to be _____________. (use
_________ variables)
F. Additive property (parallel process)
single single
algebraic
combined
block
0
deviation
G1(s)
G2(s)
X2(s)
X1(s)
Y(s)
Y(s) = X1(s) G1(s) + X2(s) G2(s)

2. Transfer Functions (cont.)
G. Multiplicative property (series process)
H. _______________ is the limit of G(s) as s approaches
0 (for a unit step change) when the ____________
exists (see pg. 84).
I. Find the gain for the following transfer functions:
G2(s)
X2(s)
G1(s)
X1(s) Y(s)
Y(s) = X2(s) G2(s)
X2(s) = X1(s) G1(s)
So Y(s) = X1(s)G1(s) G2(s)
K
limit
G1 s
( ) =
1
τs + 1
G1 s
( ) =
a + bs
τs + 1
( )
( )( )
2
3
2
8
2
+
+
+
=
s
s
s
s
G
= 1
= a
( )( ) 3
4
2
3
8
=
=

3. Group Activity
1. Find ′
C (s) / ′
Ci(s)
)
(
)
(
)
( s
C
V
q
s
C
V
q
s
C
s i
′
−
′
=
′
)
(
)
( s
C
V
q
s
C
V
q
s i
′
=
′
⎟
⎠
⎞
⎜
⎝
⎛
+
)
(
)
(
1 s
C
s
C
s
q
V
i
′
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
+
=
′
′
1
1
)
(
)
(
s
q
V
s
C
s
C
i
q
V
p =
τ
1
=
p
K
C
V
q
C
V
q
dt
C
d
i
′
−
′
=
′

4. Group Activity
2. Find ′
C (s) / ′
Ci(s)
)
(
1
)
(
)
( s
C
s
C
V
q
s
C
s i
′
−
′
=
′
β
( ) )
(
)
(
1 s
C
V
q
s
C
s i
′
=
′
+ β
β
( )
1
)
(
)
(
+
=
′
′
s
V
q
s
C
s
C
i β
β β
τ =
p
V
q
Kp β
=
C
C
k
V
q
C
V
q
dt
C
d
i
′
⎟
⎠
⎞
⎜
⎝
⎛
+
−
′
=
′
2
2
1/β

5. Group Activity
3. Find and
′
T (s)/ ′
Ti (s) ′
T (s)/ ′
Q (s)
d ′
T
dt
=
q
V
( ′
Ti − ′
T ) +
′
Q
ρVCp V
q
=
β
p
VC
ρ
α
1
=
Q
T
T
dt
T
d
i
′
+
′
−
′
=
′
α
β )
(
( ) ( ) ( ) ( )
s
Q
s
T
s
T
s
T
s i
′
+
′
−
′
=
′ α
β
β
( ) ( ) ( ) ( )
s
Q
s
T
s
T
s i
′
+
′
=
′
+ α
β
β
( ) ( ) ( )
s
Q
s
T
s
T
s i
′
+
′
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
β
α
β
1
1
( )
( )
⎟
⎠
⎞
⎜
⎝
⎛
+
=
′
′
1
1
1
s
s
T
s
T
i
β
( )
( )
⎟
⎠
⎞
⎜
⎝
⎛
+
=
′
′
1
1
s
s
Q
s
T
β
β
α