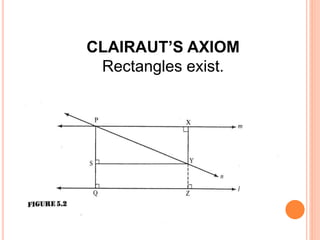
Alexis Claude Clairaut was a leading French geometer in the 18th century. Like others before him, he did not try to prove the parallel postulate but instead replaced it with his own axiom in his 1741 text. Clairaut's axiom stated that rectangles exist. He was able to prove that if rectangles exist, then the existence of triangles with angle sums of 180 degrees and convex quadrilaterals with angle sums of 360 degrees follows. This allows one to conclude that lines intersect, replacing the parallel postulate.

1. CLAIRAUT HISTORY
OF THE PARALLEL
POSTULATE

2. He was a leading French geometer. Like Wallis, he did
not try to prove the parallel postulate in neutral geometry
but replaced it in his 1741 text Eléments de géometrie
with another axiom.
Alexis Claude Clairaut
(1713-1765)

3. CLAIRAUT’S AXIOM
Rectangles exist.

4. Proof:
If we assume the latter, then the existence of rectangles follows
easily from Proposition 4.11 and Theorem 4.7. Conversely,
assume Clairaut’s axiom. Then by Theorem 4.7, all triangles have
angle sum 180°. And by introducing a diagonal, all convex
quadrilaterals have angle sum 360°. Return to Proclus’ argument
as illustrated in Figure 5.2. Let S be the foot of the perpendicular
from Y to segment PQ. S is on the same side of m as Y and Q
because segment SY is parallel to m (Corollary 1 to Theorem
4.1). Moreover, rectangle PXYS, which has three right angles, is
now known to be a rectangle. You can easily prove (Exercise 4)
that opposite sides of a rectangle are congruent, so PS = XY. By
Aristotle’s axiom (Chapter 3), Y can be chosen on the given ray of
n so that XY>PO. Then PS>PQ and P*Q*S. As above, Y is on the
same side of/as S, hence on the opposite side of/ from P.
Therefore/meets at some point between P and Y.

5. Thank You!