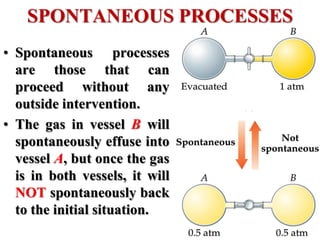
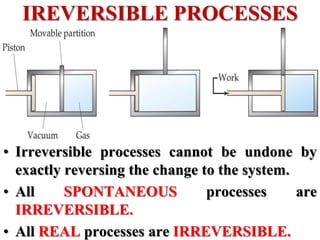
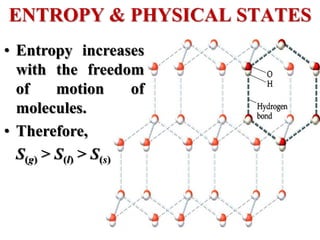
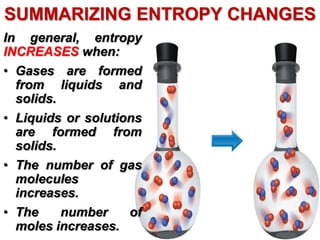
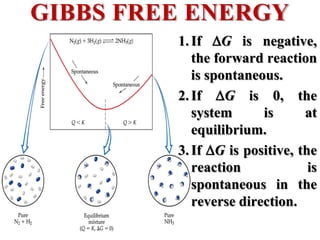
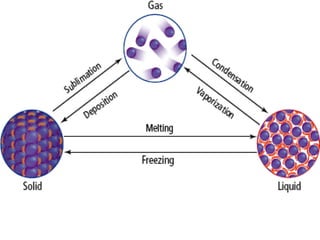
This document discusses key concepts from the first, second, and third laws of thermodynamics. It begins by defining spontaneous and reversible processes, explaining that spontaneous processes have a natural direction while reversible processes can return a system to its initial state. It then introduces entropy, describing how it increases for spontaneous processes based on the second law of thermodynamics. The document also discusses entropy at the molecular level and how it relates to temperature, phase changes, and the number of possible microscopic arrangements. Finally, it covers how entropy is used to define free energy and how free energy changes can indicate whether a process is spontaneous.

1. Dr. Pedro Villegas
pjva00@hotmail.com

2. OBJECTIVES
• To become familiar with Chemical
Thermodynamics concepts;
• To familiarize with Second and Third Law
of Thermodynamics;
• To understand Entropy and Free Energy
terms.
Brown, Lemay & Bursten, Chemistry:
The Central Science, 10th Ed. (Chapter 19)
TEXTBOOK

3. FIRST LAW OF THERMODYNAMICS
Lets recall from Chapter 5
1.Energy cannot be created nor
destroyed.
2.Therefore, the total energy of the
universe is a constant.
3.Energy can, however, be converted
from one form to another or
transferred from a system to the
surroundings or vice versa.
∆E= Ef – Ei ∆E= q + w

5. SPONTANEOUS PROCESSES
• Spontaneous processes
are those that can
proceed without any
outside intervention.
• The gas in vessel B will
spontaneously effuse into
vessel A, but once the gas
is in both vessels, it will
NOT spontaneously back
to the initial situation.

6. Processes that are
spontaneous in
one direction are
non-spontaneous
in the reverse
direction.
SPONTANEOUS PROCESSES

7. • Processes that are spontaneous at one
temperature may be non-spontaneous at other
temperatures.
• Above 0C it is spontaneous for ice to melt.
• Below 0C the reverse process is spontaneous.
SPONTANEOUS PROCESSES

8. REVERSIBLE PROCESSES
• In a reversible process
the system changes in
such a way that the
system and
surroundings can be put
back in their original
states by exactly
reversing the process.
• Changes are
infinitesimally SMALL
in a reversible process.

9. • Irreversible processes cannot be undone by
exactly reversing the change to the system.
• All SPONTANEOUS processes are
IRREVERSIBLE.
• All REAL processes are IRREVERSIBLE.
IREVERSIBLE PROCESSES

10. SUMMARIZING
• Spontaneous processes: Most chemical
reactions have a natural direction in
which they flow. In one direction they
are spontaneous, while in the other,
they are not.
• Reversible processes: the original state
of the system and surroundings can be
restored by reversing the change.
• Irreversible processes: the system
cannot return to its original state by
reversing the change.

11. ENTROPY
• Entropy (S) is a term coined by
Rudolph Clausius in the 19th Century.
• Clausius was convinced of the
significance of the ratio of heat
delivered and the temperature at which
it is delivered: q
T

12. Rudolf Julius Emanuel
Clausius (1822–1888),
was a German
Physicist, considered
one of the central
founders of the science
of Thermodynamics.
He introduced in 1865
the concept of Entropy.

13. • Entropy can be thought of as a
measure of the randomness of a system.
• It is related to the various modes of
motion in molecules.
• Like Internal Energy (E) and Enthalpy
(H) Entropy (S) is a state function.
• Therefore: S = Sfinal  Sinitial
ENTROPY

14. • For a process occurring at constant
temperature (an isothermal process):
• qrev = The heat that is transferred when
the process is carried out
REVERSIBLY at a constant
temperature.
• T = Temperature in Kelvin.
ENTROPY
T
q
S rev



15. SECOND LAW OF THERMODYNAMICS
The Second Law of Thermodynamics:
The Entropy of the universe does not
change for reversible processes and
increases for spontaneous processes.
Reversible (ideal) process:
Irreversible (real, spontaneous) process:
0
. 




 gs
surroundin
system
univ S
S
S
0
. 




 gs
surroundin
system
univ S
S
S

16. ―You can’t break even‖
SECOND LAW OF THERMODYNAMICS
Reversible (ideal) process:
Irreversible (real, spontaneous) process:
0
. 




 gs
surroundin
system
univ S
S
S
0
. 




 gs
surroundin
system
univ S
S
S

17. • The Entropy of the universe increases (real,
spontaneous processes).
• But, Entropy can decrease for individual systems.
SECOND LAW OF THERMODYNAMICS
Reversible (ideal) process:
Irreversible (real, spontaneous) process:
0
. 




 gs
surroundin
system
univ S
S
S
0
. 




 gs
surroundin
system
univ S
S
S

18. ENTROPY AT THE MOLECULAR SCALE
• Ludwig Boltzmann described the concept of
entropy at the molecular level.
• Temperature is a measure of the average
kinetic energy of the molecules in a sample.

19. The Austrian
Scientific Ludwig
Eduard Boltzmann
(1844 – 1906) has a
gravestone in Vienna
inscribed with his
famous relationship
between the Entropy
and the number of
available
Microstates:
S = k*lnW

20. Molecules exhibit several types of motion:
 Translational: Movement of the entire molecule
from one place to another.
 Vibrational: Periodic motion of atoms within a
molecule.
 Rotational: Rotation of the molecule on about an
axis or rotation about  bonds.
ENTROPY AT THE MOLECULAR SCALE

21. • Boltzmann envisioned the motions of a sample of
molecules at a particular instant in time.
 This would be akin to taking a snapshot of all the
molecules.
• He referred to this sampling as a MICROSTATE of the
thermodynamic system.
ENTROPY AT THE MOLECULAR SCALE

22. • Each thermodynamic state has a specific number
of microstates (W) associated with it.
• Entropy is: S = k*lnW
where k is the Boltzmann constant: 1.38*1023 J/K.
ENTROPY AT THE MOLECULAR SCALE

23. Implications:
• More particles:
 more states  more entropy
• Higher T:
 more energy states  more entropy
• Less structure (gas vs solid):
 more states  more entropy
ENTROPY AT THE MOLECULAR SCALE

24. The number of microstates and,
therefore, the entropy tends to
increase with increases in:
• Temperature.
• Volume (gases).
• The number of independently
moving molecules.
ENTROPY AT THE MOLECULAR SCALE

25. ENTROPY & PHYSICAL STATES
• Entropy increases
with the freedom
of motion of
molecules.
• Therefore,
S(g) > S(l) > S(s)

26. ENTROPY & SOLUTIONS
Usually, there is an overall increase in S.
(The exception is very highly charged ions that
make a lot of water molecules align around them.)
Dissolution of a solid:
Ions have more entropy
(more states). But,
some water molecules
have less entropy
(they are grouped
around ions).

27. SUMMARIZING ENTROPY CHANGES
In general, entropy
INCREASES when:
• Gases are formed
from liquids and
solids.
• Liquids or solutions
are formed from
solids.
• The number of gas
molecules
increases.
• The number of
moles increases.

28. 3RD LAW OF THERMODYNAMICS
The entropy of a pure crystalline
substance at absolute zero is 0.
0
1
ln
*
ln
* 

 k
W
k
S

29. 3RD LAW OF THERMODYNAMICS
The entropy of a pure crystalline
substance at absolute zero is 0.
0
1
ln
*
ln
* 

 k
W
k
S

30. STANDARD ENTROPIES
• These are molar
Entropy values of
substances in their
standard states.
• Standard Entropies
tend to increase with
increasing molar
mass.

31. Larger and more complex molecules
have greater Entropies!!!
STANDARD ENTROPIES

32. ENTROPY CHANGES
Entropy changes for a reaction can be
calculated the same way we used for H:
∆Srxn = ∆Sºproducts - ∆Sºreactants
• Standard-State Entropy (Sº) for each
component could found in Tables.
• Note: for pure elements:
0
0
0
0



H
S

33. Entropy Changes in Surroundings
• Heat that flows into or out of the system
also changes the entropy of the
surroundings.
• For an isothermal process:
• At constant pressure, qsys is simply H for
the system:
PRACTICAL USES:
SURROUNDINGS & SYSTEM
T
q
S
sys
surr 


T
H
T
q
S
sys
surr








34. LINKING S AND H: PHASE CHANGES
T
H
T
q
S
sys
surr







A phase change is isothermal (no change in T).
For water:
Hfusion = 6 kJ/mol
Hvap = 41 kJ/mol
If we do this reversibly:
Ssurr = – Ssys

35. Entropy Change in the Universe
• The universe is composed of the system
and the surroundings.
Therefore:
Suniverse = Ssystem + Ssurroundings
• For spontaneous processes:
Suniverse > 0
PRACTICAL USES:
SURROUNDINGS & SYSTEM

36. = – Gibbs Free Energy
PRACTICAL USES:
SURROUNDINGS & SYSTEM





 system
system
universe H
S
T
S
T
Starting from the Entropy Change in the Universe:
And considering that:
We get the following expression:
Multiplying by T we get:
gs
surroundin
system
universe S
S
S 




T
H
Ssurr





)
( T
H
system
universe
system
S
S








37. Make this equation nicer:
PRACTICAL USES:
SURROUNDINGS & SYSTEM
= – Gibbs Free Energy





 system
system
universe H
S
T
S
T
system
system
universe S
T
H
S
T 




 
system
system S
T
H
G 



 

38. T∆Suniverse is defined as the Gibbs Free
Energy (G).
For spontaneous processes: Suniverse > 0
And therefore: G < 0
G is easier to determine than Suniverse.
So: Use G to decide if a process is
spontaneous.
PRACTICAL USES: SURROUNDINGS
& SYSTEM: GIBBS FREE ENERGY

39. The American Scientist Josiah Willard Gibbs (1839 – 1903)
made important contributions to thermodynamics. He was
the first person to be awarded a PhD. in Sciences from an
American University (Yale 1863).
∆G = ∆H - T ∆S

40. GIBBS FREE ENERGY
1.If G is negative,
the forward reaction
is spontaneous.
2.If G is 0, the
system is at
equilibrium.
3.If G is positive, the
reaction is
spontaneous in the
reverse direction.

41. STANDARD FREE ENERGY CHANGES
• Standard Free Energies of
Formation, Gfº are analogous to
Standard Enthalpies of Formation
(Hfº):
∆Gfº = ∆Gºproducts – ∆Gºreactants
• G can be looked up in tables, or
calculated from S° and H°

42. FREE ENERGY CHANGES
Very key equation:
This equation shows how Gº
changes with temperature.
Note: We will assume that Sº & Hº
are independent of T.
system
system S
T
H
G 





 

43. FREE ENERGY AND TEMPERATURE
• There are two parts to the Free
Energy equation:
 H — the Enthalpy term; and
 TS — the Entropy term.
• The temperature dependence of
Free Energy comes from the
Entropy term.

44. FREE ENERGY AND TEMPERATURE
By knowing the sign (+ or —) of S and
H, we can get the sign of G and
determine if a reaction is spontaneous.

45. FREE ENERGY AND EQUILIBRIUM
Remember from above:
If ∆G is 0, the system is at equilibrium.
So ∆G must be related to the
equilibrium constant (Keq-Chapter 15).
The Standard Free Energy (∆Gº) is
directly linked to Keq by:
∆Gº = — RT lnKeq or ∆Gº = — RT lnK
Note: for pure elements:
0
0
0
0
0
0





G
H
S

46. SUMMARIZING FREE ENERGY
1.The Free Energy (∆G) is negative for all
spontaneous processes.
2.The Free Energy (∆G = 0) for any system at
equilibrium.
3.The Free Energy (∆G) is positive for non
spontaneous processes.

48. • When a system in a given initial state goes
through a number of different changes in
state and finally returns to its initial values,
the system has undergone a cycle.
• Therefore, at the conclusion of a cycle, all
the properties have the same value they had
at the beginning.
• E.g. steam that circulates through a closes
cooling room undergoes a cycle.
CYCLICAL PROCESS

49. The term PHASE CHANGE indicates that a
substance has changed among the three classical
phases of matter: solid, liquid, gas and plasma:
• Solid to liquid – Melting;
• Liquid to solid – Freezing;
• Liquid to gas – Boiling;
• Gas to liquid – Condensation;
• Solid to gas – Sublimation;
• Gas to solid – Deposition.
PHASE PROCESSES

50. STATE CHANGES

52. • A Thermodynamic State is a set of values of
properties of a thermodynamic system that
must be specified to reproduce the system.
• The individual parameters are known as state
variables, state parameters or thermodynamic
variables.
• Once a sufficient set of thermodynamic
variables have been specified, values of all
other properties of the system are uniquely
determined. The number of values required to
specify the state depends on the system, and is
not always known.
STATE CHANGES

53. • An isothermal process occurs at a constant
temperature.
• An example would be to have a system
immersed in a large constant temperature
bath. Any work energy performed by the
system will be lost to the bath, but its
temperature will remain constant. In other
words, the system is thermally connected,
by a thermally conductive boundary to a
constant temperature reservoir.
ISOTHERMAL PROCESS

54. • An isochoric (or iso-volumetric) process is one in
which the volume is held constant, meaning that the
work done by the system will be zero.
• It follows that, for the simple system of two
dimensions, any heat energy transferred to the
system externally will be absorbed as internal
energy.
• An example would be to place a closed tin can
containing only air into a fire. To a first
approximation, the can will not expand, and the only
change will be that the gas gains internal energy, as
evidenced by its increase in temperature and
pressure. We may say that the system is dynamically
insulated, by a rigid boundary, from the
environment.
ISOCHORIC PROCESS

55. • An isobaric process is a thermodynamic process
in which the pressure remains constant.
• This is usually obtained by allowing the volume
to expand or contract in such a way to neutralize
any pressure changes that would be caused by
heat transfer.
• In an isobaric process, there are typically
internal energy changes, work is done by the
system, and heat is transferred, so none of the
quantities in the First Law of Thermodynamics
readily reduce to zero.
ISOBARIC PROCESS

56. SUMMARIZING
a. An isobaric process is one in which the
pressure remains constant.
b. An isochoric process is one in which the
volume remains constant.
c. An Isothermal process is which that happens
at a constant temperature.

57. CONCLUSIONS (1)
1. The Second Law of Thermodynamics states
that in any spontaneous process the Entropy
of the universe increases.
2. The Third Law of Thermodynamics states
that the Entropy of a pure crystalline solid at
absolute zero (0 K) is zero.
3. Entropy is an indicative of the randomness of
a system. Entropy is a state function like
Internal Energy and Enthalpy.
4. The Entropy of any system tends to increase
with increases in Temperature, Volume and
the number of moving molecules.

58. CONCLUSIONS (2)
4.The Gibbs Free Energy is a potential that
measures the maximum or reversible work that
may be performed by a thermodynamic system
at a constant temperature and pressure
(isothermal and isobaric). As such, a reduction
in Free Energy is a necessary condition for the
spontaneity of processes at constant pressure
and temperature.
5.The Gibbs Free Energy of the system is a state
function because it is defined in terms of
thermodynamic properties that are state
functions (Entropy and Enthalpy).