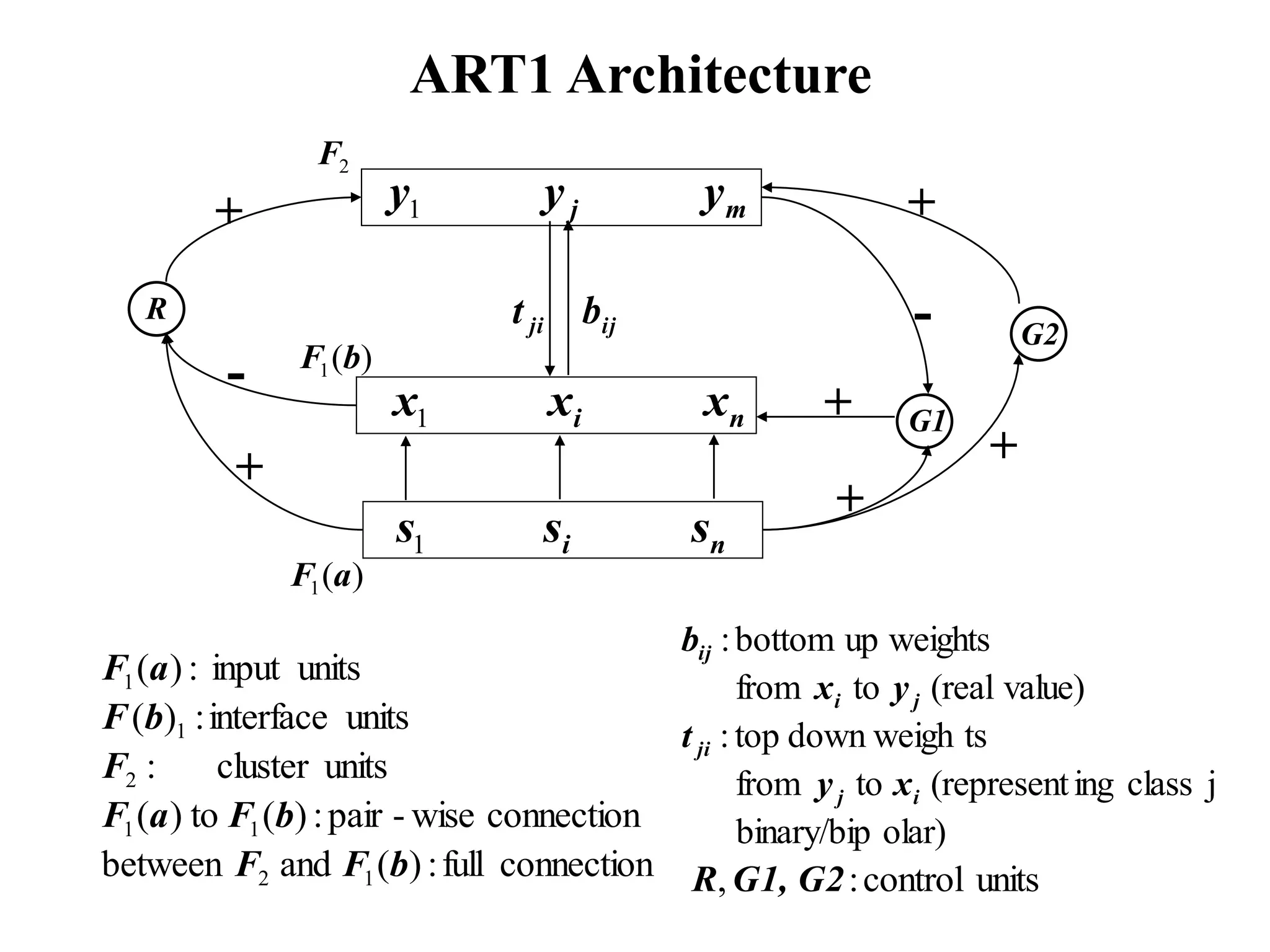
This document summarizes Adaptive Resonance Theory (ART), which was developed to allow neural networks to incrementally learn new patterns without forgetting old ones. ART1 is designed for binary patterns and ART2 for continuous patterns. The key ideas are to find the most similar existing cluster for a new input, and if it is not sufficiently similar, create a new cluster. The architecture uses input, cluster, and interface units connected by adaptive weights to classify inputs through resonance or create new clusters when needed.

1. Chapter 5. Adaptive Resonance Theory (ART)
• ART1: for binary patterns; ART2: for continuous patterns
• Motivations: Previous methods have the following problem:
1. Training is non-incremental:
– with a fixed set of samples,
– adding new samples often requires re-train the network with
the enlarged training set until a new stable state is reached.
2. Number of class nodes is pre-determined and fixed.
– Under- and over- classification may result from training
– No way to add a new class node (unless these is a free
class node happens to be close to the new input).
– Any new input x has to be classified into one of an existing
classes (causing one to win), no matter how far away x is
from the winner. no control of the degree of similarity.

2. • Ideas of ART model:
– suppose the input samples have been appropriately classified
into k clusters (say by competitive learning).
– each weight vector is a representative (average) of all
samples in that cluster.
– when a new input vector x arrives
1.Find the winner j among all k cluster nodes
2.Compare with x
if they are sufficiently similar (x resonates with class j),
then update based on
else, find/create a free class node and make x as its
first member.
j
W
j
W
j
W j
W
x 


3. • To achieve these, we need:
– a mechanism for testing and determining similarity.
– a control for finding/creating new class nodes.
– need to have all operations implemented by units of
local computation.

4. ART1 Architecture
n
i s
s
s1
m
j y
y
y1
ij
b
ji
t
R
G2
)
(
1 a
F
2
F
connection
full
:
)
(
and
between
connection
wise
-
pair
:
)
(
to
)
(
units
cluster
:
units
interface
:
)
(
units
input
:
)
(
1
2
1
1
2
1
1
b
F
F
b
F
a
F
F
b
F
a
F
olar)
binary/bip
j
class
ing
(represent
to
from
ts
down weigh
top
:
value)
(real
to
from
weights
up
bottom
:
i
j
ji
j
i
ij
x
y
t
y
x
b
units
control
:
,G1, G2
R
+
+
+
+
+
-
-
+ G1
)
(
1 b
F
n
i x
x
x1

5. • cluster units: competitive, receive input vector x
through weights b: to determine winner j.
• input units: placeholder or external inputs
• interface units:
– pass s to x as input vector for classification by
– compare x and
– controlled by gain control unit G1
•
• Needs to sequence the three phases (by control units G1,
G2, and R)
2
F
)
winner
from
n
(projectio j
j y
t 
1
G
)
(
1 a
F
)
(
1 b
F
2
F
1)
are
inputs
three
the
of
two
if
1
(output
rule
2/3
obey
and
)
(
both
in
Nodes 2
1 F
b
F
R
G
t
F
t
G
s
b
F ji
ji
i ,
2
,
:
Input to
,
1
,
:
)
(
Input to 2
1

6. 





 


J
t
b
F
G
s
b
F
G
y
s
G
for
open
)
(
:
0
0
receive
open to
)
(
:
1
otherwise
0
0
and
0
if
1
1
1
1
1
1
parameter
vigilance
1
otherwise
1
if
0











o
s
x
R
input
new
a
for
tion
classifica
new
a
of
start
the
signals
1
otherwise
0
0
if
1
2
2



 

G
s
G
R = 0: resonance occurs, update and
R = 1: fails similarity test, inhibits J from further computation

J
t
J
b

7. Working of ART1
• Initial state:nodes on set to zeros
• Recognition phase: determine the winner cluster for input s
2
1 and
)
( F
b
F
J
b
x
F
s
x
R
s
b
F
s
G
s
y
G
a
F
s
j
winner
determine
receive
to
open
is
)
1
/
(
0
receive
to
open
is
)
(
)
0
(
1
)
0
,
0
(
1
(clamped)
there
stay
and
)
(
to
applied
is
0
2
1
2
1
1














0
1
cluster
to
classified
ly
tentative
is

 J
k
J Y
Y
J
x

8. • Comparison phase:
match
possible
other
for
search
phase
n
recognitio
back to
goes
zero
set to
is
other
all
disabled
y
permanentl
is
)
to
(from
sent
is
signal
reset
rejected
is
tion
classifica
1
/
if
accepted
is
tion
classifica
the
occurs,
resonance
a
0
/
if
)
rule
2/3
(
:
)
(
on
appears
new
)
0
(
0
from
down
sent
is
2
1
1
2
k
J
Ji
i
i
J
y
y
F
R
R
s
x
R
s
x
t
s
x
b
F
x
y
G
F
t












9. • Weight update/adaptive phase
– Initial weight: (no bias)
bottom up:
top down:
– When a resonance occurs with
– If k sample patterns are clustered to node then
= pattern whose 1’s are common to all these k samples
2)
usually
(
)
1
/(
)
0
(
0 L
n
L
L
bij 



1
)
0
( 
ji
t

 J
J
J t
b
y and
update
,
Ji
i
i
J
t
s
x
b
F
t
s
x
a
F
s


 )
)
(
(on
and
between
result
comparison
:
)
)
(
(on
input
current
:
1
1
x
L
Lx
b
x
t i
ij
i
Ji




1
new
new
.
J
y
J
t
J
J
J
i
i
J
J
t
b
x
t
s
x
b
k
s
s
s
t











normalized
a
is
,
0
if
only
0
iff
0
)
new
(
)
(
).....
2
(
)
1
(

10. – Winner may shift:















3
1
)
0
1
1
1
(
)
1
(
)
0
0
0
1
(
)
0
0
0
1
(
)
3
(
)
0
0
1
1
(
)
0
0
1
1
(
)
2
(
)
0
1
1
1
(
)
0
1
1
1
(
)
1
(
2
.
0
)
0
(
,
2
1
1
1
s
x
s
t
s
t
s
t
s
b
L ij
– What to do when failed to classify into any existing
cluster?
– report failure/treat as outlier
– add a new cluster node
1
,
1
,
1
1
, 


 
 i
m
m
i t
n
L
L
b
with
1

m
y

11. Notes
1. Classification as a search process
2. No two classes have the same b and t
3. Different ordering of sample input presentations may result
in different classification.
4. Increase of  increases # of classes learned, and decreases
the average class size.
5. Classification may shift during search, will reach stability
eventually.
6. ART2 is the same in spirit but different in details.