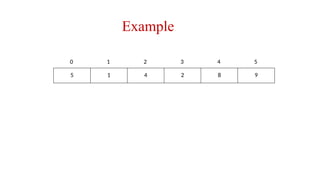
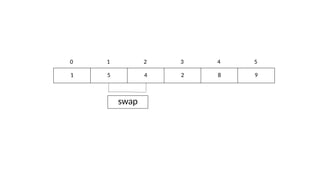
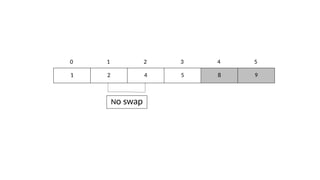
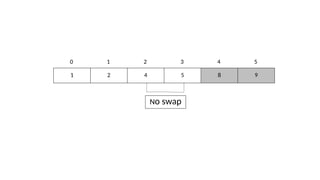
The document explains sorting and bubble sort, a simple comparison-based algorithm that arranges data in ascending or descending order by repeatedly comparing and swapping adjacent elements. It provides a detailed implementation process along with a code snippet in C++. Additionally, the document discusses the time complexity of bubble sort, which is O(n^2).

1. Analysis OF Algorithm

2. Bubble Sort

3. Learning outcomes
• What is sorting?
• What is bubble sort?

4. What is Sorting?
• Sorting is a process of arranging the values of array in a
particular order.
• A process that organizes a collection of data into either
ascending or descending order
• An array can be sorted in two orders:
 Ascending Order
 Descending Order
Data Structure

5. • Ascending Order
• In ascending order, the smallest value is stored in the first element
of array, second smallest value is stored in the second element and
so on. The largest value is stored in the last element.
• Descending Order
• In descending order, the largest value is stored in the first element
of arrays, second largest value is stored in the second element and
so on. The smallest value is stored in the last element.
Data Structure
Arrangement of Element Can Be

6. Bubble Sort Algorithm
• Bubble Sort is a simple algorithm which is used to sort a
given set of (N) elements.
• Bubble sort is also known as exchange sort.
• This sorting algorithm is comparison based algorithm in
which each pair of adjacent elements is compared and
elements are swapped if they are not in order.
• If we have total (N) elements, then we need to repeat this
process for (N-1) times.
Data Structure

7. Implementing Bubble Sort Algorithm
1. Starting with the first element(index = 0), compare the
current element with the next element of the array.
2. If the current element is greater than the next element of
the array, swap them.
3. If the current element is less than the next element, move
to the next element.
Data Structure

8. 5 1 4 2 8 9
0 1 2 3 4 5
Data Structure
Example

9. swap
5 1 4 2 8 9
0 1 2 3 4 5
Data Structure

10. swap
1 5 4 2 8 9
0 1 2 3 4 5
Data Structure

11. swap
1 5 4 2 8 9
0 1 2 3 4 5
Data Structure

12. 1 4 5 2 8 9
0 1 2 3 4 5
Data Structure

13. swap
1 4 5 2 8 9
0 1 2 3 4 5
Data Structure

14. No swap
1 4 2 5 8 9
0 1 2 3 4 5
Data Structure

15. No swap
1 4 2 5 8 9
0 1 2 3 4 5
Data Structure

16. 1 4 2 5 8 9
0 1 2 3 4 5
No swap
Data Structure

17. 1 4 2 5 8 9
0 1 2 3 4 5
swap
Data Structure

18. 1 2 4 5 8 9
0 1 2 3 4 5
No swap
Data Structure

19. 1 2 4 5 8 9
0 1 2 3 4 5
No swap
Data Structure

20. 1 2 4 5 8 9
0 1 2 3 4 5
Data Structure

21. 1 2 4 5 8 9
0 1 2 3 4 5
No swap
Data Structure

22. 1 2 4 5 8 9
0 1 2 3 4 5
No swap
Data Structure

23. 1 2 4 5 8 9
0 1 2 3 4 5
No swap
Data Structure

24. 1 2 4 5 8 9
0 1 2 3 4 5
No swap
Data Structure

25. 1 2 4 5 8 9
0 1 2 3 4 5
No swap
Data Structure

26. 1 2 4 5 8 9
0 1 2 3 4 5
No swap
Data Structure

27. • The Sorted List:
1 2 4 5 8 9
0 1 2 3 4 5
1 2 4 5 8 9
0 1 2 3 4 5
Data Structure

28. Visual Representation

29. Time Complexity
Number OF Swapping
(N-1)
(N-2)
.
.
.
3
2
1
Time Complexity: (N-1) + (N-2) + … +3+2+1
= N(N-1)/2
= O(N2
)
6 5 4 3 2 1
6 5 4 3 2 1
5 4 3 2 1 6
4 3 2 1 5 6
3 2 1 4 5 6
2 1 3 4 5 6
0 1 2 3 4 5
S S S S S 5
4
3
2
1
S S
S S
S S S
S S
S

30. Code snippet
#include<iostream>
using namespace std;
int main() {
int size,i,j,temp;
cout<<"Enter The size of array:n"; cin>>size;
int arr[size]; cout<<"Enter The Elements:n";
for(i=0;i<size;i++){ cin>>arr[i]; }
cout<<"Before Sorting:"<<endl;
for(i=0;i<size;i++){ cout<<arr[i]<<"t"; }
Data Structure

31. Code snippet
for(i=0;i<size;i++){
for(j=0;j<size-1;j++){
if(arr[j]>arr[j+1]){
temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp; }
cout<<"n After Sorting:"<<endl;
for(i=0;i<size;i++)
cout<<arr[i]<<"t";
}
Data Structure

32. Thank You!!!