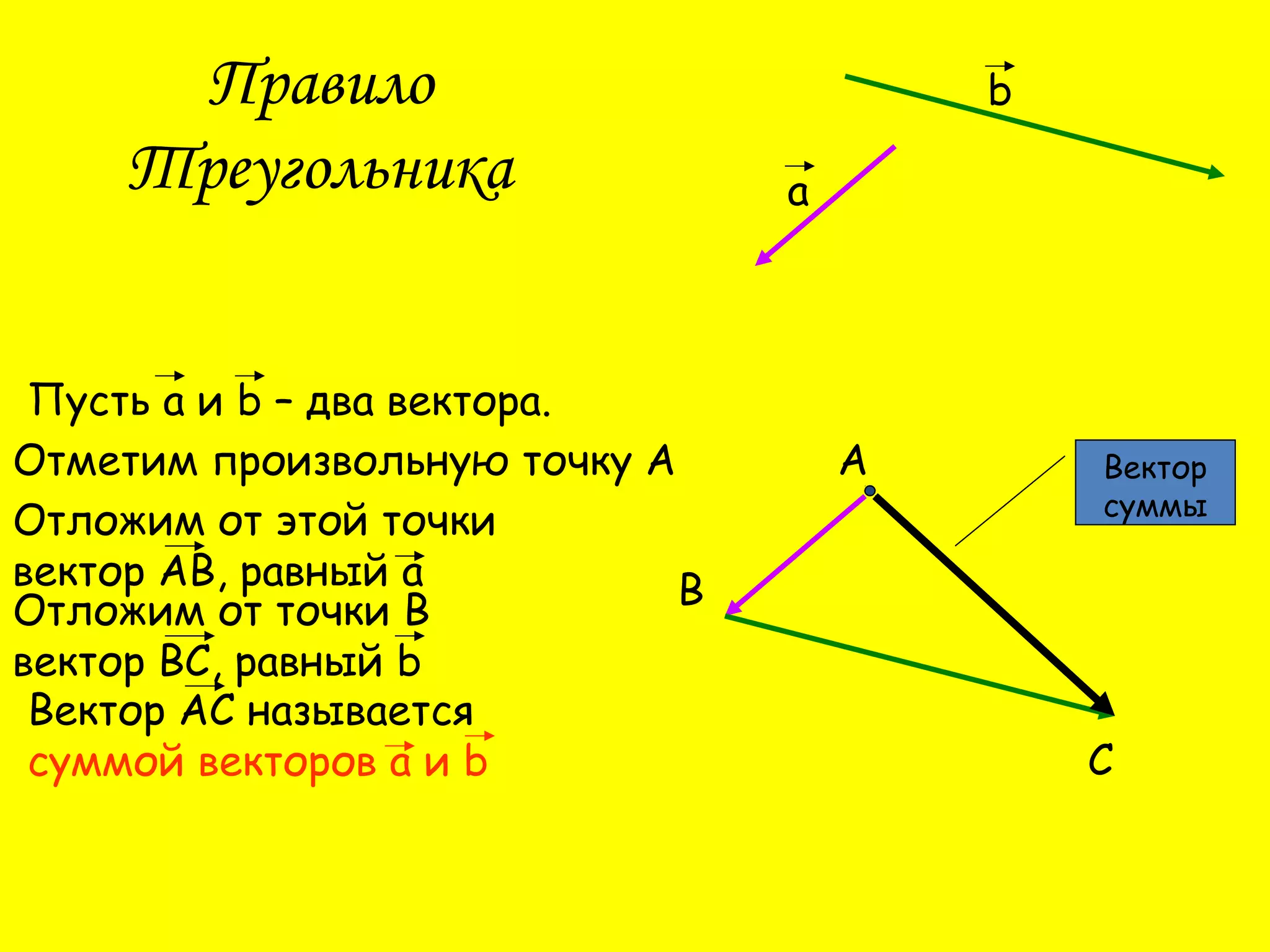
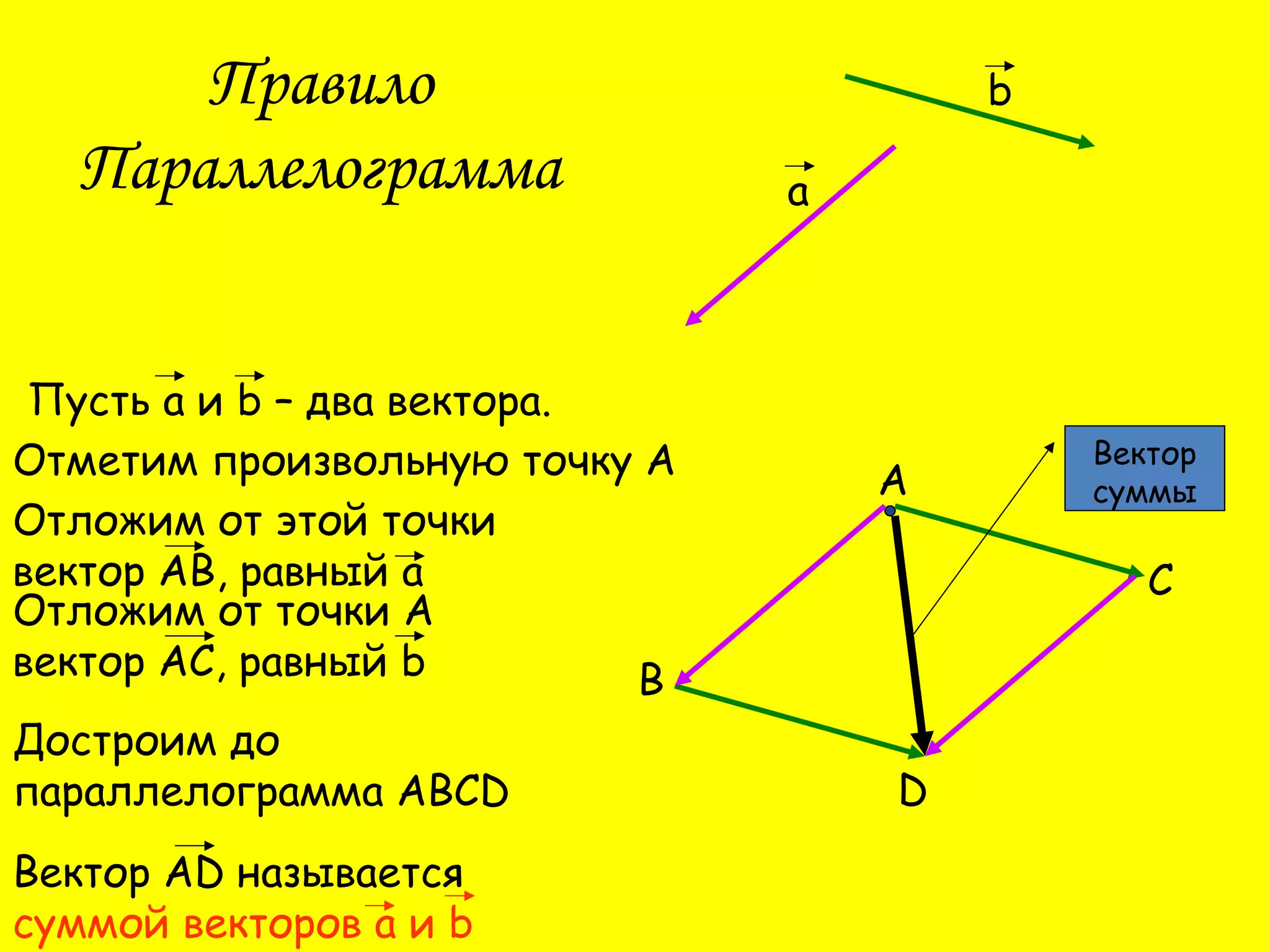
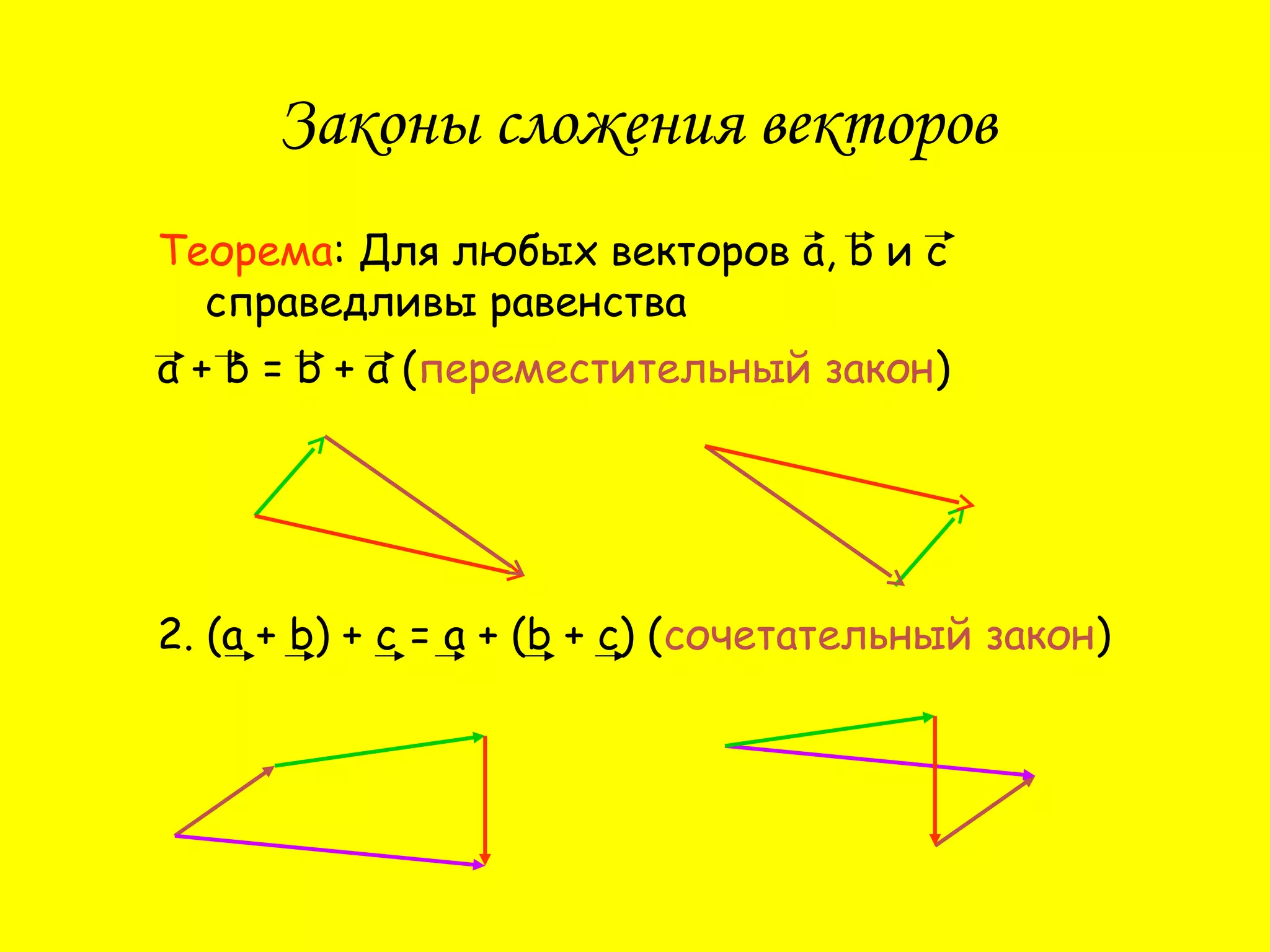
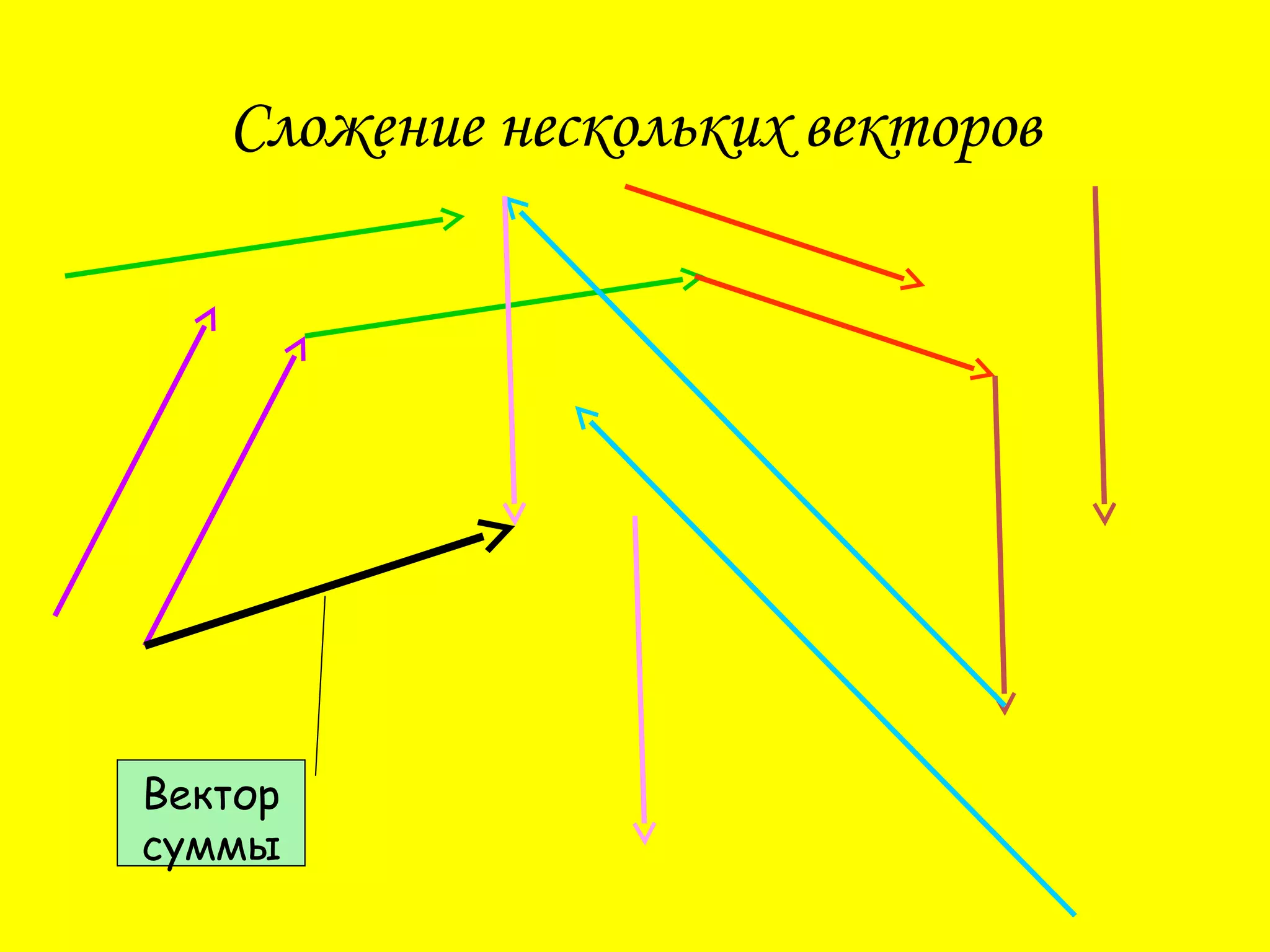
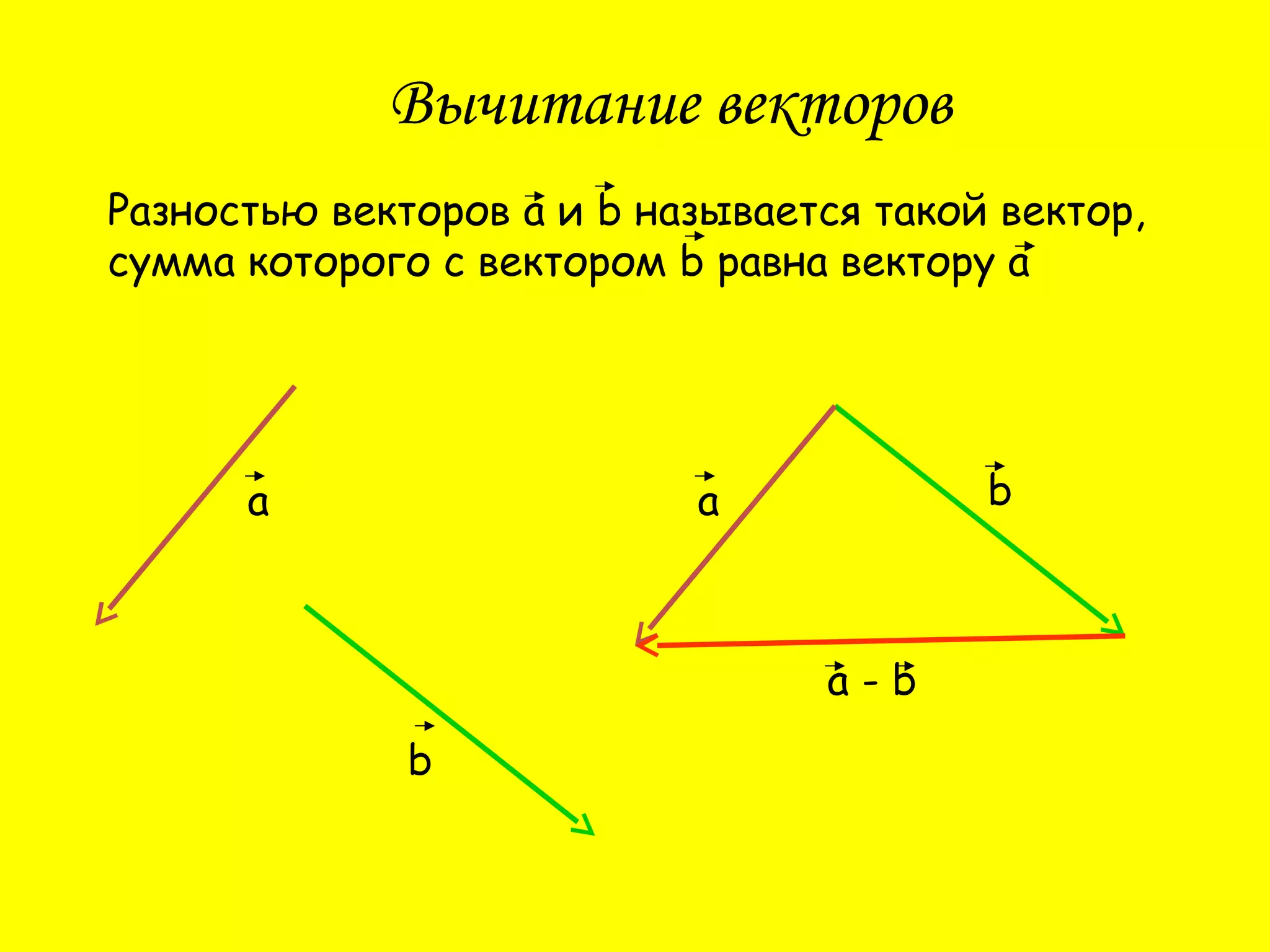
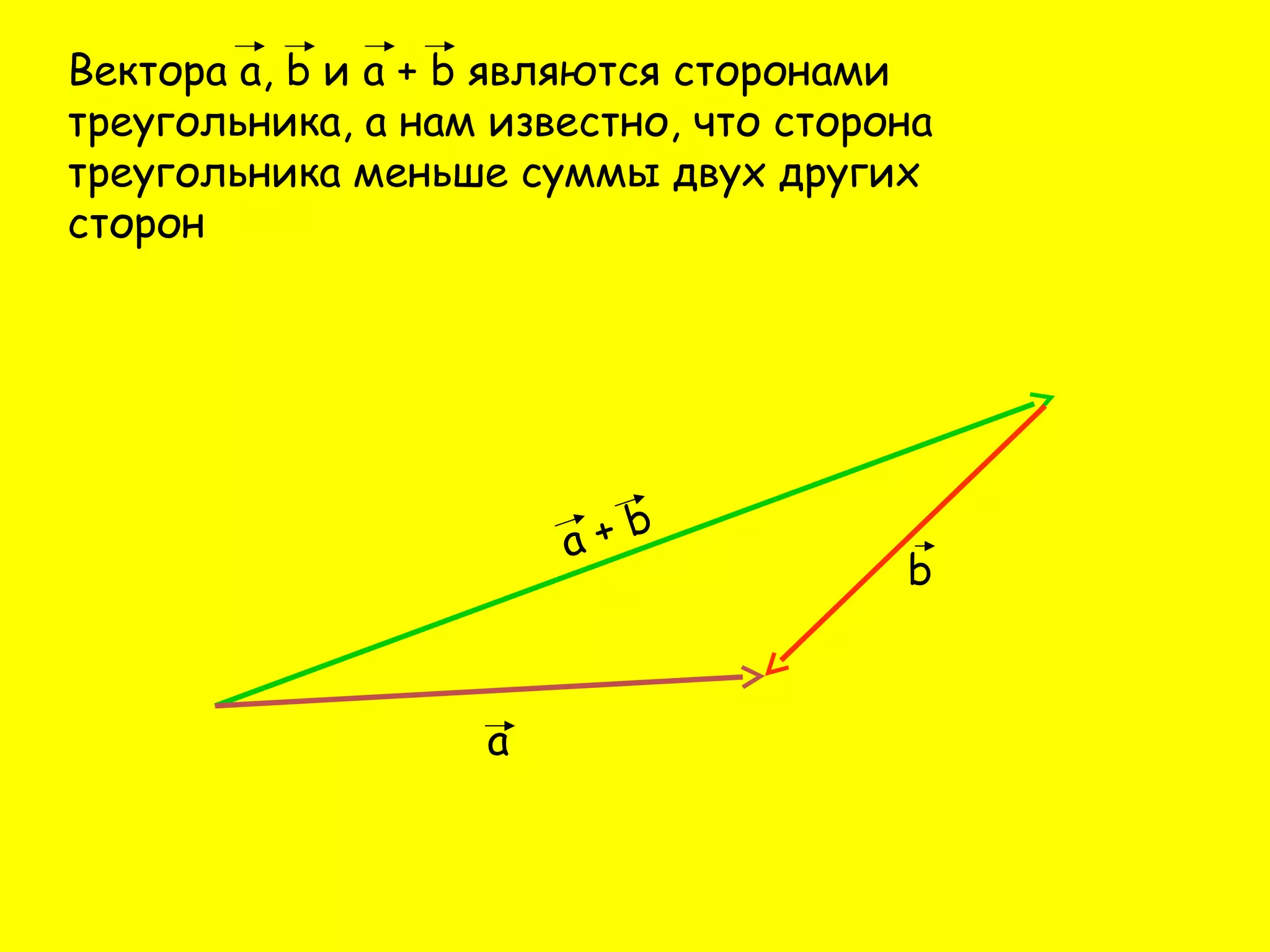
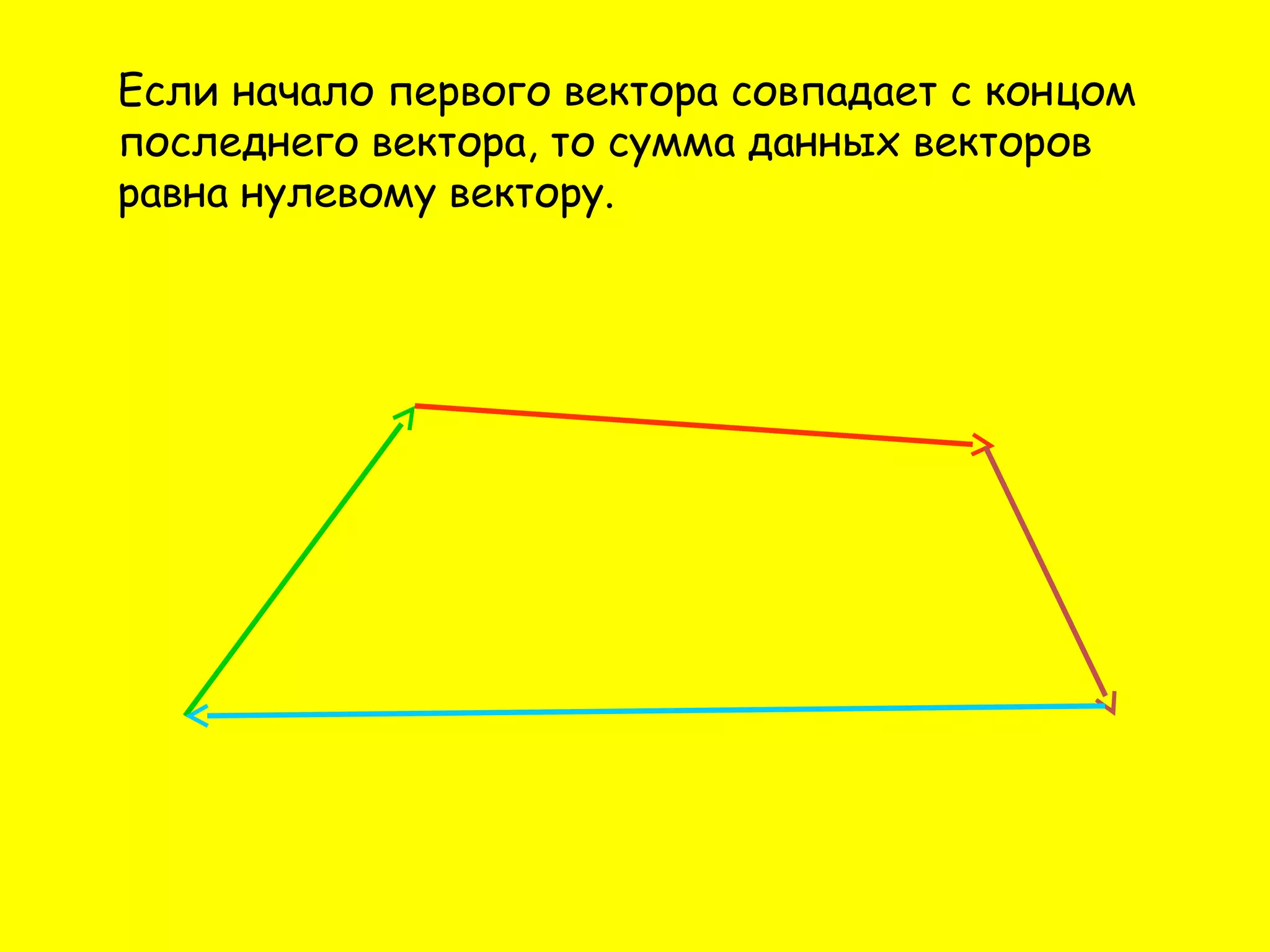
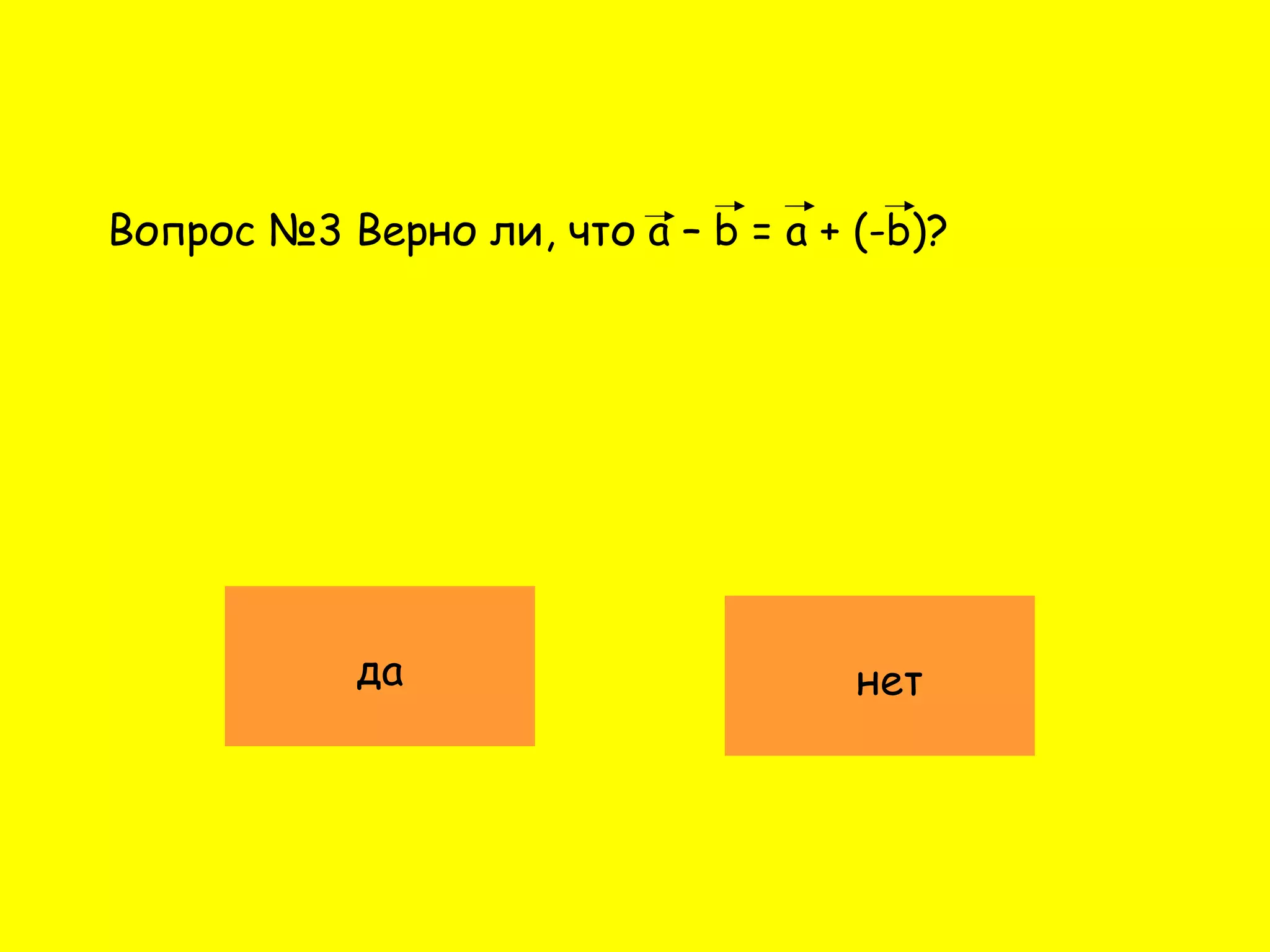
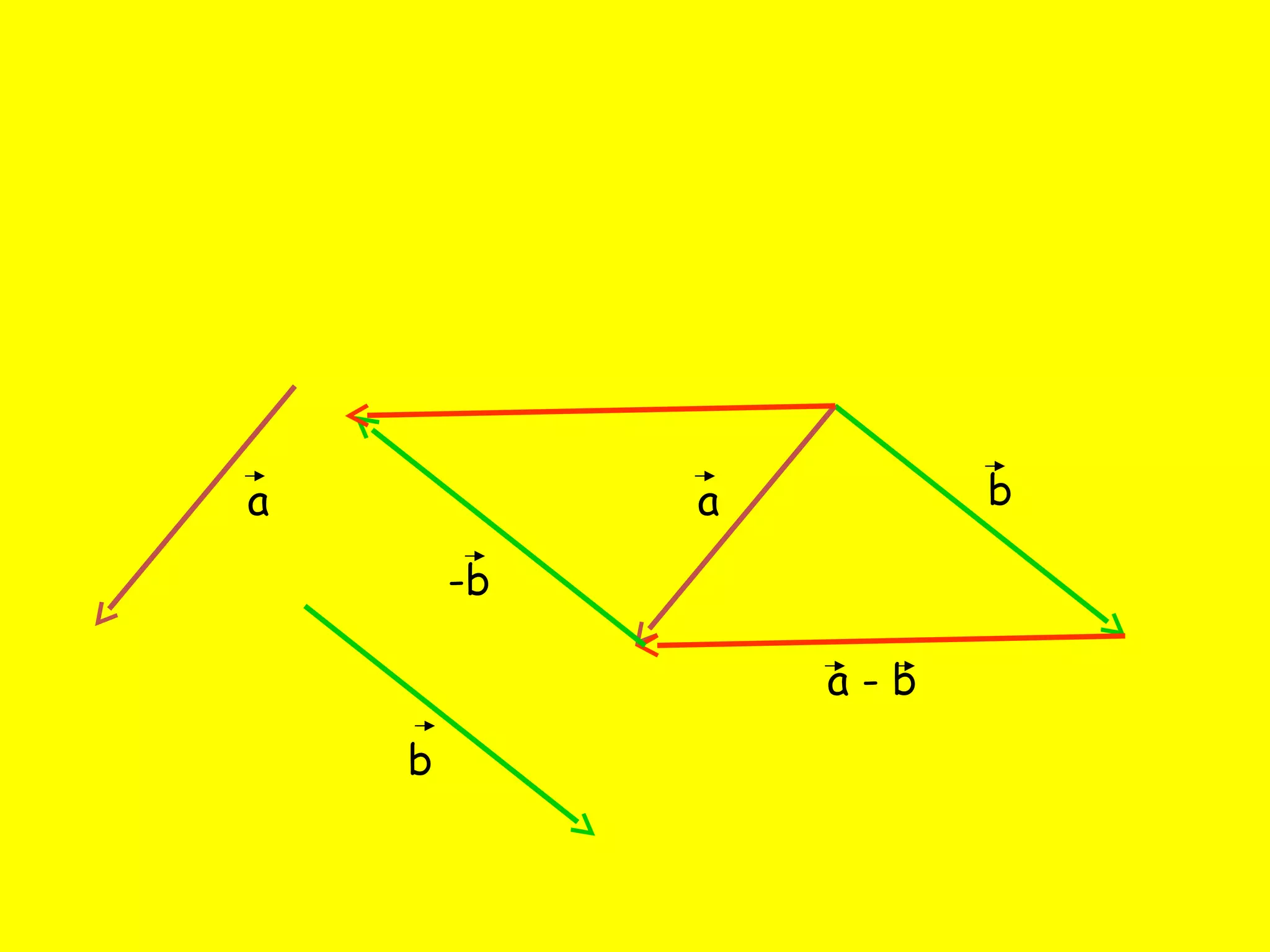
Документ описывает операции сложения и вычитания векторов, а также правила их выполнения, такие как правило треугольника и правило параллелограмма. Приводятся законы сложения векторов, включая переместительный и сочетательный закон. Также содержатся тестовые вопросы для проверке понимания темы.