Statistics formula
•Download as PPTX, PDF•
3 likes•404 views
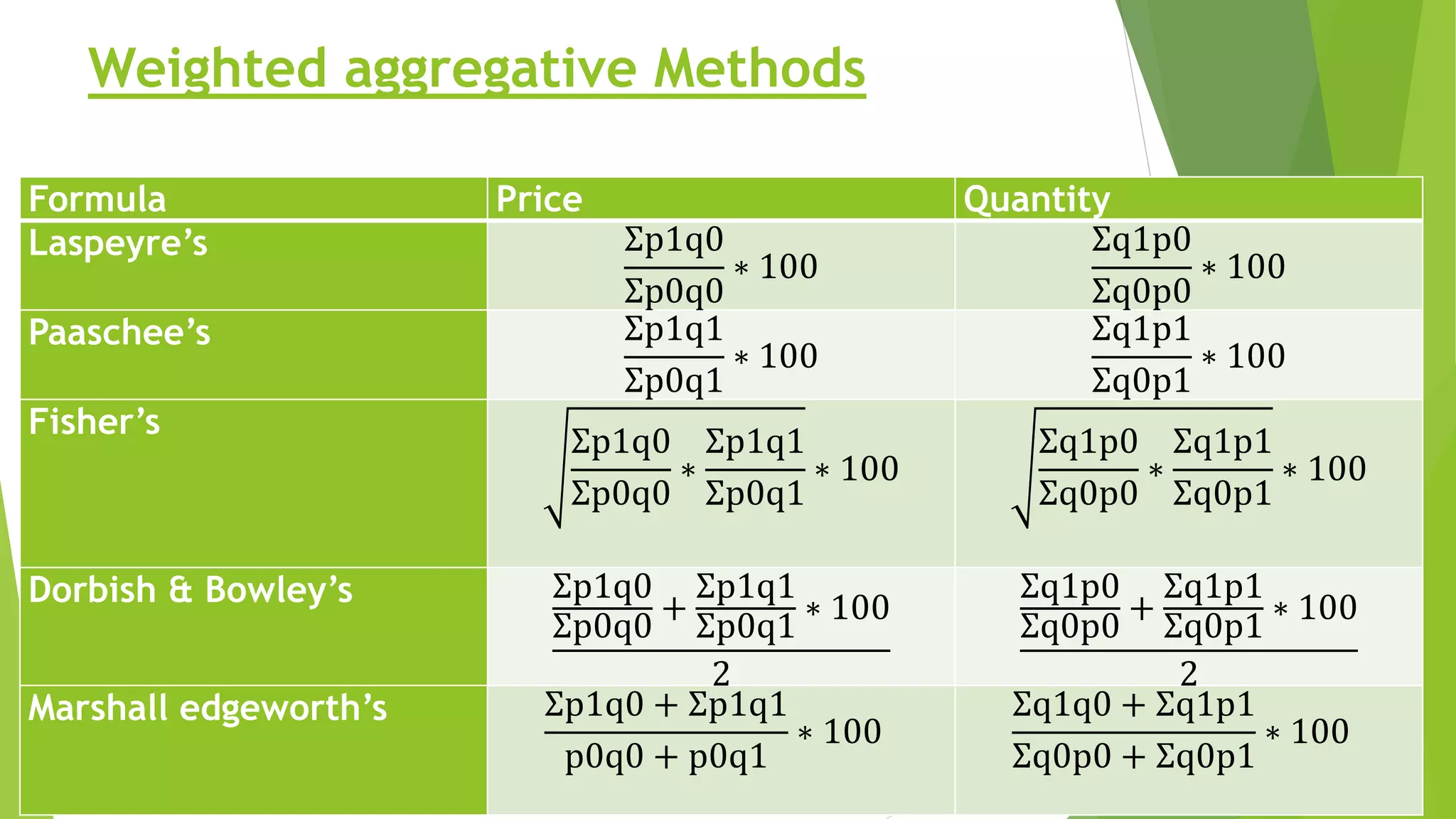
The document contains formulas and explanations for various statistical concepts including: 1) Mean, median, mode, and weighted mean formulas for individual discrete, continuous, and combined data. 2) Standard deviation formulas including direct, short cut, and step deviation methods for individual and combined discrete and continuous data. 3) Formulas for other concepts like correlation, regression, time series analysis, index numbers, and skewness. 4) Explanations of techniques like least squares method, time reversal test, and factor reversal test as they apply to various statistical analyses.
More Related Content
What's hot
What's hot (20)
Similar to Statistics formula
Recently uploaded
Recently uploaded (20)
Statistics formula
- 1. STATISTICS FORMULA Harimohan 17PBA019 Baddi University of emerging sciences and technology
- 2. Mean Formula Individual Discrete Continuous DIRECT 𝛴𝑋 𝑁 𝛴𝑓𝑋 𝑁 𝛴𝑓𝑚 𝑁 SHORT CUT A+ 𝛴𝑑 𝑁 A+ 𝛴𝑓𝑑 𝑁 A+ 𝛴𝑓𝑑 𝑁 STEP DEVIATION A+ 𝛴𝑓𝑑′ 𝑁 ∗ 𝑖 A+ 𝛴𝑓𝑑 𝑁 ∗ i (d=X-X͞ )
- 3. Mean COMBINED MEAN 𝑵 𝟏X͞ 𝟏+𝑵 𝟐X͞ 𝟐 𝑵𝟏+𝑵𝟐 , WEIGHTED MEAN ∑𝑾𝑿 ∑𝑾
- 4. Median Individual N+1/2 (when in points add L+U/2) Continuous M= L+ 𝑁 2 −𝑐𝑓 𝑓 ∗ 𝑖
- 6. QUARTILE DEVIATION Individual Continuous Q1= 𝑁+1 4 Q3= 3 𝑁+1 4 QD= 𝑄3−𝑄1 2 , QD=𝐿 + 𝑁 4 −𝑐𝑓 𝑓 ∗ 𝑖 Coeff. = 𝑄3−𝑄1 𝑄3+𝑄1
- 7. MEAN DEVIATION Individual Discrete & CONTINOUS COFFICENT MD= 𝛴│𝑑 𝑁 MD= 𝛴𝑓│𝑑│ 𝑁 𝑀𝐷 𝑀𝐸𝐷𝐼𝐴N 𝑂𝑅 𝑀𝐸𝐴𝑁
- 8. STANDARD DEVIATION DIRECT SHORT CUT STEP DEVIATION Individual =SD= 𝚺𝐗 𝟐 𝐍 OR 𝚺(𝐗−𝐗͞ 𝐍 𝚺𝐝𝐱 𝟐 𝐍 − ( 𝚺𝐝𝐱 𝐍 )² = 𝚺𝐝𝐱 𝟐 𝐍 − ( 𝚺𝐝𝐱 𝐍 )² ∗ 𝐂 Discrete & continuous 𝚺𝐟𝐝𝐱² 𝐍 − ( 𝚺𝐟𝐝𝐱 𝐍 )² 𝚺𝐝𝐱′ 𝟐 𝐍 − ( 𝚺𝐝𝐱′ 𝐍 )² ∗ 𝐂 dx’= 𝐝𝐱 𝐂
- 9. STANDARD DEVIATION Coefficient of SD= ϭ 𝑋 AND Coefficient of variation or C.V = ϭ 𝑋 ∗ 100 Combined SD= 𝑵 𝟏ϭ 𝟏+𝑵 𝟐ϭ 𝟐+𝑵 𝟏 𝒅 𝟏+𝑵₂𝒅₂ 𝑵 𝟏+𝑵₂
- 10. SKEWNESS Karl pearson Bowleey Kelly 𝐦𝐞𝐚𝐧 − 𝐦𝐨𝐝𝐞 𝑺𝑫 𝑸𝟑 + 𝑸𝟏 − 𝟐 𝑴𝑬𝑫𝑰𝑨𝑵 𝑸𝟑 − 𝑸𝟏 𝒅𝟗 + 𝒅𝟏 − 𝟐𝒎𝒆𝒅 𝒅𝟗 − 𝒅𝟏
- 11. INDEX NUMBER Simple Methods Formula Price Quantity Simple aggregative Σp1 Σp0 ∗ 100 Σq1 Σq0 ∗ 100 Price Relative Σ p1 p0 ∗ 100 N Σ q1 q0 ∗ 100 N
- 12. Weighted aggregative Methods Formula Price Quantity Laspeyre’s Σp1q0 Σp0q0 ∗ 100 Σq1p0 Σq0p0 ∗ 100 Paaschee’s Σp1q1 Σp0q1 ∗ 100 Σq1p1 Σq0p1 ∗ 100 Fisher’s Σp1q0 Σp0q0 ∗ Σp1q1 Σp0q1 ∗ 100 Σq1p0 Σq0p0 ∗ Σq1p1 Σq0p1 ∗ 100 Dorbish & Bowley’s Σp1q0 Σp0q0 + Σp1q1 Σp0q1 ∗ 100 2 Σq1p0 Σq0p0 + Σq1p1 Σq0p1 ∗ 100 2 Marshall edgeworth’s Σp1q0 + Σp1q1 p0q0 + p0q1 ∗ 100 Σq1q0 + Σq1p1 Σq0p0 + Σq0p1 ∗ 100
- 13. INDEX NUMBERS Time Reversal Test : P01 X P10 = 1 Factor Reversal Test P01 XQ01 = ΣP1q1/ΣP0q0
- 14. CORELATION (Actual mean) Assumed mean) Actual data r= 𝛴𝑥𝑦 𝛴𝑥2.𝛴𝑦2 r= 𝑁.𝛴𝑑𝑥𝑑𝑦−𝛴𝑑𝑥.𝛴𝑑𝑦 𝑁𝛴𝑑𝑥²− 𝛴𝑑𝑥 2. 𝑁.𝛴𝑑𝑦²−(𝛴𝑑𝑦)² r= 𝑁.𝛴𝑋𝑌−𝛴𝑋.𝛴𝑌 𝑁.𝛴𝑋²− 𝛴𝑋 2. 𝛴𝑌²−(𝛴𝑌)²
- 15. When ranks are not given
- 17. REGRESSION 1.Y on X Y=a+ bX ΣY=Na+bΣx ΣXY=aΣX+bΣX² 2.X on Y X=a+ bY ΣX=Na+bΣY ΣXY=aΣY+bΣY²
- 18. Equation using coefficient (Using Mean) 1.Y on X Y-Y̅=byx(X- X̅) byx= 𝑁.𝛴𝑥𝑦−𝛴𝑥.𝛴𝑦 𝑁.𝛴𝑥²−(𝛴𝑥)² 2.X on Y X-X̅=bxy(Y- Y̅) bxy= 𝑁.𝛴𝑥𝑦−𝛴𝑦.𝛴𝑥 𝑁.𝛴𝑦²−(𝛴𝑦)²
- 19. Assumed mean 1.Y on X Y-Y̅=byx(X-X̅) byx= 𝑁.𝛴𝑑𝑥𝑑𝑦−𝛴𝑑𝑥.𝛴𝑑𝑦 𝑁.𝛴𝑑𝑥²−(𝛴𝑑𝑥)² 2. X on Y X-X̅=bxy(Y-Y̅) bxy= 𝑁.𝛴𝑑𝑥𝑑𝑦−𝛴𝑑𝑦.𝛴𝑑𝑥 𝑁.𝛴𝑑𝑦²−(𝛴𝑑𝑦)²
- 20. Time series Least square method yс = a +bx if x =0 then a = ∑y 𝑁 b = ∑xy ∑x²