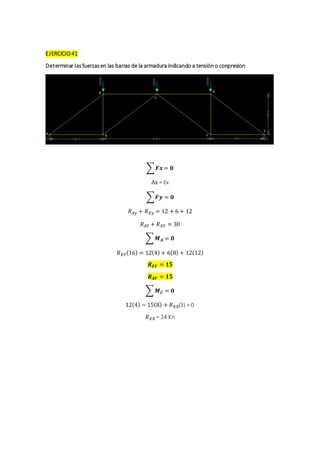
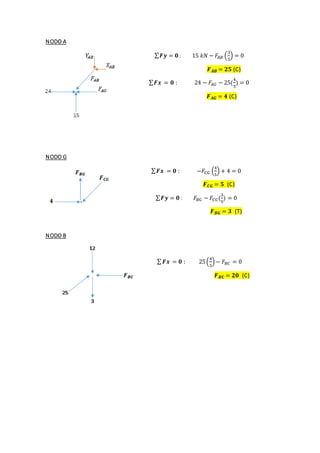
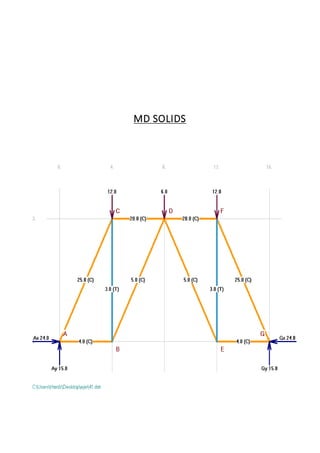
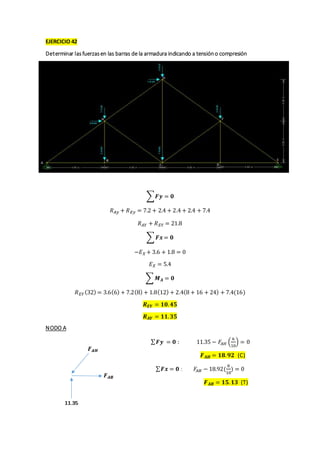
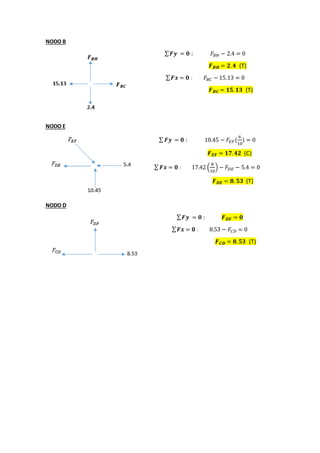
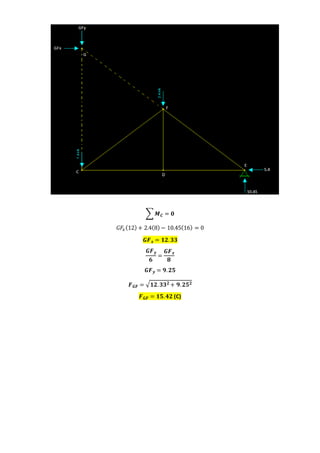
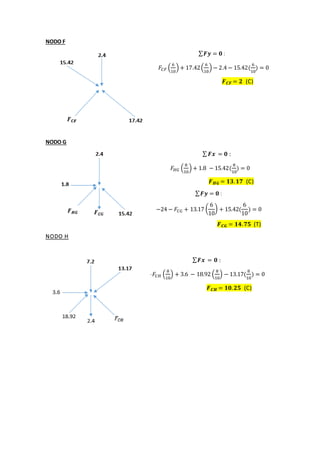
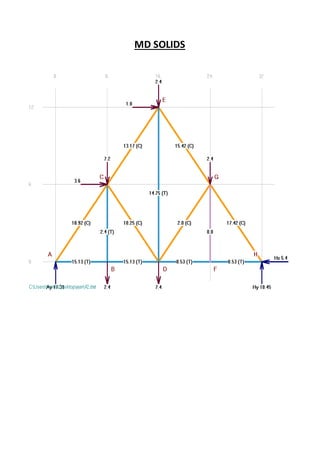
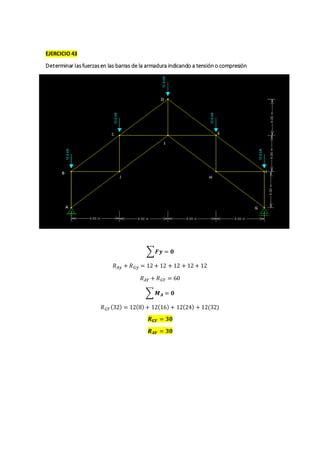
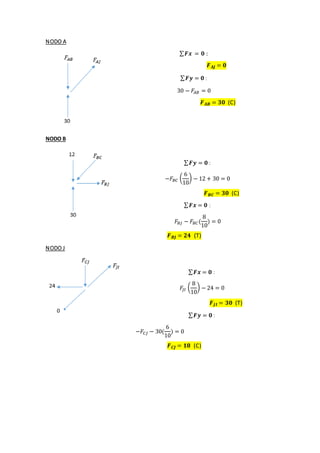
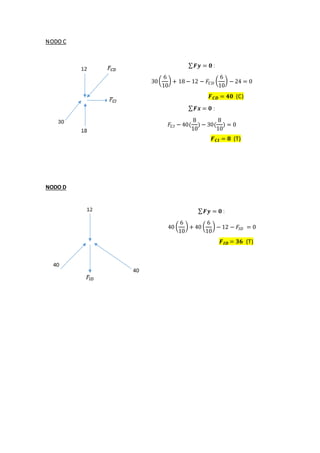
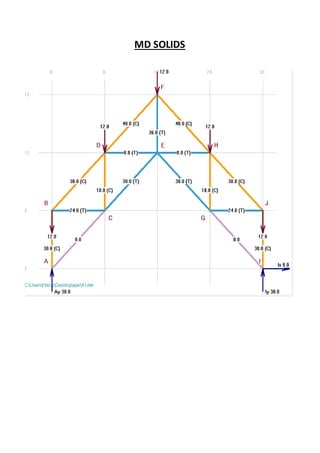
This document contains solutions to structural analysis exercises involving determining forces in reinforcement bars. Exercise 41 involves a frame with nodes A, B, G and calculates the forces in the bars. The forces are: FAB = 25 kN (compression), FAG = 4 kN (compression), FCG = 5 kN (compression), FBG = 3 kN (tension). Exercise 42 involves a similar frame with nodes A, B, D, E, F, G, H and calculates forces such as: FAH = 18.92 kN (compression), FAB = 15.13 kN (tension), FCF = 2 kN (compression). Exercise 43 calculates forces in a frame with nodes A, B,

1. “Año de la consolidación del Mar de Grau”
ANALISIS ESTRUCTURAL I
CAP IV
“ARMADURAS”
“METODOS DE LOS NUDOS”
HARVEY VICTOR JOEL ROA PAIBA
UNP

2. EJERCICIO41
Determinar lasfuerzasen las barras de la armadura indicando a tensióno conpresion
∑ 𝑭𝒙 = 𝟎
Ax = Ex
∑𝑭𝒚 = 𝟎
𝑅 𝐴𝑦 + 𝑅 𝐸𝑦 = 12 + 6 + 12
𝑅 𝐴𝑌 + 𝑅 𝐸𝑌 = 30
∑ 𝑴 𝑨 = 𝟎
𝑅 𝐸𝑌(16) = 12(4) + 6(8) + 12(12)
𝑹 𝑬𝒀 = 𝟏𝟓
𝑹 𝑨𝒀 = 𝟏𝟓
∑ 𝑴 𝑪 = 𝟎
12(4) − 15(8) + 𝑅 𝐸𝑋(3) = 0
𝑅 𝐸𝑋 = 24 Kn

3. NODO A
∑ 𝑭𝒚 = 𝟎 : 15 𝑘𝑁 − 𝐹𝐴𝐵 (
3
5
) = 0
𝑭 𝑨𝑩 = 𝟐𝟓 (C)
∑ 𝑭𝒙 = 𝟎 : 24 − 𝐹𝐴 𝐺 − 25(
4
5
) = 0
𝑭 𝑨𝑮 = 𝟒 (C)
NODO G
∑ 𝑭𝒙 = 𝟎 : −𝐹𝐶𝐺 (
4
5
) + 4 = 0
𝑭 𝑪𝑮 = 𝟓 (C)
∑ 𝑭𝒚 = 𝟎 : 𝐹𝐵𝐺 − 𝐹𝐶𝐺(
3
5
) = 0
𝑭 𝑩𝑮 = 𝟑 (T)
NODO B
∑ 𝑭𝒙 = 𝟎 : 25(
4
5
) − 𝐹𝐵𝐶 = 0
𝑭 𝑩𝑪 = 𝟐𝟎 (C)

4. MD SOLIDS

6. EJERCICIO 42
Determinar lasfuerzasen las barras de la armadura indicando a tensióno compresión
∑𝑭𝒚 = 𝟎
𝑅 𝐴𝑦 + 𝑅 𝐸𝑦 = 7.2 + 2.4 + 2.4 + 2.4 + 7.4
𝑅 𝐴𝑌 + 𝑅 𝐸𝑌 = 21.8
∑ 𝑭𝒙 = 𝟎
−𝐸 𝑋 + 3.6 + 1.8 = 0
𝐸 𝑋 = 5.4
∑ 𝑴 𝑨 = 𝟎
𝑅 𝐸𝑌(32) = 3.6(6) + 7.2(8) + 1.8(12) + 2.4(8 + 16 + 24) + 7.4(16)
𝑹 𝑬𝒀 = 𝟏𝟎. 𝟒𝟓
𝑹 𝑨𝒀 = 𝟏𝟏. 𝟑𝟓
NODO A
∑ 𝑭𝒚 = 𝟎 : 11.35 − 𝐹𝐴𝐻 (
6
10
) = 0
𝑭 𝑨𝑯 = 𝟏𝟖. 𝟗𝟐 (C)
∑ 𝑭𝒙 = 𝟎 : 𝐹𝐴𝐵 − 18.92(
8
10
) = 0
𝑭 𝑨𝑩 = 𝟏𝟓. 𝟏𝟑 (T)

7. NODO B
∑ 𝑭𝒚 = 𝟎 : 𝐹𝐵𝐻 − 2.4 = 0
𝑭 𝑩𝑯 = 𝟐. 𝟒 (T)
∑ 𝑭𝒙 = 𝟎 : 𝐹𝐵𝐶 − 15.13 = 0
𝑭 𝑩𝑪 = 𝟏𝟓. 𝟏𝟑 (T)
NODO E
∑ 𝑭𝒚 = 𝟎 : 10.45 − 𝐹𝐸𝐹(
6
10
) = 0
𝑭 𝑬𝑭 = 𝟏𝟕. 𝟒𝟐 (C)
∑ 𝑭𝒙 = 𝟎 : 17.42 (
8
10
) − 𝐹𝐷𝐸 − 5.4 = 0
𝑭 𝑫𝑬 = 𝟖. 𝟓𝟑 (T)
NODO D
∑ 𝑭𝒚 = 𝟎 : 𝑭 𝑫𝑭 = 𝟎
∑ 𝑭𝒙 = 𝟎 : 8.53 − 𝐹𝐶𝐷 = 0
𝑭 𝑪𝑫 = 𝟖. 𝟓𝟑 (T)

8. ∑ 𝑴 𝑪 = 𝟎
𝐺𝐹𝑥(12) + 2.4(8) − 10.45(16) = 0
𝑮𝑭 𝒙 = 𝟏𝟐. 𝟑𝟑
𝑮𝑭 𝒚
𝟔
=
𝑮𝑭 𝒙
𝟖
𝑮𝑭 𝒚 = 𝟗. 𝟐𝟓
𝑭 𝑮𝑭 = √ 𝟏𝟐. 𝟑𝟑 𝟐 + 𝟗. 𝟐𝟓 𝟐
𝑭 𝑮𝑭 = 𝟏𝟓. 𝟒𝟐 (C)

9. NODO F
∑ 𝑭𝒚 = 𝟎 :
𝐹𝐶𝐹 (
6
10
) + 17.42(
6
10
) − 2.4 − 15.42(
6
10
) = 0
𝑭 𝑪𝑭 = 𝟐 (C)
NODO G
∑ 𝑭𝒙 = 𝟎 :
𝐹𝐻𝐺 (
8
10
) + 1.8 − 15.42(
8
10
) = 0
𝑭 𝑯𝑮 = 𝟏𝟑. 𝟏𝟕 (C)
∑ 𝑭𝒚 = 𝟎 :
−24 − 𝐹𝐶𝐺 + 13.17 (
6
10
) + 15.42(
6
10
) = 0
𝑭 𝑪𝑮 = 𝟏𝟒. 𝟕𝟓 (T)
NODO H
∑ 𝑭𝒙 = 𝟎 :
-𝐹𝐶𝐻 (
8
10
) + 3.6 − 18.92 (
8
10
) − 13.17(
8
10
) = 0
𝑭 𝑪𝑯 = 𝟏𝟎. 𝟐𝟓 (C)

10. MD SOLIDS

11. EJERCICIO 43
Determinar lasfuerzasen las barras de la armadura indicando a tensióno compresión
∑𝑭𝒚 = 𝟎
𝑅 𝐴𝑦 + 𝑅 𝐺𝑦 = 12 + 12 + 12 + 12 + 12
𝑅 𝐴𝑌 + 𝑅 𝐺𝑌 = 60
∑ 𝑴 𝑨 = 𝟎
𝑅 𝐺𝑌(32) = 12(8) + 12(16) + 12(24) + 12(32)
𝑹 𝑮𝒀 = 𝟑𝟎
𝑹 𝑨𝒀 = 𝟑𝟎

12. NODO A
∑ 𝑭𝒙 = 𝟎 :
𝑭 𝑨𝑱 = 𝟎
∑ 𝑭𝒚 = 𝟎 :
30 − 𝐹𝐴 𝐵 = 0
𝑭 𝑨𝑩 = 𝟑𝟎 (C)
NODO B
∑ 𝑭𝒚 = 𝟎 :
−𝐹𝐵𝐶 (
6
10
) − 12 + 30 = 0
𝑭 𝑩𝑪 = 𝟑𝟎 (C)
∑ 𝑭𝒙 = 𝟎 :
𝐹𝐵𝐽 − 𝐹𝐵𝐶(
8
10
) = 0
𝑭 𝑩𝑱 = 𝟐𝟒 (T)
NODO J
∑ 𝑭𝒙 = 𝟎 :
𝐹𝐽𝐼 (
8
10
) − 24 = 0
𝑭 𝑱𝑰 = 𝟑𝟎 (T)
∑ 𝑭𝒚 = 𝟎 :
−𝐹𝐶𝐽 − 30(
6
10
) = 0
𝑭 𝑪𝑱 = 𝟏𝟖 (C)

13. NODO C
∑ 𝑭𝒚 = 𝟎 :
30(
6
10
) + 18 − 12 − 𝐹𝐶𝐷 (
6
10
) − 24 = 0
𝑭 𝑪𝑫 = 𝟒𝟎 (C)
∑ 𝑭𝒙 = 𝟎 :
𝐹𝐶𝐼 − 40(
8
10
) − 30(
8
10
) = 0
𝑭 𝑪𝑰 = 𝟖 (T)
NODO D
∑ 𝑭𝒚 = 𝟎 :
40 (
6
10
) + 40 (
6
10
) − 12 − 𝐹𝐼𝐷 = 0
𝑭 𝑰𝑫 = 𝟑𝟔 (T)

14. MD SOLIDS