Fabrice Kordon, LIP6

1. F.Kordon-UniversitéP.&M.Curie-CC2016
Fabrice.Kordon@lip6.fr
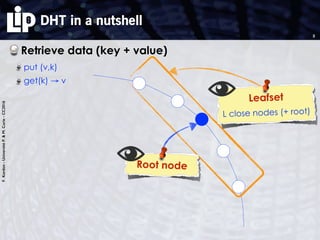
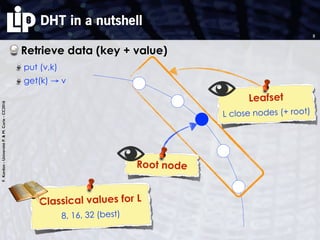
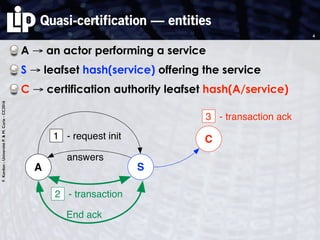
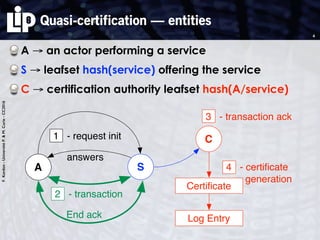
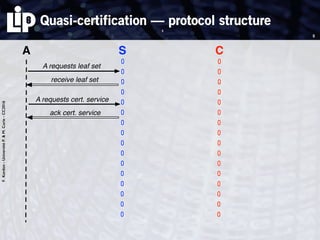
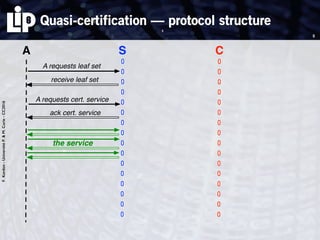
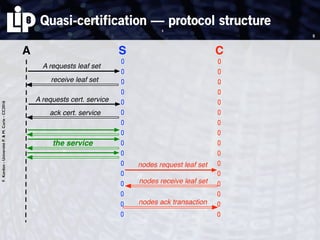
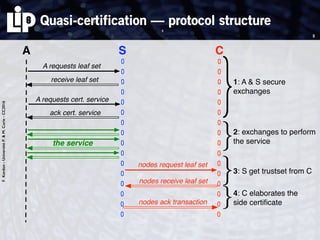
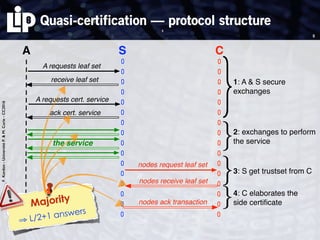
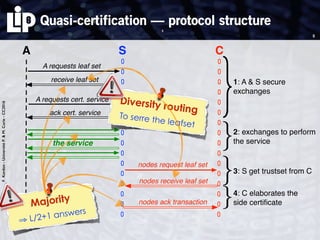
Building and verifying a
quasi-certification entity
over Distributed Hash Tables
Join work with X. Bonnaire, R. Cortes & O. Marin
UPMC (France), UFSM (Chile), NYUS (China)

2. F.Kordon-UniversitéP.&M.Curie-CC2016
Certification, why?
Motivations
Digital filling for tax purpose
‣ Certify that somebody did it before a given deadline
Certified emails
‣ Use emails for legal purposes
Online game refereeing
e-voting, etc.
2

3. F.Kordon-UniversitéP.&M.Curie-CC2016
Certification, why?
Motivations
Digital filling for tax purpose
‣ Certify that somebody did it before a given deadline
Certified emails
‣ Use emails for legal purposes
Online game refereeing
e-voting, etc.
Existing Solutions
Centralized
‣ Public Key Infrastructures (traditional PKI)
‣ Scaling problem/prone to faults/implementation (atomic multicast)
Decentralized
‣ Certification on top of Distributed Hash Tables (DHT)
‣ Rapidly brings Byzantine consensus (for a 100.0% guarantee)
2

4. F.Kordon-UniversitéP.&M.Curie-CC2016
Certification, why?
Motivations
Digital filling for tax purpose
‣ Certify that somebody did it before a given deadline
Certified emails
‣ Use emails for legal purposes
Online game refereeing
e-voting, etc.
Existing Solutions
Centralized
‣ Public Key Infrastructures (traditional PKI)
‣ Scaling problem/prone to faults/implementation (atomic multicast)
Decentralized
‣ Certification on top of Distributed Hash Tables (DHT)
‣ Rapidly brings Byzantine consensus (for a 100.0% guarantee)
2
Objective
(quasi)-certify that a given action hasbeen performed at a certain time
Distributed context (DHT)

5. F.Kordon-UniversitéP.&M.Curie-CC2016
DHT in a nutshell
Retrieve data (key + value)
put (v,k)
get(k) → v
3
Large Scale Distributed System, Design Principles 47

6. F.Kordon-UniversitéP.&M.Curie-CC2016
DHT in a nutshell
Retrieve data (key + value)
put (v,k)
get(k) → v
3
Large Scale Distributed System, Design Principles 47
access in log(n)
Totally decentralized + built)inredundancy for fault tolerance

7. F.Kordon-UniversitéP.&M.Curie-CC2016
DHT in a nutshell
Retrieve data (key + value)
put (v,k)
get(k) → v
3
Root node

8. F.Kordon-UniversitéP.&M.Curie-CC2016
DHT in a nutshell
Retrieve data (key + value)
put (v,k)
get(k) → v
3
Root node
Leafset
L close nodes (+ root)

9. F.Kordon-UniversitéP.&M.Curie-CC2016
DHT in a nutshell
Retrieve data (key + value)
put (v,k)
get(k) → v
3
Root node
Leafset
L close nodes (+ root)
Classical values for L
8, 16, 32 (best)

10. F.Kordon-UniversitéP.&M.Curie-CC2016
Quasi-certification — entities
A → an actor performing a service
4
A

11. F.Kordon-UniversitéP.&M.Curie-CC2016
Quasi-certification — entities
A → an actor performing a service
S → leafset hash(service) offering the service
4
A S
1 - request init
answers

12. F.Kordon-UniversitéP.&M.Curie-CC2016
Quasi-certification — entities
A → an actor performing a service
S → leafset hash(service) offering the service
4
A S
1 - request init
answers
2 - transaction
End ack

13. F.Kordon-UniversitéP.&M.Curie-CC2016
Quasi-certification — entities
A → an actor performing a service
S → leafset hash(service) offering the service
C → certification authority leafset hash(A/service)
4
A S
1 - request init
answers
2 - transaction
End ack
C
3 - transaction ack

14. F.Kordon-UniversitéP.&M.Curie-CC2016
Quasi-certification — entities
A → an actor performing a service
S → leafset hash(service) offering the service
C → certification authority leafset hash(A/service)
4
A S
1 - request init
answers
2 - transaction
End ack
C
3 - transaction ack
Certificate
Log Entry
4 - certificate
generation

15. F.Kordon-UniversitéP.&M.Curie-CC2016
Quasi-certification — protocol structure
5
A S C
5

16. F.Kordon-UniversitéP.&M.Curie-CC2016
Quasi-certification — protocol structure
5
A S C
A requests cert. service
ack cert. service
A requests leaf set
receive leaf set
5

17. F.Kordon-UniversitéP.&M.Curie-CC2016
Quasi-certification — protocol structure
5
A S C
A requests cert. service
ack cert. service
A requests leaf set
receive leaf set
the service
5

18. F.Kordon-UniversitéP.&M.Curie-CC2016
Quasi-certification — protocol structure
5
A S C
A requests cert. service
ack cert. service
A requests leaf set
receive leaf set
the service
nodes ack transaction
nodes request leaf set
nodes receive leaf set
5

19. F.Kordon-UniversitéP.&M.Curie-CC2016
Quasi-certification — protocol structure
5
A S C
A requests cert. service
ack cert. service
A requests leaf set
receive leaf set
the service
nodes ack transaction
nodes request leaf set
nodes receive leaf set
}1: A & S secure
exchanges
}3: S get trustset from C
}2: exchanges to perform
the service
}4: C elaborates the
side certificate
5

20. F.Kordon-UniversitéP.&M.Curie-CC2016
Quasi-certification — protocol structure
5
A S C
A requests cert. service
ack cert. service
A requests leaf set
receive leaf set
the service
nodes ack transaction
nodes request leaf set
nodes receive leaf set
}1: A & S secure
exchanges
}3: S get trustset from C
}2: exchanges to perform
the service
}4: C elaborates the
side certificate
5
Majority
⇒ L/2+1 answers

21. F.Kordon-UniversitéP.&M.Curie-CC2016
Quasi-certification — protocol structure
5
A S C
A requests cert. service
ack cert. service
A requests leaf set
receive leaf set
the service
nodes ack transaction
nodes request leaf set
nodes receive leaf set
}1: A & S secure
exchanges
}3: S get trustset from C
}2: exchanges to perform
the service
}4: C elaborates the
side certificate
5
Diversity routing
To serre the leafset
Majority
⇒ L/2+1 answers

22. F.Kordon-UniversitéP.&M.Curie-CC2016
The verification process
Proof (by any method?)
Proven to be undecidable [FLP 85]
6

23. F.Kordon-UniversitéP.&M.Curie-CC2016
The verification process
Proof (by any method?)
Proven to be undecidable [FLP 85]
So what?
Being pragmatic
Going for «quasi»
6

24. F.Kordon-UniversitéP.&M.Curie-CC2016
The verification process
Proof (by any method?)
Proven to be undecidable [FLP 85]
So what?
Being pragmatic
Going for «quasi»
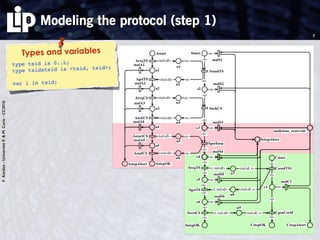
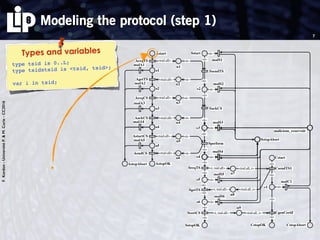
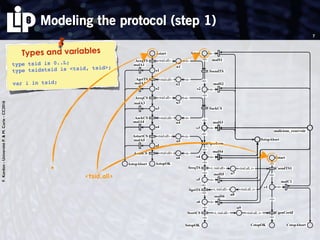
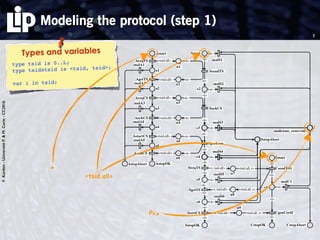
Two steps
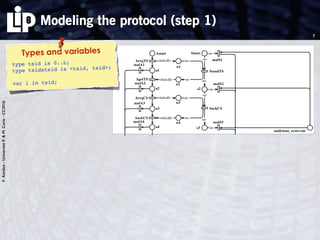
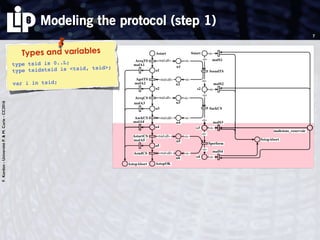
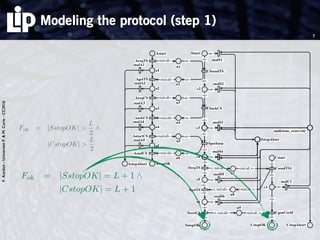
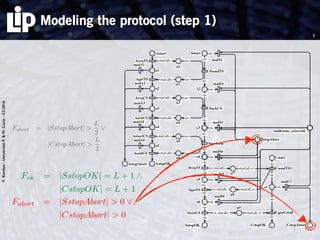
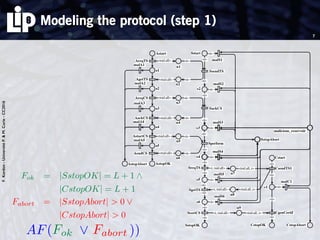
1. modeling the protocol in a perfect world (no error)
Use of Petri nets
2. Probabilistic analysis to evaluate the failure rate
Use of a classical fault model,
building a formula + numeric evaluation
6

25. F.Kordon-UniversitéP.&M.Curie-CC2016
Hypotheses
H1: perfect world
H2: service reduced to 1 interaction
H3: L+1 answer requested instead of L/2+1
‣ Symmetric net with Bags?
Modeling the protocol (step 1)
7

26. F.Kordon-UniversitéP.&M.Curie-CC2016
Modeling the protocol (step 1)
7
Types and variables
type tsid is 0..L;
type tsidxtsid is <tsid, tsid>;
var i in tsid;

27. F.Kordon-UniversitéP.&M.Curie-CC2016
Modeling the protocol (step 1)
7
Types and variables
type tsid is 0..L;
type tsidxtsid is <tsid, tsid>;
var i in tsid;
<i>
<i>
<i>
<i><i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS3
malS2
malS1
malA3
malA4
malA2
malA1
n4
n3
n2
n1
Sstart
s2
s3
SsendTS
SackCS
AackCS
AreqCS
AgetTS
AreqTS
a4
a3
a2
a1
Astart

28. F.Kordon-UniversitéP.&M.Curie-CC2016
Modeling the protocol (step 1)
7
Types and variables
type tsid is 0..L;
type tsidxtsid is <tsid, tsid>;
var i in tsid;
<i>
<i>
<i>
<i><i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS3
malS2
malS1
malA3
malA4
malA2
malA1
n4
n3
n2
n1
Sstart
s2
s3
SsendTS
SackCS
AackCS
AreqCS
AgetTS
AreqTS
a4
a3
a2
a1
Astart
<i>
<i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS4
malS3
malA5
malA4
SstopAbort
AstopAbort
n6
n5
s3
s4
Sperform
AendCS
AstartCS
a5
a4
AstopOK

29. F.Kordon-UniversitéP.&M.Curie-CC2016
Modeling the protocol (step 1)
7
Types and variables
type tsid is 0..L;
type tsidxtsid is <tsid, tsid>;
var i in tsid;
<i>
<i>
<i>
<i><i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS3
malS2
malS1
malA3
malA4
malA2
malA1
n4
n3
n2
n1
Sstart
s2
s3
SsendTS
SackCS
AackCS
AreqCS
AgetTS
AreqTS
a4
a3
a2
a1
Astart
<i>
<i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS4
malS3
malA5
malA4
SstopAbort
AstopAbort
n6
n5
s3
s4
Sperform
AendCS
AstartCS
a5
a4
AstopOK
<i>
<i>
<tsid.all, i>
<i>
<i>
<i>
<i>
<tsid.all, i><i, tsid.all>
<i, tsid.all>
<tsid.all, i><i, tsid.all>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
malicious_reservoir
malC1
malS6
malS5
malS4
CstopAbort
SstopAbort
n9
n8
n7
CgenCertif
CsendTS1
c1
Cstarts4
s5
s6
SstopOK
SreqTS
SgetTS
ScertCS
CstopOK

30. F.Kordon-UniversitéP.&M.Curie-CC2016
Modeling the protocol (step 1)
7
Types and variables
type tsid is 0..L;
type tsidxtsid is <tsid, tsid>;
var i in tsid;
<i>
<i>
<i>
<i><i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS3
malS2
malS1
malA3
malA4
malA2
malA1
n4
n3
n2
n1
Sstart
s2
s3
SsendTS
SackCS
AackCS
AreqCS
AgetTS
AreqTS
a4
a3
a2
a1
Astart
<i>
<i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS4
malS3
malA5
malA4
SstopAbort
AstopAbort
n6
n5
s3
s4
Sperform
AendCS
AstartCS
a5
a4
AstopOK
<i>
<i>
<tsid.all, i>
<i>
<i>
<i>
<i>
<tsid.all, i><i, tsid.all>
<i, tsid.all>
<tsid.all, i><i, tsid.all>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
malicious_reservoir
malC1
malS6
malS5
malS4
CstopAbort
SstopAbort
n9
n8
n7
CgenCertif
CsendTS1
c1
Cstarts4
s5
s6
SstopOK
SreqTS
SgetTS
ScertCS
CstopOK
●

31. F.Kordon-UniversitéP.&M.Curie-CC2016
Modeling the protocol (step 1)
7
Types and variables
type tsid is 0..L;
type tsidxtsid is <tsid, tsid>;
var i in tsid;
<i>
<i>
<i>
<i><i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS3
malS2
malS1
malA3
malA4
malA2
malA1
n4
n3
n2
n1
Sstart
s2
s3
SsendTS
SackCS
AackCS
AreqCS
AgetTS
AreqTS
a4
a3
a2
a1
Astart
<i>
<i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS4
malS3
malA5
malA4
SstopAbort
AstopAbort
n6
n5
s3
s4
Sperform
AendCS
AstartCS
a5
a4
AstopOK
<i>
<i>
<tsid.all, i>
<i>
<i>
<i>
<i>
<tsid.all, i><i, tsid.all>
<i, tsid.all>
<tsid.all, i><i, tsid.all>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
malicious_reservoir
malC1
malS6
malS5
malS4
CstopAbort
SstopAbort
n9
n8
n7
CgenCertif
CsendTS1
c1
Cstarts4
s5
s6
SstopOK
SreqTS
SgetTS
ScertCS
CstopOK
●
<tsid.all>

32. F.Kordon-UniversitéP.&M.Curie-CC2016
Modeling the protocol (step 1)
7
Types and variables
type tsid is 0..L;
type tsidxtsid is <tsid, tsid>;
var i in tsid;
<i>
<i>
<i>
<i><i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS3
malS2
malS1
malA3
malA4
malA2
malA1
n4
n3
n2
n1
Sstart
s2
s3
SsendTS
SackCS
AackCS
AreqCS
AgetTS
AreqTS
a4
a3
a2
a1
Astart
<i>
<i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS4
malS3
malA5
malA4
SstopAbort
AstopAbort
n6
n5
s3
s4
Sperform
AendCS
AstartCS
a5
a4
AstopOK
<i>
<i>
<tsid.all, i>
<i>
<i>
<i>
<i>
<tsid.all, i><i, tsid.all>
<i, tsid.all>
<tsid.all, i><i, tsid.all>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
malicious_reservoir
malC1
malS6
malS5
malS4
CstopAbort
SstopAbort
n9
n8
n7
CgenCertif
CsendTS1
c1
Cstarts4
s5
s6
SstopOK
SreqTS
SgetTS
ScertCS
CstopOK
●
<tsid.all>
Px●

33. F.Kordon-UniversitéP.&M.Curie-CC2016
Modeling the protocol (step 1)
7
<i>
<i>
<i>
<i><i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS3
malS2
malS1
malA3
malA4
malA2
malA1
n4
n3
n2
n1
Sstart
s2
s3
SsendTS
SackCS
AackCS
AreqCS
AgetTS
AreqTS
a4
a3
a2
a1
Astart
<i>
<i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS4
malS3
malA5
malA4
SstopAbort
AstopAbort
n6
n5
s3
s4
Sperform
AendCS
AstartCS
a5
a4
AstopOK
<i>
<i>
<tsid.all, i>
<i>
<i>
<i>
<i>
<tsid.all, i><i, tsid.all>
<i, tsid.all>
<tsid.all, i><i, tsid.all>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
malicious_reservoir
malC1
malS6
malS5
malS4
CstopAbort
SstopAbort
n9
n8
n7
CgenCertif
CsendTS1
c1
Cstarts4
s5
s6
SstopOK
SreqTS
SgetTS
ScertCS
CstopOK
Fok = |SstopOK| = L + 1
|CstopOK| = L + 1
Fok = |SstopOK| >
L
2
^
|CstopOK| >
L
2

34. F.Kordon-UniversitéP.&M.Curie-CC2016
Modeling the protocol (step 1)
7
<i>
<i>
<i>
<i><i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS3
malS2
malS1
malA3
malA4
malA2
malA1
n4
n3
n2
n1
Sstart
s2
s3
SsendTS
SackCS
AackCS
AreqCS
AgetTS
AreqTS
a4
a3
a2
a1
Astart
<i>
<i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS4
malS3
malA5
malA4
SstopAbort
AstopAbort
n6
n5
s3
s4
Sperform
AendCS
AstartCS
a5
a4
AstopOK
<i>
<i>
<tsid.all, i>
<i>
<i>
<i>
<i>
<tsid.all, i><i, tsid.all>
<i, tsid.all>
<tsid.all, i><i, tsid.all>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
malicious_reservoir
malC1
malS6
malS5
malS4
CstopAbort
SstopAbort
n9
n8
n7
CgenCertif
CsendTS1
c1
Cstarts4
s5
s6
SstopOK
SreqTS
SgetTS
ScertCS
CstopOK
Fok = |SstopOK| = L + 1
|CstopOK| = L + 1
Fabort = |SstopAbort| > 0
|CstopAbort| > 0
Fabort = |SstopAbort| >
L
2
_
|CstopAbort| >
L
2

35. F.Kordon-UniversitéP.&M.Curie-CC2016
Modeling the protocol (step 1)
7
<i>
<i>
<i>
<i><i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS3
malS2
malS1
malA3
malA4
malA2
malA1
n4
n3
n2
n1
Sstart
s2
s3
SsendTS
SackCS
AackCS
AreqCS
AgetTS
AreqTS
a4
a3
a2
a1
Astart
<i>
<i>
<i>
<i>
<tsid.all> <i>
<tsid.all>
<i>
<i>
malicious_reservoir
malS4
malS3
malA5
malA4
SstopAbort
AstopAbort
n6
n5
s3
s4
Sperform
AendCS
AstartCS
a5
a4
AstopOK
<i>
<i>
<tsid.all, i>
<i>
<i>
<i>
<i>
<tsid.all, i><i, tsid.all>
<i, tsid.all>
<tsid.all, i><i, tsid.all>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
<i>
malicious_reservoir
malC1
malS6
malS5
malS4
CstopAbort
SstopAbort
n9
n8
n7
CgenCertif
CsendTS1
c1
Cstarts4
s5
s6
SstopOK
SreqTS
SgetTS
ScertCS
CstopOK
FabortFokAF( _ ))
Fok = |SstopOK| = L + 1
|CstopOK| = L + 1
Fabort = |SstopAbort| > 0
|CstopAbort| > 0

36. F.Kordon-UniversitéP.&M.Curie-CC2016
Verifying the perfect world
About the complexity of the state space
Roughly 10L
states
1 state= 13 int + 17 multistep ⇒ memory problem to check for L=32
8
1E+02
1E+04
1E+06
1E+08
1E+10
1E+12
1E+14
1E+16
1E+18
1E+20
1E+22
2 4 6 8 10 12 14 16 18 20 22
Numberofstates
Leaf set size
Size of the state space
Reachability graph
Symb. reach. graph

37. F.Kordon-UniversitéP.&M.Curie-CC2016
Verifying the perfect world
About the complexity of the state space
Roughly 10L
states
1 state= 13 int + 17 multistep ⇒ memory problem to check for L=32
GreatSPN (use of symmetries)
L=24 fails after 11h45mn of CPU (costly canonisation function)
‣ Implementation limit = size of a hash table
8
1E+02
1E+04
1E+06
1E+08
1E+10
1E+12
1E+14
1E+16
1E+18
1E+20
1E+22
2 4 6 8 10 12 14 16 18 20 22
Numberofstates
Leaf set size
Size of the state space
Reachability graph
Symb. reach. graph

38. F.Kordon-UniversitéP.&M.Curie-CC2016
Verifying the perfect world
About the complexity of the state space
Roughly 10L
states
1 state= 13 int + 17 multistep ⇒ memory problem to check for L=32
GreatSPN (use of symmetries)
L=24 fails after 11h45mn of CPU (costly canonisation function)
‣ Implementation limit = size of a hash table
PNXDD (decision diagrams + variable ordering)
Unfolding to P/T nets
L=10 fails after 3h20mn (memory overflow > 16GB)
8

39. F.Kordon-UniversitéP.&M.Curie-CC2016
Verifying the perfect world
About the complexity of the state space
Roughly 10L
states
1 state= 13 int + 17 multistep ⇒ memory problem to check for L=32
GreatSPN (use of symmetries)
L=24 fails after 11h45mn of CPU (costly canonisation function)
‣ Implementation limit = size of a hash table
PNXDD (decision diagrams + variable ordering)
Unfolding to P/T nets
L=10 fails after 3h20mn (memory overflow > 16GB)
ITS-Tools (hierarchical decision diagrams)
Completed for L=32 in less than one minute
‣ Handling of symmetries in the system by means of a dedicated encoding
8

40. F.Kordon-UniversitéP.&M.Curie-CC2016
Verifying the perfect world
8
http://cosyverif.org

41. F.Kordon-UniversitéP.&M.Curie-CC2016
Probabilistic analysis (step 2)
Classical approach of the domain
Based on p, probability of node failure
‣ Hypotheses required
‣ Diversity routing to avoid coalitions
9

42. F.Kordon-UniversitéP.&M.Curie-CC2016
Probabilistic analysis (step 2)
Classical approach of the domain
Based on p, probability of node failure
‣ Hypotheses required
‣ Diversity routing to avoid coalitions
Origin of problems
Source 1 → failure of the protocol
‣ No answer to A + no ack to A
‣ Interactions between A, S (leafset)
Source 2 → inappropriate certificate
‣ Lost of a certificate (inconsistency)
‣ Interactions between S (leafset) and C (leafset)
9

43. F.Kordon-UniversitéP.&M.Curie-CC2016
Probabilistic analysis (step 2)
Classical approach of the domain
Based on p, probability of node failure
‣ Hypotheses required
‣ Diversity routing to avoid coalitions
Origin of problems
Source 1 → failure of the protocol
‣ No answer to A + no ack to A
‣ Interactions between A, S (leafset)
Source 2 → inappropriate certificate
‣ Lost of a certificate (inconsistency)
‣ Interactions between S (leafset) and C (leafset)
9
Numerical applicationsp = 0.3 («untrusted») P = 0.05 («trusted»)

44. F.Kordon-UniversitéP.&M.Curie-CC2016
Formulas and experimental values
Protocol failure
More that L/2 nodes are malicious
The formula:
10
PL+1
i=1
L+1
i pi
(1 p)L+1 i
PL
2
i=1
L+1
i pi
(1 p)L+1 i
at most L+1
malicious nodes
at most L/2
malicious nodes
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠

45. F.Kordon-UniversitéP.&M.Curie-CC2016
Formulas and experimental values
Protocol failure
More that L/2 nodes are malicious
The formula:
10
PL+1
i=1
L+1
i pi
(1 p)L+1 i
PL
2
i=1
L+1
i pi
(1 p)L+1 i
at most L+1
malicious nodes
at most L/2
malicious nodes
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
1.16e-43
1 4 8 12 16 20 24 28
Amount of faulty nodes [k]
CORPS 5% of faulty nodes
FIGURE 5.1. Probability to have more than k malicinodes
L DHT - p = 0.3 CORPS - p = 0.05
8 0.188 6.64 ⇥ 10 5
16 0.079 6.57 ⇥ 10 8
32 0.016 8.24 ⇥ 10 14
TABLE 3. Probability of failure of the transaction betweA and S
From equation 5.6 we can deduce the probability thaS won’t respond to the RequestInit or won’t send thfinal ACKs as
PAS = (1 P>L/2)P>|L|/2 + P>|L|/2
PAS = 2P>|L|/2 P 2
>|L|/2
(5.7
Table 3 shows the probability of failure between Aand S, for a trustset size of |L| = {8, 16, 32} nodes, andcompares a quasi CA built directly above the DHT toone built above CORPS. We consider that the worstcase is when the malicious nodes represent 30% of theDHT nodes. In

46. F.Kordon-UniversitéP.&M.Curie-CC2016
Formulas and experimental values
Protocol failure
More that L/2 nodes are malicious
The formula:
Inappropriate certificate generation
Two parts
‣ Existence of more L/2 malicious nodes
‣ Unable to retrieve at least L/2 + 1 identical answers
The formula (combines problems between S and C)
10
PL+1
i=1
L+1
i pi
(1 p)L+1 i
PL
2
i=1
L+1
i pi
(1 p)L+1 i
at most L+1
malicious nodes
at most L/2
malicious nodes
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
1.16e-43
1 4 8 12 16 20 24 28
Amount of faulty nodes [k]
CORPS 5% of faulty nodes
FIGURE 5.1. Probability to have more than k malicinodes
L DHT - p = 0.3 CORPS - p = 0.05
8 0.188 6.64 ⇥ 10 5
16 0.079 6.57 ⇥ 10 8
32 0.016 8.24 ⇥ 10 14
TABLE 3. Probability of failure of the transaction betweA and S
From equation 5.6 we can deduce the probability thaS won’t respond to the RequestInit or won’t send thfinal ACKs as
PAS = (1 P>L/2)P>|L|/2 + P>|L|/2
PAS = 2P>|L|/2 P 2
>|L|/2
(5.7
Table 3 shows the probability of failure between Aand S, for a trustset size of |L| = {8, 16, 32} nodes, andcompares a quasi CA built directly above the DHT toone built above CORPS. We consider that the worstcase is when the malicious nodes represent 30% of theDHT nodes. In
1 (1 P> L
2
)2

47. F.Kordon-UniversitéP.&M.Curie-CC2016
Formulas and experimental values
Protocol failure
More that L/2 nodes are malicious
The formula:
Inappropriate certificate generation
Two parts
‣ Existence of more L/2 malicious nodes
‣ Unable to retrieve at least L/2 + 1 identical answers
The formula (combines problems between S and C)
10
PL+1
i=1
L+1
i pi
(1 p)L+1 i
PL
2
i=1
L+1
i pi
(1 p)L+1 i
at most L+1
malicious nodes
at most L/2
malicious nodes
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
1.16e-43
1 4 8 12 16 20 24 28
Amount of faulty nodes [k]
CORPS 5% of faulty nodes
FIGURE 5.1. Probability to have more than k malicinodes
L DHT - p = 0.3 CORPS - p = 0.05
8 0.188 6.64 ⇥ 10 5
16 0.079 6.57 ⇥ 10 8
32 0.016 8.24 ⇥ 10 14
TABLE 3. Probability of failure of the transaction betweA and S
From equation 5.6 we can deduce the probability thaS won’t respond to the RequestInit or won’t send thfinal ACKs as
PAS = (1 P>L/2)P>|L|/2 + P>|L|/2
PAS = 2P>|L|/2 P 2
>|L|/2
(5.7
Table 3 shows the probability of failure between Aand S, for a trustset size of |L| = {8, 16, 32} nodes, andcompares a quasi CA built directly above the DHT toone built above CORPS. We consider that the worstcase is when the malicious nodes represent 30% of theDHT nodes. In
1
⇣
1
PL+1
i=1
L+1
i pi
(1 p)L+1 i
+
PL
2
i=1
L+1
i pi
(1 p)L+1 i
⌘2
1 (1 P> L
2
)2

48. F.Kordon-UniversitéP.&M.Curie-CC2016
Formulas and experimental values
Protocol failure
More that L/2 nodes are malicious
The formula:
Inappropriate certificate generation
Two parts
‣ Existence of more L/2 malicious nodes
‣ Unable to retrieve at least L/2 + 1 identical answers
The formula (combines problems between S and C)
10
PL+1
i=1
L+1
i pi
(1 p)L+1 i
PL
2
i=1
L+1
i pi
(1 p)L+1 i
at most L+1
malicious nodes
at most L/2
malicious nodes
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
1.16e-43
1 4 8 12 16 20 24 28
Amount of faulty nodes [k]
CORPS 5% of faulty nodes
FIGURE 5.1. Probability to have more than k malicinodes
L DHT - p = 0.3 CORPS - p = 0.05
8 0.188 6.64 ⇥ 10 5
16 0.079 6.57 ⇥ 10 8
32 0.016 8.24 ⇥ 10 14
TABLE 3. Probability of failure of the transaction betweA and S
From equation 5.6 we can deduce the probability thaS won’t respond to the RequestInit or won’t send thfinal ACKs as
PAS = (1 P>L/2)P>|L|/2 + P>|L|/2
PAS = 2P>|L|/2 P 2
>|L|/2
(5.7
Table 3 shows the probability of failure between Aand S, for a trustset size of |L| = {8, 16, 32} nodes, andcompares a quasi CA built directly above the DHT toone built above CORPS. We consider that the worstcase is when the malicious nodes represent 30% of theDHT nodes. In
1
⇣
1
PL+1
i=1
L+1
i pi
(1 p)L+1 i
+
PL
2
i=1
L+1
i pi
(1 p)L+1 i
⌘2
1 (1 P> L
2
)2
L DHT - p = 0.3 CORPS - p = 0.058 0.216 4.97 ⇥ 10 4
16 0.075 3.50 ⇥ 10 8
32 0.014 4.24 ⇥ 10 13

49. F.Kordon-UniversitéP.&M.Curie-CC2016
Conclusion
Quasi-certification entity (elaboration + verification)
Low probability of failure + Good message complexity (not discussed)
11

50. F.Kordon-UniversitéP.&M.Curie-CC2016
Conclusion
Quasi-certification entity (elaboration + verification)
Low probability of failure + Good message complexity (not discussed)
11
Application to digital tax filling in France
‣ 36.5 M revenues declarations (in 2012)
‣ a wrong tax certificate every 5132 years
‣ lost of a tax certificate every 997 years

51. F.Kordon-UniversitéP.&M.Curie-CC2016
Conclusion
Quasi-certification entity (elaboration + verification)
Low probability of failure + Good message complexity (not discussed)
3 years of work (details recently fixed)
‣ Work partially published in TrustCom’2013
‣ Without formal proof (there was yet glitches details with hypotheses)
11
Application to digital tax filling in France
‣ 36.5 M revenues declarations (in 2012)
‣ a wrong tax certificate every 5132 years
‣ lost of a tax certificate every 997 years

52. F.Kordon-UniversitéP.&M.Curie-CC2016
Conclusion
Quasi-certification entity (elaboration + verification)
Low probability of failure + Good message complexity (not discussed)
3 years of work (details recently fixed)
‣ Work partially published in TrustCom’2013
‣ Without formal proof (there was yet glitches details with hypotheses)
Realistic problem with applicability to e-government
Probably numerous applications in the future
The model is now a metric for the Model Checking Contest
Potential applicability for Symmetric Nets with Bags
‣ Excellent playground for this type of problems
11
Application to digital tax filling in France
‣ 36.5 M revenues declarations (in 2012)
‣ a wrong tax certificate every 5132 years
‣ lost of a tax certificate every 997 years