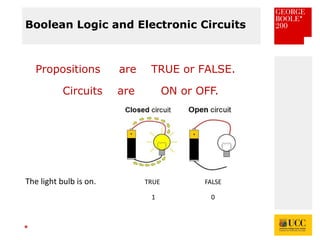
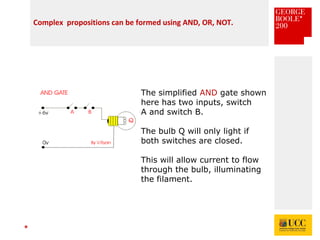
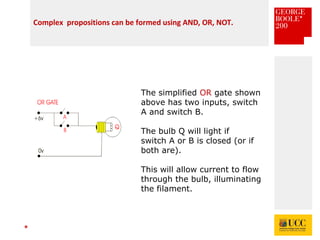
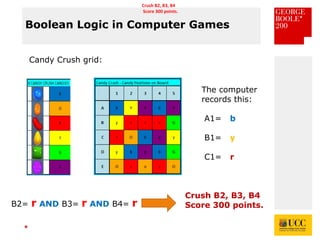
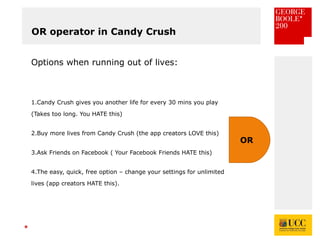
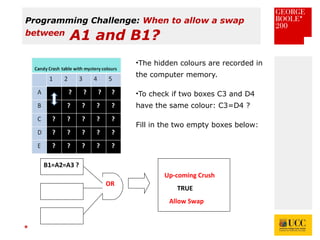
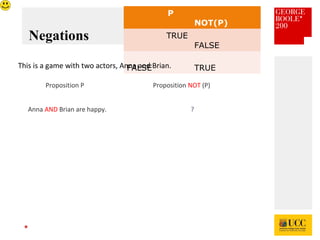
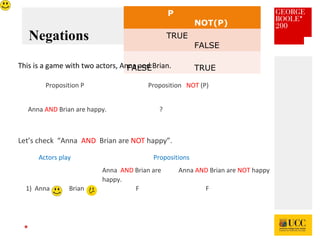
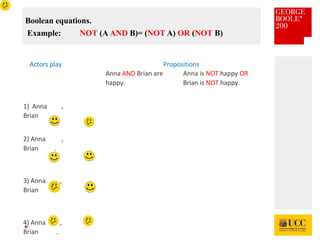
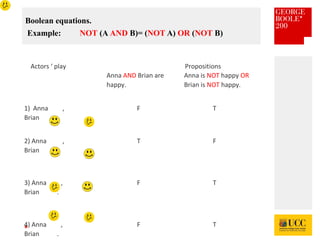
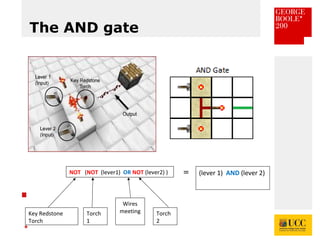
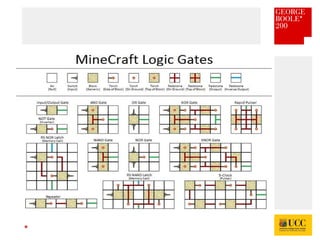
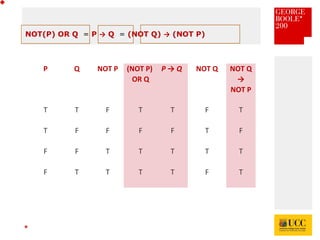
The document celebrates the bicentenary of George Boole, the inventor of Boolean logic, emphasizing its significance in modern computing. It outlines Boole's life, education, and contributions to mathematics, alongside the later application of his ideas by Claude Shannon in circuit theory. Additionally, it explains Boolean logic's principles and its practical applications in computer games and everyday problem-solving.

1. *genius
*1815-2015
CELEBRATING GEORGE BOOLE’S BICENTENARY
University College Cork Ireland

2. *
UCC Brings Boole2School

3. *
Who was George Boole?
Born 1815 in the English
cathedral city of Lincoln.
Inventor of Boolean Logic,
which is the basis of modern
digital computers.
First Professor of Mathematics
at Queen's College Cork (now
UCC).

4. *
George Boole the Teacher
 In 1832, at age 16, he
became the main provider for
his family.
 He took work as an assistant
teacher.
 In 1834, aged 18, he opened
his own school in Free School
Lane, Lincoln.
 In 1838, he took charge of
Waddington Academy.
In 1840 he opened a boarding school at Pottergate in
Lincoln to further improve his family’s financial security.

5. *
George Boole
the Mathematician
• From 1831, Boole began an
ambitious programme of self-
education in mathematics.
• In November 1844 was awarded a
Gold Medal in Mathematics by the
Royal Society for his paper On a
General Method of Analysis.
• Boole became the first
Mathematics professor at UCC in
1849.
• He wrote ‘An Investigation of the
Laws of Thought’ in 1854.
1815-1864

6. *
George Boole and Claude Shannon: Modern Circuit Theory
 Boole’s ideas did not grow to their full
potential until 70 years after his
death in 1864
 US engineer Claude Shannon saw the
potential of Boolean logic for
simplifying design of telephone
switching circuits.
 This led directly to the development
of the modern computer.

7. *
What is Logic?
Logic is concerned with deciding whether
arguments are correct or not.
Example of an argument:
Mary is human.
Assumptions
Humans are mortal.
Therefore Mary is mortal. Conclusion

8. *
Boolean Logic.
•Boolean Logic works with propositions.
•Propositions are either TRUE or FALSE.
TRUE = 1 FALSE = 0
Decide which of these are propositions:
(1) What time is it?
(2) John’s T-shirt is red.
(3) This statement you’re reading just
now is false.

9. *
Boolean Logic and Electronic Circuits
Circuits are ON or OFF.
The light bulb is on. TRUE FALSE
1 0
Propositions are TRUE or FALSE.

10. *
Complex propositions can be formed using AND, OR, NOT.
The simplified AND gate shown
here has two inputs, switch
A and switch B.
The bulb Q will only light if
both switches are closed.
This will allow current to flow
through the bulb, illuminating
the filament.

11. *
Complex propositions can be formed using AND, OR, NOT.
The simplified OR gate shown
above has two inputs, switch
A and switch B.
The bulb Q will light if
switch A or B is closed (or if
both are).
This will allow current to flow
through the bulb, illuminating
the filament.

12. *
Boolean Searches on the Web
•You can search for Swift AND Dreams
•You can search for Swift OR Dreams
•You can search for Swift NOT Dreams
Try it out

13. *
Boolean Logic in Computer Games
Candy Crush
You must swap two pieces of candy to get three
candies of the same colour lined up.

14. *
Boolean Logic in Computer Games
The computer
records this:
A1= b
B1= y
C1= r
Candy Crush grid:
B2= r AND B3= r AND B4= r
Crush B2, B3, B4
Score 300 points.
Crush B2, B3, B4
Score 300 points.

15. *
OR operator in Candy Crush
Options when running out of lives:
1.Candy Crush gives you another life for every 30 mins you play
(Takes too long. You HATE this)
2.Buy more lives from Candy Crush (the app creators LOVE this)
3.Ask Friends on Facebook ( Your Facebook Friends HATE this)
4.The easy, quick, free option – change your settings for unlimited
lives (app creators HATE this).
OR

16. *
Programming Challenge: When to allow a swap
between
A1 and B1?
•The hidden colours are recorded in
the computer memory.
•To check if two boxes C3 and D4
have the same colour: C3=D4 ?
Fill in the two empty boxes below:
B1=A2=A3 ?
OR
Up-coming Crush
TRUE
Allow Swap

17. *
Negations
P
NOT(P)
TRUE
FALSE
FALSE TRUEThis is a game with two actors, Anna and Brian.
Proposition P Proposition NOT (P)
Anna AND Brian are happy. ?

18. *
Negations
Let’s check “Anna AND Brian are NOT happy”.
P
NOT(P)
TRUE
FALSE
FALSE TRUEThis is a game with two actors, Anna and Brian.
Actors play Propositions
Anna AND Brian are
happy.
Anna AND Brian are NOT happy
1) Anna , Brian . F F
Proposition P Proposition NOT (P)
Anna AND Brian are happy. ?

19. *
Boolean equations.
Example: NOT (A AND B)= (NOT A) OR (NOT B)
Actors play Propositions
Anna AND Brian are
happy.
Anna is NOT happy OR
Brian is NOT happy.
1) Anna ,
Brian .
2) Anna ,
Brian .
3) Anna ,
Brian .
4) Anna ,
Brian .

20. *
Boolean equations.
Example: NOT (A AND B)= (NOT A) OR (NOT B)
Actors ‘ play Propositions
Anna AND Brian are
happy.
Anna is NOT happy OR
Brian is NOT happy.
1) Anna ,
Brian .
F T
2) Anna ,
Brian .
T F
3) Anna ,
Brian .
F T
4) Anna ,
Brian .
F T

21. *
Logic in Computer Games
Minecraft
Mainly a construction game.
The most interesting building
material is the Redstone dust,
which can transmit Power
Power can travel through
circuits and activate devices,
like say a lamp or an elevator.
Here is the simplest Redstone
circuit:

22. *
The NOT and OR gates
OR gate
Lever 1 input Lever 2 input Output
TRUE TRUE TRUE
TRUE FALSE TRUE
FALSE TRUE TRUE
FALSE FALSE FALSE
INPUT:
current into torch
OUTPUT:
current from torch
TRUE FALSE
FALSE TRUE

23. *
The AND gate
NOT (NOT (lever1) OR NOT (lever2) )
Key Redstone
Torch
Torch
1
Torch
2
Wires
meeting
(lever 1) AND (lever 2)=

24. *

25. *
NOT
(IF…THEN)
Correct?
One day the famous scientist Dr Doom makes a public
announcement:
“IF there is an earthquake tomorrow,
THEN this entire building will fall down.”
The next day, everybody talks about how Dr Doom
was so wrong.
What happened?

26. *
NOT
(IF…THEN)
Correct?
The President of the school Bridge club is very good at cheating.
Just before the last game, Justine told the president
“IF you cheat, THEN you’ll have to quit!”
The president does his best – and succeeds – in proving Justine wrong.
a) In your opinion, what did the President do to prove Justine wrong?
b) The club members decided to send a last warning to their President.
They staged a protest called “IF you cheat, THEN you quit!”
Find a way to chant this message which is shorter, catchier, and doesn’t use
IF…THEN but rather some of the Boolean operators like AND, OR and NOT.
Hint: It is the opposite statement to what the President did.

27. *
NOT
(IF…THEN)
The President of the school Bridge club is very good at cheating.
Just before the last game, Justine told the president
“IF you cheat, THEN you’ll have to quit!”
The President does his best – and succeeds – in proving Justine wrong.
Justine: What the President
did to prove Justine
wrong:
Club members
warn the
President:
English: “IF you Cheat THEN
you Quit!”
Boolean
Logic:
IF C THEN Q

28. *
NOT(P) OR Q = P → Q = (NOT Q) → (NOT P)
P Q NOT P (NOT P)
OR Q
P → Q NOT Q NOT Q
→
NOT P
T T
T F
F F
F T

29. *
NOT(P) OR Q = P → Q = (NOT Q) → (NOT P)
P Q NOT P (NOT P)
OR Q
P → Q NOT Q NOT Q
→
NOT P
T T F T T F T
T F F F F T F
F F T T T T T
F T T T T F T

30. *
Lesson content
Maths Circles Ireland:
http://mathscircles.ie/