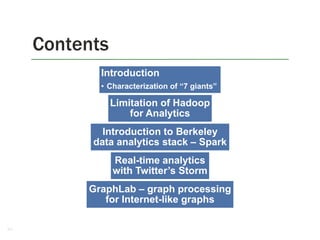
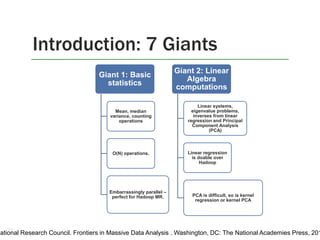
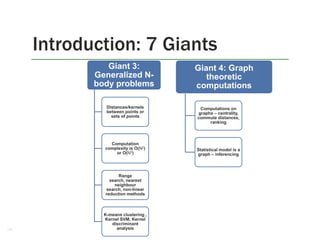
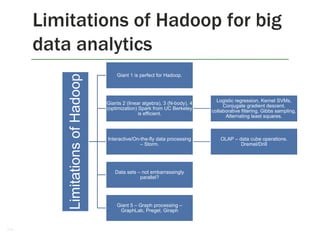
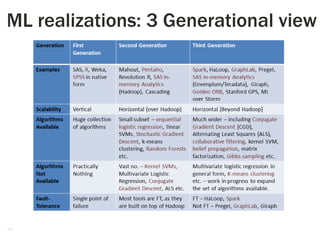
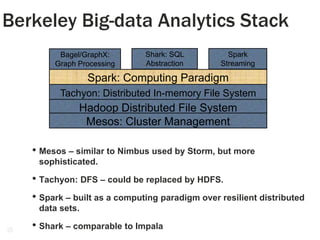
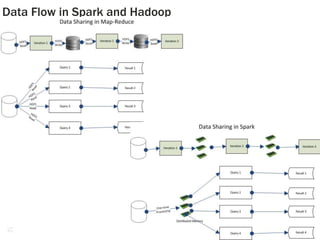
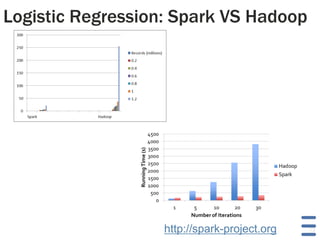
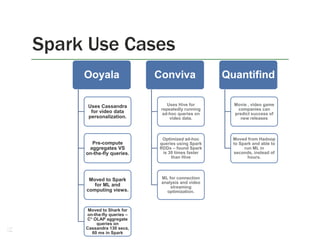
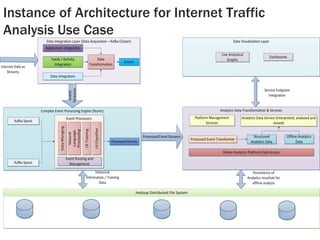
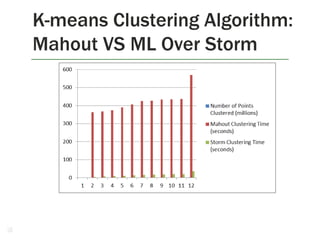
1. The document discusses the limitations of Hadoop for advanced analytics tasks beyond basic statistics like mean and variance. 2. It introduces several distributed data analytics platforms like Spark, Storm, and GraphLab that can perform tasks like linear algebra, graph processing, and iterative machine learning algorithms more efficiently than Hadoop. 3. Specific use cases from companies that moved from Hadoop to these platforms are discussed, where they saw significantly faster performance for tasks like logistic regression, collaborative filtering, and k-means clustering.

1. 1
Big Data Analytics beyond
Hadoop
Dr. Vijay Srinivas Agneeswaran,
Director and Head, Big-data R&D,
Innovation Labs, Impetus

2. Contents
2
Introduction
• Characterization of “7 giants”
Limitation of Hadoop
for Analytics
Introduction to Berkeley
data analytics stack – Spark
Real-time analytics
with Twitter’s Storm
GraphLab – graph processing
for Internet-like graphs

3. Introduction: 7 Giants
3
National Research Council. Frontiers in Massive Data Analysis . Washington, DC: The National Academies Press, 201
Giant 1: Basic
statistics
Mean, median
variance, counting
operations
O(N) operations.
Embarrassingly parallel –
perfect for Hadoop MR.
Giant 2: Linear
Algebra
computations
Linear systems,
eigenvalue problems,
inverses from linear
regression and Principal
Component Analysis
(PCA)
Linear regression
is doable over
Hadoop
PCA is difficult, so is kernel
regression or kernel PCA

4. Introduction: 7 Giants
4
Giant 3:
Generalized N-
body problems
Distances/kernels
between points or
sets of points
Computation
complexity is O(N2)
or O(N3)
Range
search, nearest
neighbour
search, non-linear
reduction methods
K-means clustering ,
Kernel SVM, Kernel
discriminant
analysis
Giant 4: Graph
theoretic
computations
Computations on
graphs – centrality,
commute distances,
ranking
Statistical model is a
graph – inferencing

5. Introduction: 7 Giants
5
[AA11] Alekh Agarwal, Olivier Chapelle, Miroslav Dudík, John Langford: A Reliable Effective
Terascale Linear Learning System. CoRR abs/1110.4198(2011).
Giant 5:
Optimization
problems
Objective/loss/cost/energy
function
maximizing/minimizing
Stochastic
approaches
Linear/quadratic
programmingConjugate gradient
descent
All-reduce
paradigm is
required [AA11]

6. Introduction: 7 Giants
6
Giant 6:
Integration
problems
Bayesian inference or
random effects
models
Quadrature
approaches for low
dimension integration
Markov Chain Monte
Carlo (MCMC) for
high dimension
integration [CA03]
Giant 7:
Alignment
problems
Image deduplication,
catalog cross
matching, multiple
sequence alignments
Linear algebra
Dynamic
programming/Hidden
Markov Models

7. Limitations of Hadoop for big
data analytics
7
LimitationsofHadoop Giant 1 is perfect for Hadoop.
Giants 2 (linear algebra), 3 (N-body), 4
(optimization) Spark from UC Berkeley
is efficient.
Logistic regression, Kernel SVMs,
Conjugate gradient descent,
collaborative filtering, Gibbs sampling,
Alternating least squares.
Interactive/On-the-fly data processing
– Storm.
OLAP – data cube operations.
Dremel/Drill
Data sets – not embarrassingly
parallel?
Giant 5 – Graph processing –
GraphLab, Pregel, Giraph

8. 8
ML realizations: 3 Generational view

9. Iterative ML Algorithms
 What are iterative algorithms?
 Those that need communication among the computing entities
 Examples – neural networks, PageRank algorithms, network traffic analysis
 Conjugate gradient descent
 Commonly used to solve systems of linear equations
 [CB09] tried implementing CG on dense matrices
 DAXPY – Multiplies vector x by constant a and adds y.
 DDOT – Dot product of 2 vectors
 MatVec – Multiply matrix by vector, produce a vector.
 1 MR per primitive – 6 MRs per CG iteration, hundreds of MRs per CG
computation, leading to 10 of GBs of communication even for small
matrices.
 Other iterative algorithms – fast fourier transform, block tridiagonal
[CB09] C. Bunch, B. Drawert, M. Norman, Mapscale: a cloud environment for scientific
computing, Technical Report, University of California, Computer Science Department, 2009.

10. 10
Berkeley Big-data Analytics Stack
Hadoop Distributed File System
Tachyon: Distributed In-memory File System
Spark: Computing Paradigm
Bagel/GraphX:
Graph Processing
• Mesos – similar to Nimbus used by Storm, but more
sophisticated.
• Tachyon: DFS – could be replaced by HDFS.
• Spark – built as a computing paradigm over resilient distributed
data sets.
• Shark – comparable to Impala
Shark: SQL
Abstraction
Spark
Streaming
Mesos: Cluster Management

11. Spark: Third Generation ML Realization
 Resilient distributed data sets (RDDs)
 Read-only collection of objects partitioned across a cluster
 Can be rebuilt if partition is lost.
 Operations on RDDs
 Transformations – map, flatMap, reduceByKey, sort, join, partitionBy
 Actions – Foreach, reduce, collect, count, lookup
 Programmer can build RDDs from
1. a file in HDFS
2. Parallelizing Scala collection - divide into slices.
3. Transform existing RDD - Specify operations such as Map, Filter
4. Change persistence of RDD Cache or a save action – saves to HDFS.
 Shared variables
 Broadcast variables, accumulators
[MZ10] Matei Zaharia, Mosharaf Chowdhury, Michael J. Franklin, Scott Shenker, and Ion Stoica. 2010. Spark:
cluster computing with working sets. In Proceedings of the 2nd USENIX conference on Hot topics in cloud
computing (HotCloud'10). USENIX Association, Berkeley, CA, USA, 10-10

12. 12
Data Flow in Spark and Hadoop

13. Logistic Regression: Spark VS Hadoop
13http://spark-project.org

14. Spark Use Cases
14
Ooyala
Uses Cassandra
for video data
personalization.
Pre-compute
aggregates VS
on-the-fly queries.
Moved to Spark
for ML and
computing views.
Moved to Shark for
on-the-fly queries –
C* OLAP aggregate
queries on
Cassandra 130 secs,
60 ms in Spark
Conviva
Uses Hive for
repeatedly running
ad-hoc queries on
video data.
Optimized ad-hoc
queries using Spark
RDDs – found Spark
is 30 times faster
than Hive
ML for connection
analysis and video
streaming
optimization.
Quantifind
Movie , video game
companies can
predict success of
new releases
Moved from Hadoop
to Spark and able to
run ML in
seconds, instead of
hours.

15. Instance of Architecture for Internet Traffic
Analysis Use Case

16. K-means Clustering Algorithm:
Mahout VS ML Over Storm
16

17. GraphLab: Ideal Engine for Processing Natural Graphs [YL12]
 Goals – targeted at machine learning.
 Model graph dependencies, be asynchronous, iterative, dynamic.
 Data associated with edges (weights, for instance) and vertices (user profile
data, current interests etc.).
 Update functions – lives on each vertex
 Transforms data in scope of vertex.
 Can choose to trigger neighbours (for example only if Rank changes
drastically)
 Run asynchronously till convergence – no global barrier.
 Consistency is important in ML algorithms (some do not even converge
when there are inconsistent updates – collaborative filtering).
 GraphLab – provides varying level of consistency. Parallelism VS consistency.
 Implemented several algorithms, including ALS, K-means, SVM, Belief
propagation, matrix factorization, Gibbs sampling, SVD, CoEM etc.
 Co-EM (Expectation Maximization) algorithm 15x faster than Hadoop MR – on
distributed GraphLab, only 0.3% of Hadoop execution time.[YL12] Yucheng Low, Danny Bickson, Joseph Gonzalez, Carlos Guestrin, Aapo Kyrola, and Joseph M.
Hellerstein. 2012. Distributed GraphLab: a framework for machine learning and data mining in the
cloud. Proceedings of the VLDB Endowment 5, 8 (April 2012), 716-727.

18. GraphLab 2: PowerGraph – Modeling Natural Graphs [1]
 GraphLab could not scale to Altavista web graph 2002, 1.4B vertices, 6.7B
edges.
 Most graph parallel abstractions assume small neighbourhoods – low degree
vertices
 But natural graphs (LinkedIn, Facebook, Twitter) – power law graphs.
 Hard to partition power law graphs, high degree vertices limit parallelism.
 GraphLab provides new way of partitioning power law graphs
 Edges are tied to machines, vertices (esp. high degree ones) span machines
 Execution split into 3 phases:
 Gather, apply and scatter.
 Triangle counting on Twitter graph
 Hadoop MR took 423 minutes on 1536 machines
 GraphLab 2 took 1.5 minutes on 1024 cores (64 machines)
[1] Joseph E. Gonzalez, Yucheng Low, Haijie Gu, Danny Bickson, and Carlos Guestrin (2012). "PowerGraph:
Distributed Graph-Parallel Computation on Natural Graphs." Proceedings of the 10th USENIX Symposium
on Operating Systems Design and Implementation (OSDI '12).

19. Thank You!
• Mail
vijay.sa@impetus.co.in
• LinkedIn
http://in.linkedin.com/in/vijaysrinivasagneeswaran
• Blogs
blogs.impetus.com
• Twitter
@a_vijaysrinivas.