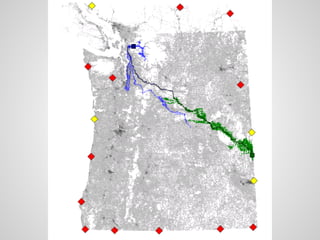
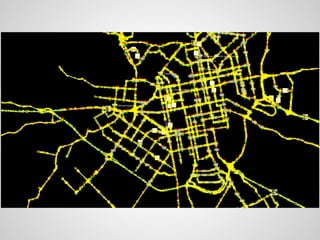
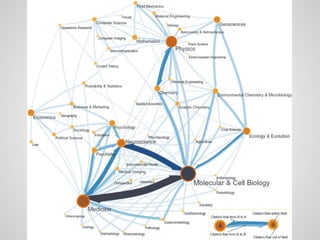
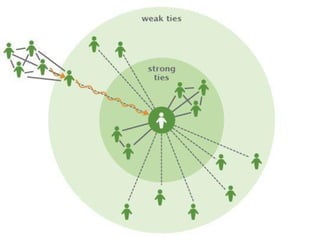
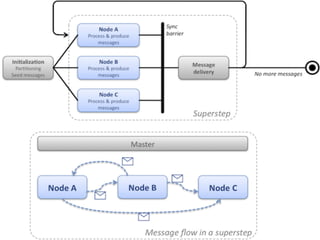
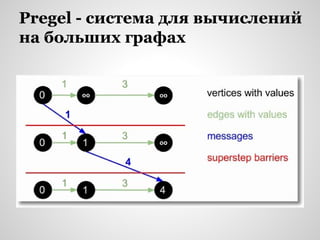
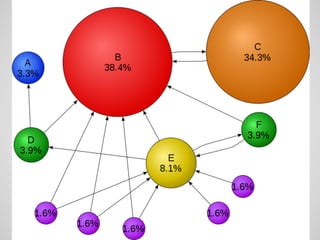
Доклад обсуждает использование алгоритмов и структур данных для обработки больших графов, охватывая теорию графов и практические применения в различных областях, таких как социология и транспортные сети. Основное внимание уделяется поиску кратчайших путей, включая оптимизации и алгоритмы, такие как A* и Dijkstra, а также вопросам хранения данных и устойчивости к ошибкам. Также акцентируется внимание на современных системах вычислений, таких как Pregel и Giraph, для работы с большими графами.

1. Докладчик: Алексей Зиновьев
Big Data algorithms and data structures
for large-scale graphs

2. О себе
● аспирант ОмГУ, математик
● занимаюсь теорией графов,
прогнозированием пробок, исследованием
транспортных систем
● большой фанат различных Maps API

3. BigData & Graph Theory

4. Откуда BigData есть быти?
BigData прошлого:
● Астрономический
вычисления
● Данные
многолетних
наблюдений за
погодой
● Данные торговых
операций
● Морские маршруты

5. А теперь
● Web-граф (модель Интернета)
● Граф почтовых сообщений
● Социологические исследования
● Дорожные графы
● Транзакции на PayPal
● Граф друзей на Facebook
● Анализ текстов, публикаций

8. Чемпионы-тяжеловесы
Граф Число
вершин
Число
ребер
Объем
данных
на диске
Прирост в
день
Web-граф 1 трлн 8 трлн 100 PB 300 TB
Facebook
(граф
друзей)
1 млрд 140 млрд 1 PB 15 TB
Дорожный
граф
Европы
18 млн 42 млн 20 GB 50 MB
Дорожный
графЕкб
120 000 260 000 400 MB 100 KB

9. ● найти ближайшую точку к данной на большом
множестве точек;
● расcтояние может быть любым, в том числе быть
длиной кратчайшего маршрута на графе.
Основные приложения
● сервисы рекомендаций, генетические исследования;
● распознавание образов;
● классификация текстов;
● рекомендательные и экспертные системы;
● динамическое размещение рекламы в Интернете.
Nearest Neighbor Search (NNS)

11. Эксперимент Милграма
● Hyper ANF - новый алгоритм, основанный на счетчиках
HyperLogLog и вычислении функции соседства
● HyperLogLog - статистический счетчик (6% отклонение,
5 - 7 bits)
● Диаметр Facebook - 10 hours, 1TB RAM
Facebook 4.74 712 M 69 G
Twitter 3.67 ---- 5G follows
MSN Messenger (1
month)
6.6 180 M 1.3 G arcs

12. ● поиск кратчайшего расстояния между двумя точками
● кластеризация и поиск компонент
● поиск min/max остовного дерева
● задача коммивояжера
● потоковые задачи
● построение моделей динамических графов,
развивающихся схоже с некоторыми реальными
совокупностями объектов (человечество; все научные
статьи; преступления; почтовая переписка)
Основные задачи на графах

15. Node Centrality Problem
Зачем искать множество центральных точек?
● влияние таких точек больше остальных
● удаление важных вершин снижает надежность
системы
Основные приложения
● астрофизика
● биоинформатика
● социальные связи
● дорожные сети
● изучение топологии интернета и выявление спама
● системы рекомендаций

16. Вопросы хранения больших
графов

17. ● матрица смежности
● матрица инцидентности
● список смежных вершин
● список ребер
● различные виды деревьев
● в виде стеков
и многие другие...
Все эти представления различаются по потребляемой
памяти и временной сложности выполнения
стандартных операций над графом.
Традиционные и не очень
структуры данных

18. ● граф в RAM, данные на диске в свободном формате
● граф в RAM, данные в неграфовой СУБД
● граф в RAM, данные в графовой СУБД
● граф не загружается целиком в RAM, обработка идет
частями, данные на диске в произвольном формате
● неграфовое представление в RAM, данные на диске в
файле или в СУБД любого типа
Для некоторых агрегационных вычислений граф не
требуется представлять в памяти в виде графа и
определять корректные операции
Способы работы с графом

19. ● Оптимальна для
сильносвязных сущностей
● Вершины, ребра, атрибуты
● Индексы на значения
атрибутов
● ACID
● REST API + Cypher
● Множество плагинов, включая
2d индекс
Neo4j: преимущества

21. ● Нет полноценного
горизонтального
масштабирования
● Плохо приспособлен для
размещения на нескольких
машинах
● Лимиты и платность
● Много маркетинга и
неоправданного использования
Neo4j: недостатки

22. Системы для вычисления на
больших графах

23. Решение некоторых графовых задач при помощи
MapReduce возможно, но не является оптимальным
● сложность сведения графовой задачи к модели key-
value
● большинство графовых алгоритмов построено на
итерационной обработке, что в M/R требует multiple
chained jobs, что влечет полное сохранение и загрузку
состояния графа (эта операция будет доминировать
по времени)
Think like a vertex…
Ограничения парадигмы
MapReduce

25. Определим две базовых операции
● Fusion - собираем информацию от соседей
● Diffusion - распостраняем информацию от вершины
соседям
Храним состояние графа в памяти в течение всей
обработки, сохраняя только конечное состояние и
некоторые промежуточные точки прогресса.
Теперь вместо определения mapper и reducer,
достаточно определить Vertex, который имеет значение
и список ребер, а также способен посылать сообщения
на каждой итерации.
Bulk Synchronous Parallel

27. Pregel - система для вычислений
на больших графах
В основе Pregel лежит вершинный подход, а сама
система основана на модели Bulk Synchronous Parallel
Программы обработки графов в Pregel представлены в
виде последовательностей итераций, которые
называются супершагами.
При выполнении супершага для каждой вершины
графа запускается определенная пользователем
функция, и все функции выполняются параллельно.

28. Pregel - система для вычислений
на больших графах

29. Pregel - система для вычислений
на больших графах
Вершины обмениваются сообщениями, а также могут
изменять свое состояние и состояние смежных ребер,
согласно полученной информации.
Если вершина не получила сообщений, то она
становится неактивной. Если все вершины не активны,
то работа алгоритма останавливается.
Pregel обеспечивает масштабируемость, устойчива к
ошибкам и позволяет применять произвольные
алгоритмы.

30. С++ API

32. Giraph - открытая система для
вычислений на больших графах
В основе Giraph лежат статьи Google о построении
собственной системы Pregel.
В свое время использовался в Facebook для анализа
социального графа.
В данный момент в Giraph добавлено несколько фич,
которых нет в Pregel: master computation, sharded
aggregators, edge-oriented input, out-of-core computation

33. Giraph - открытая система для
вычислений на больших графах
В данный момент доступна версия 1.0
В основе лежит модель Master/Workers, где
● Master - распределяет куски данных между Workers
и синхронизирует супершаги
● Worker - загружает свой кусок графа и выполняет
все вычисления, рассылает сообщения
Нет точки отказа, т.к. при падении текущего Master, на
его место заступает другой. При падении Worker
вычисления начинаются с последней checkpoint с
меньшим количеством workers. Очередь из
“заместителей” Master хранится в ZooKeeper

34. Альтернативная история

35. Дорожные графы

36. Не всякий граф - дорожный...
Назовем граф дорожным, если он может быть описан
как граф с положительными весами, приписанными к
ребрам.
Также часть ребер в таком графе может быть более
важной, чем остальная (магистральные шоссе,
выделенные линии связи). Это свойство может
использоваться в различных алгоритмах на
“дорожных” графах, чтобы вычислять кратчайшие
расстояния быстрее, чем на обычных графах.

37. Кратчайшее расстояние на
графе Европы
Поиск кратчайшего расстояния на графе - одна из
важнейших задач оптимизации, причем классические
подходы в данной области не оправдывают себя на
больших графах.

40. A* - эвристический
алгоритм
Каким образом можно улучшить алгоритм Дейкстры и
не просматривать целиком весь граф в процессе
построения кратчайшего маршрута?
Алгоритм поиска по первому наилучшему совпадению
(best first) на графе, который находит маршрут с
наименьшей стоимостью между двумя вершинами
Порядок обхода вершин определяется эвристической
функцией «расстояние + стоимость» (обычно
обозначаемой как f(v)= g(v) + h(v))

42. Двунаправленный поиск
Алгоритм состоит:
● прямого поиска, аналогичного одиночному поиску;
● обратного поиска;
● операции определения принадлежности листа
другому дереву поиска.
Соединив пути получаем искомый путь. Если два
поиска осуществляются параллельно — это ещё больше
экономит время на получение искомого пути по
сравнению с однонаправленным поиском.

44. Требования к системе обработки
● Необходимо быстро (10 мс) находить кратчайшее
расстояние между двумя точками
● Линейность алгоритмов
● Этап предварительной обработки (препроцессинг)
● Не хранить все расстояния между вершинами (O(n^2)
по памяти)
● Ответ может быть точным с определенной
вероятностью
● Учет геоспецифики графа
● Использование сжатия и перекодировки для хранения
на диске

45. Двухфазовые алгоритмы
Все подобные алгоритмы работают в два этапа. Первый этап
включает в себя предварительную обработку графа без
использования информации о том, между какими
вершинами надо найти кратчайшее расстояние. Результаты
обработки сохраняются в базу данных.
Второй этап - выполнение запроса к базе данных. В момент
выполнения запроса известны узлы, между которыми
необходимо найти кратчайшее расстояние.
Основное предположение состоит в том, что дорожная сеть
слабо изменяется со временем и фазу обработки не нужно
выполнять слишком часто.

46. Алгоритмы для вычисления
кратчайшего расстояния
ALT: [Goldberg & Harrelson 05], [Delling & Wagner 07]
RE: [Gutman 05], [Goldberg et al. 07]
HH: [Sanders & Schultes 06]
CH: [Geisberger et al. 08]
TN: [Geisberger et al. 08]
HL: [Abraham et al. 11]
Dijkstra ALT RE HH CH TN HL
2 008 300 24 656 2444 462.0 94.0 1.8 0.3

47. A* with landmarks (ALT)
● Выбираем подмножество вершин (случайно, например)
● Вычисляем расстояния между ними
● Вычисление нижних границ (функции h(v)) для A*
расстояний между ними происходит за O(1)
Поиск может быть направлен с двух сторон.
Низкий уровень сканирования: для того чтобы найти путь
из 1000 вершин в графе с 3 млн, было просканировано
всего 10 тысяч вершин.

49. Reach (RE)
Формализуем интуицию автомобилиста:
● он не ищет объезд вдалеке
● он стремится попасть поскорее но основную скоростную
магистраль
● он стремится гнать по основной магистрали, не
обращая внимание на дороги меньшего класса
важности, двигаясь по направлению к цели

51. Contraction hierarchies (CH)
Это техника для поиска кратчайших путей в созданном на
предварительной стадии особом “контрактном” графе.
Дуга может быть пропущена, если есть альтернативные
пути.
Большую роль играет класс и важность дороги.
Для поиска в новом графе используется двунаправленный
алгоритм Дейкстры.

52. Transit nodes (TN)
Граф разбивается на подграфы так, что для каждого
подграфа, есть небольшой набор узлов R, таких, что все
кратчайшие пути между вершинами* из региона проходят
через узел из R.
Фаза препроцессинга:
● найти R для каждого региона
● найти для каждой вершины его transit node из R
● вычислить все пары кратчайших путей между
транзитными узлами из R
* больше определенной величины d

54. Затруднительные ситуации

55. Оптимизационные задачи на
больших графах
Однако, при решении оптимизационных задач на графах,
изменяющих структуру самого графа, фаза
препроцессинга длиною в несколько часов становится
бессмысленной.
Пример задачи: есть 1 млрд рублей на развитие
дорожной сети. Каким образом можно инвестировать его,
чтобы уменьшить среднее время, затрачиваемое на
ежедневные межрайонные корреспонденции граждан?
Еще пример: дорожная сеть подверглась воздействию
стихии, ожидается еще один удар. Где проложить новые
дороги, чтобы система была максимально устойчивой?

61. I/O Efficient Algorithms and Data
Structures
● Традиционный подход состоит в случайном чтении из
RAM
● Однако, стоит помнить, что уровней памяти много
● Чем дальше от CPU, тем больше и медленнее
● Данные перемещаются между уровнями большими
блоками
● Часто OS берет на себя предсказание и подгрузку
● Диск в 10^6 медленнее RAM
● Разбиение на небольшие блоки и выполнение
операций внутри каждого блока с объединением
результата уменьшает число I/O операций

62. Graphs and Memory Errors
Что может привести к ошибкам?
● космическое излучение
● битый кусок винчестера
● ошибка при передаче данных из RAM в кэш
Чем чревато?
● классические алгоритмы (слияние списков, например)
не готовы к ошибкам
● выходом из строя критического оборудования
● редкость ошибок - миф (эксперимент Google)
Разработка алгоритмов, устойчивых к ошибкам, ведется
уже 50 лет!

63. Итоги
● Для анализа большого графа
достаточно небольшого
вычислительного кластера
● Структуры данных и способ
хранения очень сильно зависят
от задачи и выбранного
алгоритма
● Невозможна хаотичная работа
с большими данными без
соответствующего
математического аппарата и
программного обеспечения