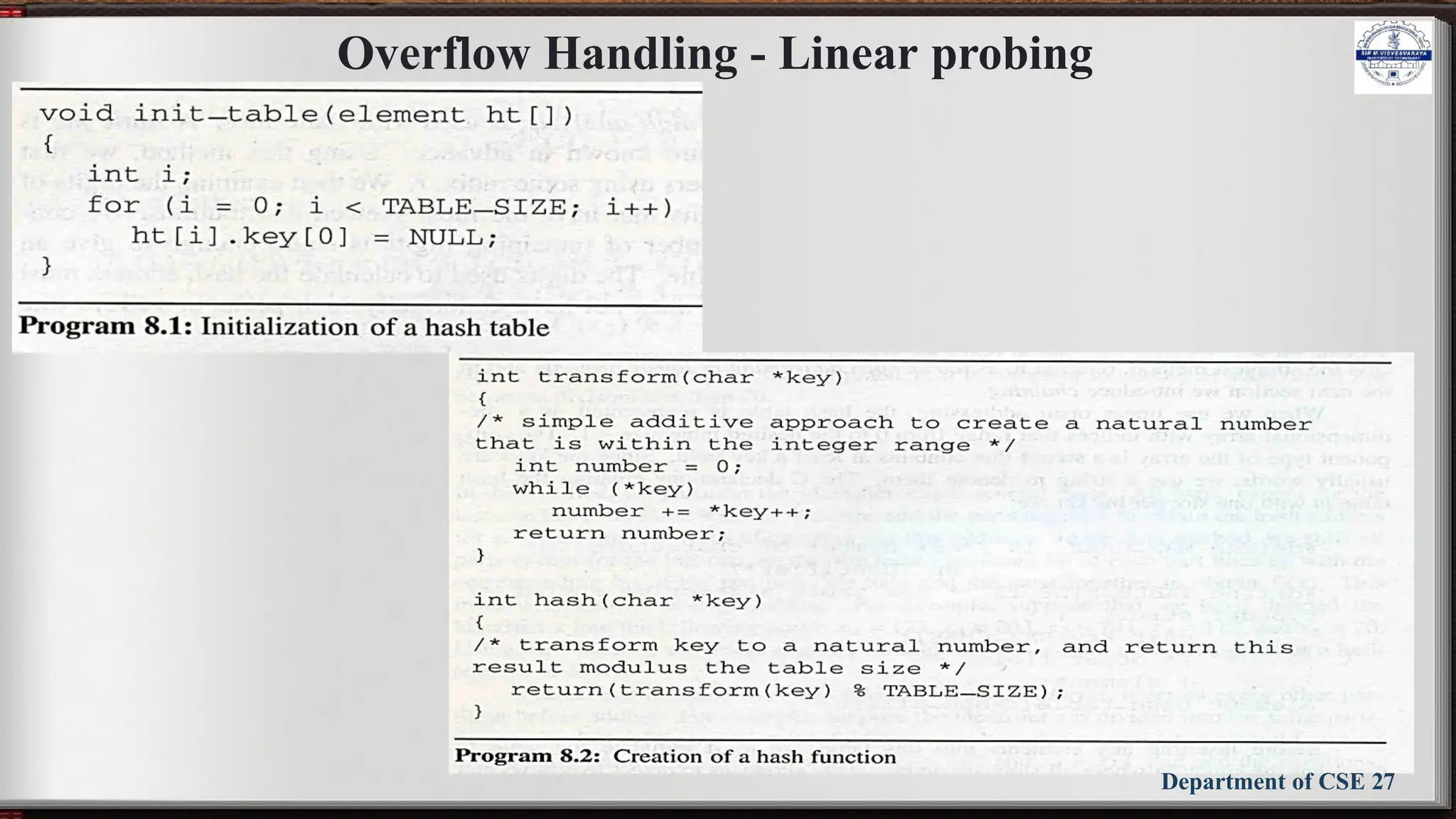
The document outlines the syllabus for the Data Structures and Applications course (BCS304) at Sir M Visvesvaraya Institute of Technology, detailing five modules covering topics such as arrays, linked lists, trees, graphs, and hashing techniques. It includes objectives, outcomes, and references for textbooks and resources relevant to data structure concepts. The course aims to equip students with understanding and practical skills in representing and applying various data structures to solve real-world problems.

























![Overflow Handling - Linear probing
Department of CSE 26
Linear open addressing (Linear probing)
• Compute f(x) for identifier x
• Examine the buckets:
ht[(f(x)+j)%TABLE_SIZE], 0 ≤ j ≤ TABLE_SIZE
• The bucket contains x.
• The bucket contains the empty string (insert to it)
• The bucket contains a nonempty string other than x
(examine the next bucket) (circular rotation)
• Return to the home bucket ht[f(x)],
if the table is full we report an error condition and
exit](https://image.slidesharecdn.com/bcs304module5slides-241029150507-b6e5bfba/75/BCS304-Module-5-slides-DSA-notes-3rd-sem-26-2048.jpg)