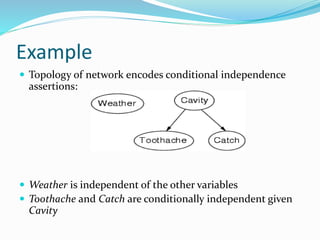
This document discusses Bayesian networks, which use a directed acyclic graph structure to represent conditional independence relationships between variables and compactly specify joint probability distributions. An example Bayesian network is given showing how the topology encodes that weather is independent of other variables and that toothache and catching a cold are conditionally independent given having a cavity. Reasons for using and learning Bayesian networks are explained, including that they provide an intuitive way to incorporate causal knowledge and allow for efficient inference queries.

1. Bayesian probabilistic interference
Prof. Neeraj Bhargava
Kapil Chauhan
Department of Computer Science
School of Engineering & Systems Sciences
MDS University, Ajmer

2. Outline
 What is a Bayesian network?
 Why Bayesian networks are useful?
 Why learn a Bayesian network?
 Semanitcs
 What is probabilities
 Types of probabilities
 More probabilities

3. What is a Bayesian network?
 A simple, graphical notation for conditional independence
assertions and hence for compact specification of full joint
distributions
 Syntax:
 a set of nodes, one per variable

 a directed, acyclic graph (link ≈ "directly influences")
 a conditional distribution for each node given its parents:
P (Xi | Parents (Xi))
 In the simplest case, conditional distribution represented
as a conditional probability table (CPT) giving the
distribution over Xi for each combination of parent values

4. Example
 Topology of network encodes conditional independence
assertions:
 Weather is independent of the other variables
 Toothache and Catch are conditionally independent given
Cavity

5. Why is a Bayesian network?
 Expressive language
 Finite mixture models, Factor analysis, Kalman filter,…
 Intuitive language
 Can utilize causal knowledge in constructing models
 Domain experts comfortable building a network
 General purpose “inference” algorithms
 P(Bad Battery | Has Gas, Won’t Start)
 Exact: Modular specification leads to large computational
efficiencies
 Approximate: “Loopy” belief propagation
Gas
Start
Battery

6. Why Learning?
data-based
-Answer Wizard, Office 95, 97, & 2000
-Troubleshooters, Windows 98 & 2000
-Causal discovery
-Data visualization
-Concise model of data
-Prediction
knowledge-based
(expert systems)

7. Semantics
The full joint distribution is defined as the product of the local
conditional distributions:
P (X1, … ,Xn) = πi = 1 P (Xi | Parents(Xi))
e.g., P(j  m  a  b  e)
= P (j | a) P (m | a) P (a | b, e) P (b) P (e)
n

8. Constructing Bayesian networks
 1. Choose an ordering of variables X1, … ,Xn
 2. For i = 1 to n
 add Xi to the network
 select parents from X1, … ,Xi-1 such that
P (Xi | Parents(Xi)) = P (Xi | X1, ... Xi-1)
This choice of parents guarantees:
P (X1, … ,Xn) = πi =1 P (Xi | X1, … , Xi-1)
(chain rule)
= πi =1P (Xi | Parents(Xi))
(by construction)
n
n

9. Assignment
 Explain Bayesian probabilistic interference with
example.