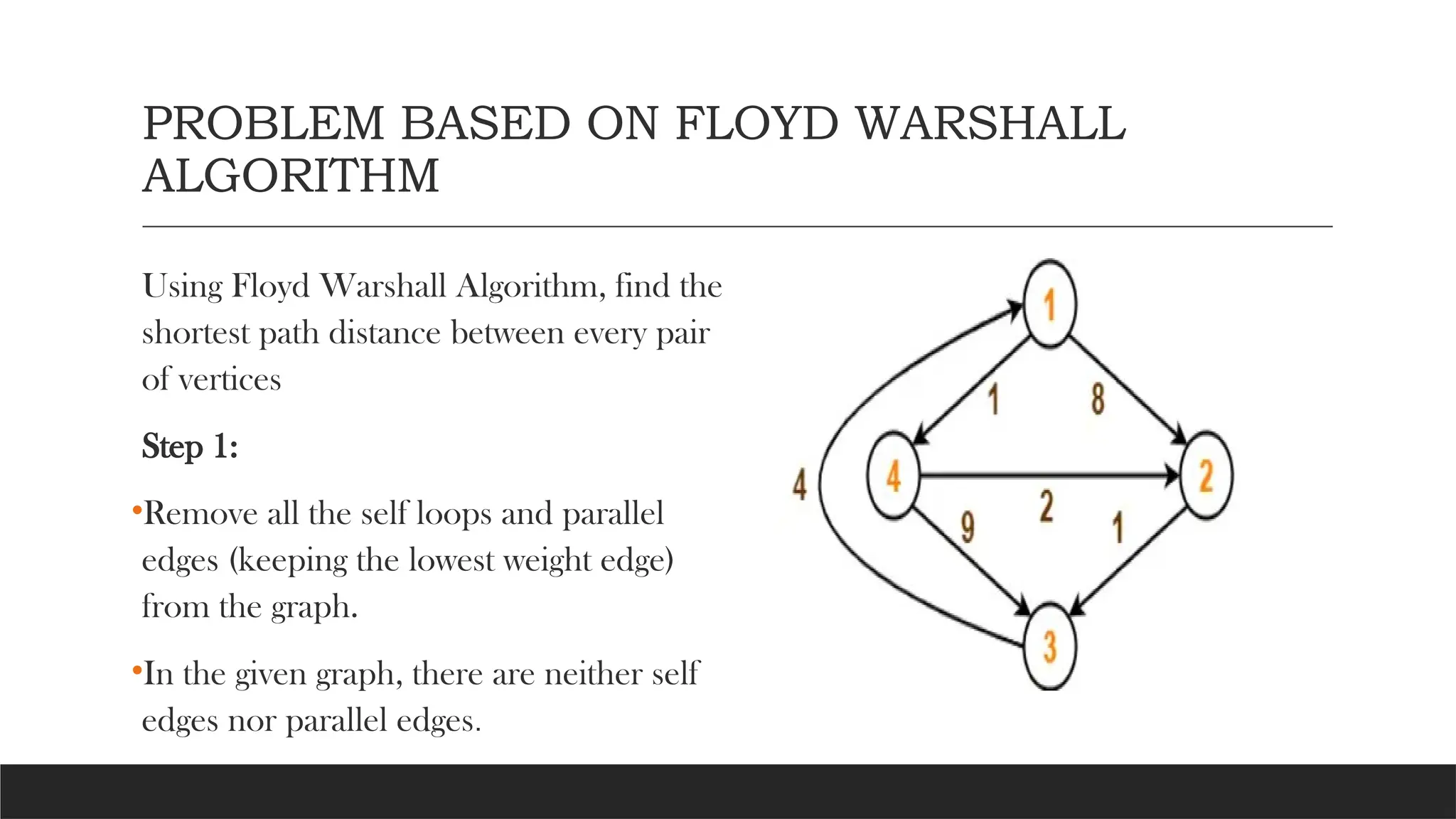
Floyd's algorithm is a dynamic programming-based method for finding the shortest paths between all pairs of vertices in a graph, with a time complexity of O(n^3). It is particularly useful for dense graphs and offers advantages like handling negative edge weights and providing transitive closures. The algorithm has applications in computer network routing, transportation logistics, and road network analysis.

1. Floyd
Algorithm
TEAM MEMBERS:
ABISHAKE S
ADARSH M S
AMIRDHESH S
ARANGANATHAN K

2. Introduction
Floyd's Algorithm is a graph pathfinding
algorithm that finds the shortest path
between all pairs of vertices in a graph. It
is based on dynamic programming and is
highly efficient. This presentation will
explain the algorithm and how it can be
used to optimize pathfinding

3. Graph Representation
Before we dive into Floyd's Algorithm, it is important
to understand how graphs are represented. A graph
is a collection of vertices and edges that connect
them. There are two types of graphs: directed and
undirected. In a directed graph, the edges have a
direction, while in an undirected graph, they do not.

4. Dynamic Programming
Floyd's Algorithm uses dynamic programming to
find the shortest path between all pairs of vertices
in a graph. Dynamic programming is a technique
where a problem is solved by breaking it down into
smaller subproblems and solving each
subproblem only once. This greatly reduces the
number of computations required.

5. Floyd Warshall Algorithm:

6. Time complexity
•Floyd Warshall Algorithm consists of three loops over
all the nodes.
•The inner most loop consists of only constant
complexity operations.
•Hence, the asymptotic complexity of Floyd Warshall
algorithm is O(n3
).
•Here, n is the number of nodes in the given graph.

7. When Floyd Warshall Algorithm Is Used?
•Floyd Warshall Algorithm is best suited for dense
graphs.
•This is because its complexity depends only on the
number of vertices in the given graph.
•For sparse graphs, Johnson’s Algorithm is more
suitable.

8. PROBLEM BASED ON FLOYD WARSHALL
ALGORITHM
Using Floyd Warshall Algorithm, find the
shortest path distance between every pair
of vertices
Step 1:
•Remove all the self loops and parallel
edges (keeping the lowest weight edge)
from the graph.
•In the given graph, there are neither self
edges nor parallel edges.

9. Step 2:
•Write the initial distance matrix.
•It represents the distance between
every pair of vertices in the form of
given weights.
•For diagonal elements (representing
self-loops), distance value = 0.
•For vertices having a direct edge
between them, distance value = weight
of that edge.
•For vertices having no direct edge
between them, distance value = .
∞

10. Step 3
The last matrix D4 represents the shortest path distance between every pair of vertices.

11. Advantage:
Floyd's Algorithm has several advantages over other pathfinding
algorithms:
It can handle negative edge weights, unlike Dijkstra's
Algorithm.
It is highly efficient, with a time complexity of O(n^3).
It can be used to find the transitive closure of a graph, which
is useful in many applications.

12. Application
1. Routing in computer networks: The Floyd algorithm can be used to calculate the shortest paths
between all routers in a network. This information is crucial for efficient packet routing and
minimizing network congestion.
2. Transportation and logistics: The algorithm can be used to determine the most efficient routes
for goods or vehicles in a transportation network. It helps in optimizing delivery schedules,
reducing fuel consumption, and minimizing travel time.
3. Transportation and logistics: The algorithm can be used to determine the most efficient routes
for goods or vehicles in a transportation network. It helps in optimizing delivery schedules,
reducing fuel consumption, and minimizing travel time.
4. Road network analysis: Governments and transportation authorities can use the Floyd algorithm
to analyze road networks and determine the shortest paths between different locations. This
information is valuable for urban planning, traffic management, and emergency response systems.

13. Conclusion
Floyd's Algorithm is a powerful tool for optimizing
graph pathfinding. Its use of dynamic programming
and ability to handle negative edge weights make it
a valuable addition to any developer's toolkit. By
understanding the algorithm and its advantages, we
can build more efficient and effective applications.