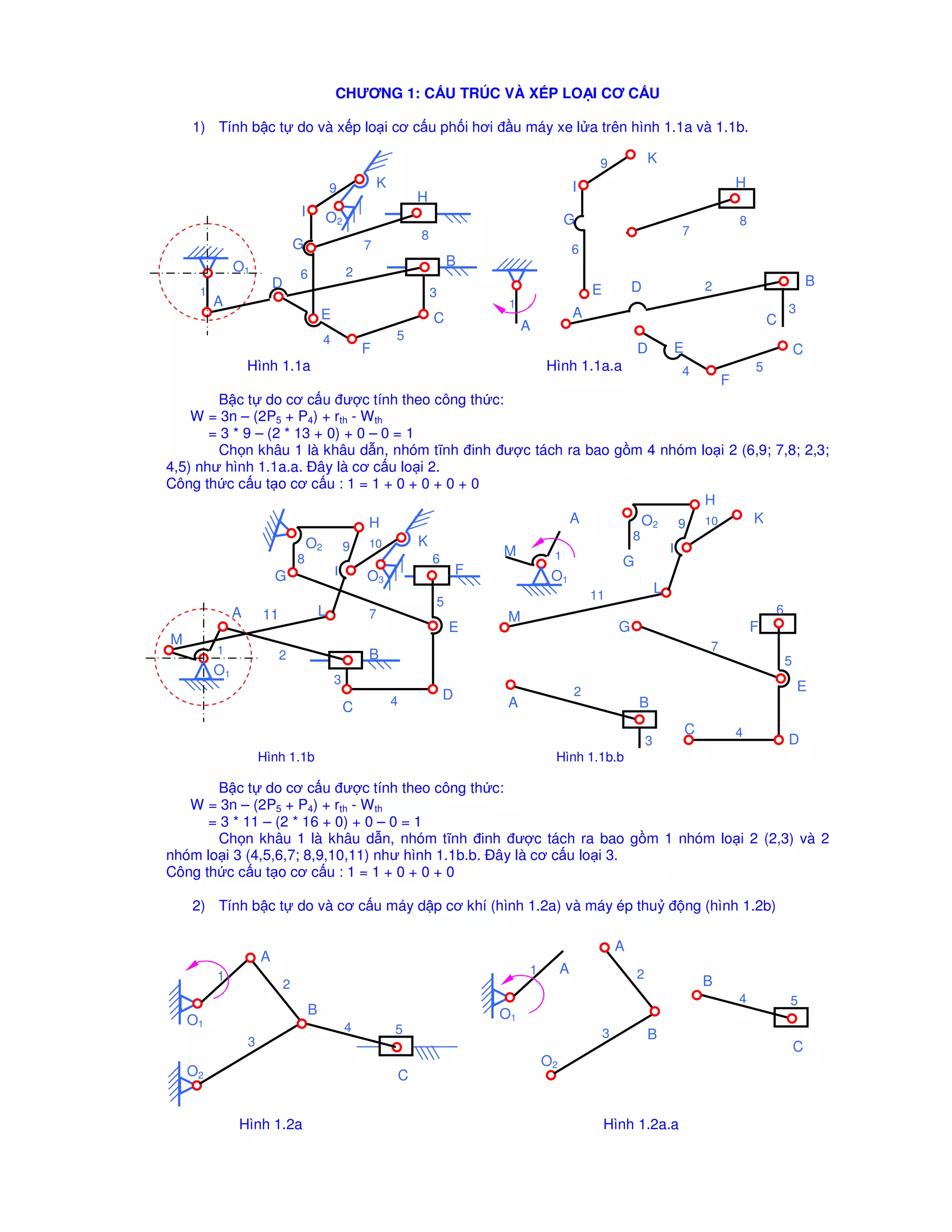
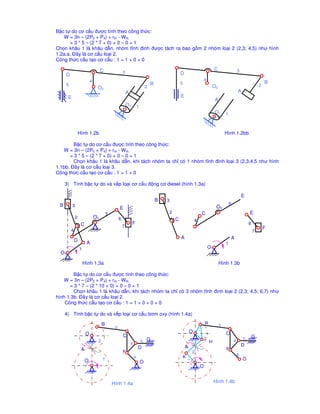
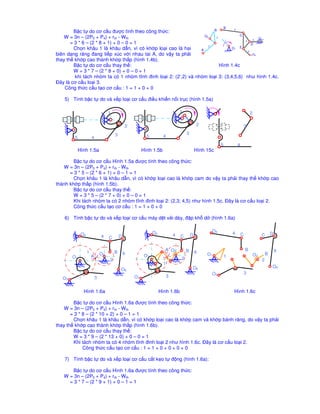
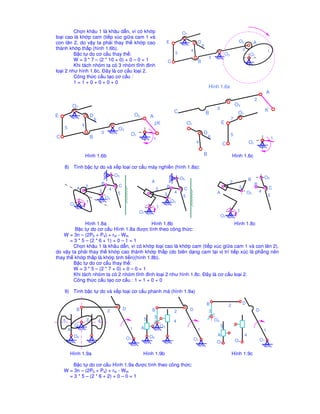
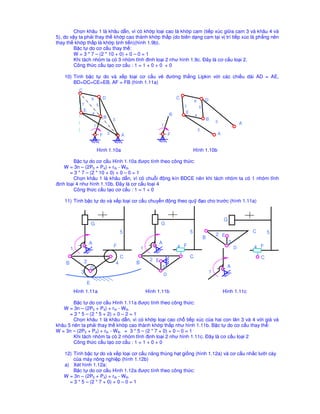
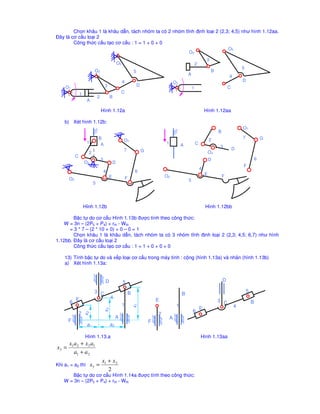
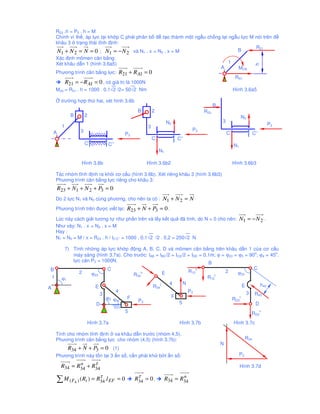
Tài liệu trình bày các phương pháp tính toán bậc tự do và cấu trúc của các hệ thống cơ khí khác nhau, sử dụng các công thức toán học cụ thể. Mỗi phần đều nêu rõ cách xác định bậc tự do cho từng loại cấu trúc, đồng thời minh họa bằng hình ảnh và công thức tính. Nhấn mạnh việc hình thành nhóm tĩnh và việc thay thế các khâu cao thành khâu thấp để tối ưu hóa cấu trúc.

1. CHƯƠNG 1: C U TRÚC VÀ X P LO I CƠ C U
1) Tính b c t do và x p lo i cơ c u ph i hơi ñ u máy xe l a trên hình 1.1a và 1.1b.
9 K
9 K I H
H
I O2 G 8
8 7
G 7 6
O1 B
6 2
D D 2 B
1 3 E
A 1 3
E C A C
A
4 5
F D E C
Hình 1.1a Hình 1.1a.a 4 5
F
B c t do cơ c u ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 9 – (2 * 13 + 0) + 0 – 0 = 1
Ch n khâu 1 là khâu d n, nhóm tĩnh ñinh ñư c tách ra bao g m 4 nhóm lo i 2 (6,9; 7,8; 2,3;
4,5) như hình 1.1a.a. ðây là cơ c u lo i 2.
Công th c c u t o cơ c u : 1 = 1 + 0 + 0 + 0 + 0
H
H A O2 9 10 K
K 8
O2 9 10 I
8 6
M 1
G
G I O3 F O1
11
L
5
A 11 L 7 6
M
E G F
M 7
1 2 B 5
O1
3
2 E
4 D
C A B
C 4
3 D
Hình 1.1b Hình 1.1b.b
B c t do cơ c u ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 11 – (2 * 16 + 0) + 0 – 0 = 1
Ch n khâu 1 là khâu d n, nhóm tĩnh ñinh ñư c tách ra bao g m 1 nhóm lo i 2 (2,3) và 2
nhóm lo i 3 (4,5,6,7; 8,9,10,11) như hình 1.1b.b. ðây là cơ c u lo i 3.
Công th c c u t o cơ c u : 1 = 1 + 0 + 0 + 0
2) Tính b c t do và cơ c u máy d p cơ khí (hình 1.2a) và máy ép thu ñ ng (hình 1.2b)
A
A
1 1 A 2
2 B
4 5
B O1
O1 4 5 3 B
3 C
O2
O2 C
Hình 1.2a Hình 1.2a.a

2. B c t do cơ c u ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 7 + 0) + 0 – 0 = 1
Ch n khâu 1 là khâu d n, nhóm tĩnh ñinh ñư c tách ra bao g m 2 nhóm lo i 2 (2,3; 4,5) như hình
1.2a.a. ðây là cơ c u lo i 2.
Công th c c u t o cơ c u : 1 = 1 + 0 + 0
C C 3
3 D
D
4 4
5 B 5 B
2 O2 2
O2
A A
E E
A
O1 1
O1 1
Hình 1.2b Hình 1.2bb
B c t do cơ c u ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 7 + 0) + 0 – 0 = 1
Ch n khâu 1 là khâu d n, khi tách nhóm ta ch có 1 nhóm tĩnh ñinh lo i 3 (2,3,4,5 như hình
1.1bb. ðây là cơ c u lo i 3.
Công th c c u t o cơ c u : 1 = 1 + 0
3) Tính b c t do và x p lo i cơ c u ñ ng cơ diesel (hình 1.3a)
E
B 3
B 3 5
E O3
5 2 C E
2 O3 6 C 4
C F 6
7 F
4 7
A A
D A 1
1 O1
O1
Hình 1.3a Hình 1.3b
B c t do cơ c u ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 7 – (2 * 10 + 0) + 0 – 0 = 1
Ch n khâu 1 là khâu d n, khi tách nhóm ta ch có 3 nhóm tĩnh ñinh lo i 2 (2,3; 4,5; 6,7) như
hình 1.3b. ðây là cơ c u lo i 2.
Công th c c u t o cơ c u : 1 = 1 + 0 + 0 + 0
4) Tính b c t do và x p lo i cơ c u bơm oxy (hình 1.4a)
B B 3
3
O O C
C G
G 2 5
2 5 H 4
4 D
D A E
A
E 2’
K 6
1 6 O
O O 1
O
Hình 1.4a Hình 1.4b

3. 3
B
B
B c t do cơ c u ñư c tính theo công th c:
O2 C
W = 3n – (2P5 + P4) + rth - Wth 2 G
1 4 5
= 3 * 6 – (2 * 8 + 1) + 0 – 0 = 1 D
2’
Ch n khâu 1 là khâu d n, vì có kh p lo i cao là hai O1 E
A 6
biên d ng răng ñang ti p xúc v i nhau tai A, do v y ta ph i O6
thay th kh p cao thành kh p th p (hình 1.4b).
B c t do cơ c u thay th : Hình 1.4c
W = 3 * 7 – (2 * 8 + 0) + 0 – 0 = 1
khi tách nhóm ta có 1 nhóm tĩnh ñinh lo i 2: (2’,2) và nhóm lo i 3: (3,4,5,6) như hình 1.4c.
ðây là cơ c u lo i 3.
Công th c c u t o cơ c u : 1 = 1 + 0 + 0
5) Tính b c t do và x p lo i cơ c u ñi u khi n n i tr c (hình 1.5a)
1 1 2
2 2 3
3 3
5 4 5 4
5 4
Hình 1.5a Hình 1.5b Hình 15c
B c t do cơ c u Hình 1.5a ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 6 + 1) + 0 – 1 = 1
Ch n khâu 1 là khâu d n, vì có kh p lo i cao là kh p cam do v y ta ph i thay th kh p cao
thành kh p th p (hình 1.5b).
B c t do cơ c u thay th :
W = 3 * 5 – (2 * 7 + 0) + 0 – 0 = 1
Khi tách nhóm ta có 2 nhóm tĩnh ñinh lo i 2: (2,3; 4,5) như hình 1.5c. ðây là cơ c u lo i 2.
Công th c c u t o cơ c u : 1 = 1 + 0 + 0
6) Tính b c t do và x p lo i cơ c u máy d t v i dày, ñ p kh d (hình 1.6a)
O4 O4 4
O4 4 D C C D
4 C D C
A O2 B B 6
1 O2 B 6 6 O1 B
O1 A O1 1 O2
2 2 2
1
O6 O6
O6
O3 3
O3 3 O3 3
Hình 1.6a Hình 1.6b Hình 1.6c
B c t do cơ c u Hình 1.6a ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 8 – (2 * 10 + 2) + 0 – 1 = 1
Ch n khâu 1 là khâu d n, vì có kh p lo i cao là kh p cam và kh p bánh răng, do v y ta ph i
thay th kh p cao thành kh p th p (hình 1.6b).
B c t do cơ c u thay th :
W = 3 * 9 – (2 * 13 + 0) + 0 – 0 = 1
Khi tách nhóm ta có 4 nhóm tĩnh ñinh lo i 2 như hình 1.6c. ðây là cơ c u lo i 2.
Công th c c u t o cơ c u : 1 = 1 + 0 + 0 + 0 + 0
7) Tính b c t do và x p lo i cơ c u c t k o t ñ ng (hình 1.6a):
B c t do cơ c u Hình 1.6a ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 7 – (2 * 9 + 1) + 0 – 1 = 1

4. Ch n khâu 1 là khâu d n, vì có kh p O7
lo i cao là kh p cam (ti p xúc gi a cam 1 và
con lăn 2, do v y ta ph i thay th kh p cao E D O2 A
6
thành kh p th p (hình 1.6b). 4 2
5 1
B c t do cơ c u thay th : O3 O1
3
W = 3 * 7 – (2 * 10 + 0) + 0 – 0 = 1 C B
Khi tách nhóm ta có 3 nhóm tĩnh ñinh
lo i 2 như hình 1.6c. ðây là cơ c u lo i 2.
Công th c c u t o cơ c u :
1=1+0+0+0+0
Hình 1.6a
A
2
O7 O3
3 K
C B O7
E D O2 A
6 7
4 2K O7 E
5 O3
3 O1 D 5
C B 1 6 1
4 C O1
Hình 1.6b B Hình 1.6c
8) Tính b c t do và x p lo i cơ c u máy nghi n (hình 1.8a):
O5 O5
O5 B
B A 2
2 C B
A B C 3 C
3 4 2 4
5 3 4 A O3
5 5
O3
1 O3
O1
1
O1 1
O1
Hình 1.8a Hình 1.8b Hình 1.8c
B c t do cơ c u Hình 1.8a ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 6 + 1) + 0 – 1 = 1
Ch n khâu 1 là khâu d n, vì có kh p lo i cao là kh p cam (ti p xúc gi a cam 1 và con lăn 2),
do v y ta ph i thay th kh p cao thành kh p th p (do biên d ng cam t i v trí ti p xúc là ph ng nên
thay th kh p th p là kh p t nh ti n)(hình 1.8b).
B c t do cơ c u thay th :
W = 3 * 5 – (2 * 7 + 0) + 0 – 0 = 1
Khi tách nhóm ta có 2 nhóm tĩnh ñinh lo i 2 như hình 1.8c. ðây là cơ c u lo i 2.
Công th c c u t o cơ c u : 1 = 1 + 0 + 0
9) Tính b c t do và x p lo i cơ c u phanh má (hình 1.9a)
B 2 D
B 2 D B D 3 D
2
5 3
5 3 4 4 O3
O3 O3 5
A 1 A 1 1
O5 O5 A 4
O1 O1 O4 O1
O5
Hình 1.9a Hình 1.9b Hình 1.9c
B c t do cơ c u Hình 1.9a ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 6 + 2) + 0 – 0 = 1

5. Ch n khâu 1 là khâu d n, vì có kh p lo i cao là kh p cam (ti p xúc gi a cam 3 và khâu 4 và
5), do v y ta ph i thay th kh p cao thành kh p th p (do biên d ng cam t i v trí ti p xúc là ph ng nên
thay th kh p th p là kh p t nh ti n)(hình 1.9b).
B c t do cơ c u thay th :
W = 3 * 7 – (2 * 10 + 0) + 0 – 0 = 1
Khi tách nhóm ta có 3 nhóm tĩnh ñinh lo i 2 như hình 1.9c. ðây là cơ c u lo i 2.
Công th c c u t o cơ c u : 1 = 1 + 0 + 0 + 0
10) Tính b c t do và x p lo i cơ c u v ñư ng th ng Lipkin v i các chi u dài AD = AE,
BD=DC=CE=EB, AF = FB (hình 1.11a)
C
6 D C D
6
7 5 7 5
E E
4 B
B 4
3 B
3 A
1 1
2
F 2 A F A
Hình 1.10a Hình 1.10b
B c t do cơ c u Hình 1.10a ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 7 – (2 * 10 + 0) + 0 – 0 = 1
Ch n khâu 1 là khâu d n, vì có chu i ñ ng kín BDCE nên khi tách nhóm ta có 1 nhóm tĩnh
ñ nh lo i 4 như hình 1.10b. ðây là cơ c u lo i 4
Công th c c u t o cơ c u : 1 = 1 + 0
11) Tính b c t do và x p lo i cơ c u chuy n ñ ng theo qu ñ o cho trư c (hình 1.11a)
G
G G
5 5 C 5
2 E
B
A A 3
1
F 1 4 F D 4 F
C C C
2 2 E
B 4 B
D 3 A
3 1
D
E
Hình 1.11a Hình 1.11b Hình 1.11c
B c t do cơ c u Hình 1.11a ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 5 + 2) + 0 – 2 = 1
Ch n khâu 1 là khâu d n, vì có kh p lo i cao ch ti p xúc c a hai con lăn 3 và 4 v i giá và
khâu 5 nên ta ph i thay th kh p cao thành kh p th p như hình 1.11b. B c t do cơ c u thay th :
W = 3n – (2P5 + P4) + rth - Wth = 3 * 5 – (2 * 7 + 0) + 0 – 0 = 1
Khi tách nhóm ta có 2 nhóm tĩnh ñ nh lo i 2 như hình 1.11c. ðây là cơ c u lo i 2
Công th c c u t o cơ c u : 1 = 1 + 0 + 0
12) Tính b c t do và x p lo i cơ c u nâng thùng h t gi ng (hình 1.12a) và cơ c u nh c lư i cày
c a máy nông nghi p (hình 1.12b)
a) Xét hình 1.12a:
B c t do cơ c u Hình 1.12a ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 5 – (2 * 7 + 0) + 0 – 0 = 1

6. Ch n khâu 1 là khâu d n, tách nhóm ta có 2 nhóm tĩnh ñ nh lo i 2 (2,3; 4,5) như hình 1.12aa.
ðây là cơ c u lo i 2
Công th c c u t o cơ c u : 1 = 1 + 0 + 0
O5
O3
3
O5 2
5
O3 5 B
A 4
4 O1 D
O1 3 D C
1
1 C
2 B
A
Hình 1.12a Hình 1.12aa
b) Xét hình 1.12b:
O7
B
B 7 G
O7 2
1 A 1 C
A 3
7 G D
2 O3
C
3 D 6
O3 D
F
4
4 6
O5 E F
O5 E F 5
5
H nh 1.12b Hình 1.12bb
B c t do cơ c u Hình 1.13b ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 7 – (2 * 10 + 0) + 0 – 0 = 1
Ch n khâu 1 là khâu d n, tách nhóm ta có 3 nhóm tĩnh ñ nh lo i 2 (2,3; 4,5; 6,7) như hình
1.12bb. ðây là cơ c u lo i 2
Công th c c u t o cơ c u : 1 = 1 + 0 + 0 + 0
13) Tính b c t do và x p lo i cơ c u trong máy tính : c ng (hình 1.13a) và nhân (hình 1.13b)
a) Xét hình 1.13a:
D 5 D
3 C B 5
B
E 4
6 E 3 C B
1 1
x1
E 4
x3
2 6
x2
2
A A
F F
a1 a2
Hình 1.13.a Hình 1.13aa
x1 a 2 + x 2 a1
x3 =
a1 + a 2
x1 + x 2
Khi a1 = a2 thì x3 =
2
B c t do cơ c u Hình 1.14a ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth

7. = 3 * 6 – (2 * 8 + 0) + 0 – 0 = 2
Ch ng t cơ c u co 2 khâu d n, Ch n khâu 1 và 2 là khâu d n, tách nhóm ta có 1 nhóm tĩnh
ñ nh lo i 3 (3, 4, 5, 6) như hình 1.13aa. ðây là cơ c u lo i 3
Công th c c u t o cơ c u : 2 = 2 + 0
b) Xét hình 1.14b:
5
5
z
x
3 4
3 4
6 y
x
2 6
2
1
h 1
Hình 1.13b Hình 1.13bb
xy
z=
h− y
y
hi khâu 2 c ñ nh: = const = t , do v y z = tx
h− y
B c t do cơ c u Hình 1.13b ñư c tính theo công th c:
W = 3n – (2P5 + P4) + rth - Wth
= 3 * 6 – (2 * 8 + 0) + 0 – 0 = 2
Ch ng t cơ c u co 2 khâu d n, Ch n khâu 1 và 6 là khâu d n, tách nhóm ta có 1 nhóm tĩnh
ñ nh lo i 3 (2, 3, 4, 5) như hình 1.13bb. ðây là cơ c u lo i 3
Công th c c u t o cơ c u : 2 = 2 + 0

8. CHƯƠNG 2: PHÂN TÍCH ð NG H C CƠ C U PH NG LO I 2
1) Xác ñ nh v n t c và gia t c c a dao bào E trong cơ c u máy bào x c (hình 2.1a) khi tay quay
1 quay ñ u v i v n t c góc ω1 = 10s −1 t i v trí ϕ1 = 45 o . Cho bi t kích thư c các khâu c a
cơ c u: l AB = l ED = 0,2m ; l AC = lCD = 0,3m ; a = 0,35m.
a e5≡e4
ak B d3≡d4
2
ω3 1
E C ϕ1 p
3
4
5 A ω1
D
b1≡b2
b3
Hình 2.1a Hình 2.1b
B1 ≡ B2 ≡ B3, khâu 1 n i v i khâu 2 b ng kh p
quay, khâu 2 n i v i khâu 3 b ng kh p trư t b3
V B1 = V B2 ≠ VB3 π
k d3 ≡d4
Giá tr : V B = V B = ω1.l AB = 10.0,2 = 2m / s , có n
1 2 b3 n
phương vuông góc v i khâu AB, chi u theo chi u v n t c e4
góc khâu 1. e4 ≡ e5
V B3 = VB 2 + VB3 B2 (1) b1≡b2
Hình 2.1c
Trong phương trình (1), V B3 vuông góc v i BC,
V B3 B 2 có phương song song v i BC.
VB2
Ch n t l xích ñ v : µV = (m / s / mm) . Ho ñ v n t c ñư c v như hình 2.1b.
pb2
ðo giá tr véc tơ ( pb3 ) bi u di n v n t c ñi m B3 và nhân v i t l xích ta thu ñư c giá tr th c v n
t c ñi m B3.
V B3 pb3
ω3 = = µV .
l BC l BC
V B3 l
Vì = BC , t ñó suy ra v n t c c a ñi m D
V D3 lCD
E4 ≡ E5 và khâu 4 n i v i khâu 5 b ng kh p quay:
V E5 = VE 4 = VD 4 + VE 4 D4 (2)
Trong phương trình này: V E 4 có phương th ng ñ ng. V E 4 D4 có phương vuông góc v i
DE. Ho ñ ñư c v như hình 2.1b.
Ta ño ño n pe5 và nhân v i t l xích ñã ch n s có giá tr v n t c khâu 5, chi u ñi lên.
Tương t ta cũng xác ñ nh ñư c gia t c:
a B1 = a B2 = ω1 l AB = 100.0,2 = 20m / s 2 có chi u hư ng t B ñi vào A
2
a B3 = a B2 + a B3 B2 + a k
M t khác a B3 = a B C + aτ C , do v y
n
B3
3
a B3 = a B C + aτ C = a B 2 + a B3 B 2 + a k
n
B3
(3)
3

9. Trong phương trình (3) :
n 2
a B C = ω3 .l AB ; ñã xác ñ nh v giá tr có phương chi u hư ng t B ñi vào C.
3
aτ C = ε 3 .l AB = ? ; phương vuông góc v i BC.
B3
a k = 2ω 2 .V B3 B2 = 2ω3 .µV b2 b3 ; Phương chi u l y theo chi u V B3 B 2 quay ñi m t góc 900 theo
chi u ω3 .
a B3 B 2 = ? , phương song song v i BC.
a B2
Phương trình (3) ch t n t i 2 n s , ch n t l xích ho ñ gia t c: µa = (m / s 2 / mm) .
πb2
Cách gi i ñư c trình bày trên hình 2.1c
Các giá tr ñư c ño tr c ti p trên các véc tơ bi u di n tương ng sau ñó nhân v i t l xích ñã ch n.
Xác ñ nh gia t c góc khâu 3:
b n b3
ε 3 = µa 3
l BC
Xác ñ nh gia t c ñi m D3 cũng b ng phương pháp ñ ng d ng
a E 4 = a D 4 + a E D + aτ D
n
E4 4
(4)
4 4
Cách lý lu n cũng tương tư. Cách gi i trình bày trên hình 2.1c
0
2) Tính v n t c và gia t c ñi m D2 (∠ DBC = 120 ) trên con trư t 2 c a cơ c u cu lít t i v trí
ϕ1=900. Tay quay AB quay ñ u v i v n t c góc ω1 = 20s-1. Cho bi t kích thư c các khâu c a
cơ c u: lAB = lBD = 0,5lBC = 0,2m.
ϕ1 p
d2
1 2 b3 b3
A B D
ω1 ε3 d2n π
3 ak b1 ≡ b2 n
b3
ω3 b1 ≡ b2 k
C
d2
Hình 2.2a Hình 2.2b Hình 2.2c
S tương quan kích thư c ñã cho ta th y r ng tam giác ABC là n a tam giác ñ u,
(∠ABC=600) BD thu c khâu 2. ð xác ñ nh v n t c ñi m D, trư c tiên ta ph i bi t v n t c ñi m B2 và
v n t c góc khâu 2, sau áp d ng ñ nh lý h p v n t c s thu ñư c v n t c ñi m D. Khâu 2 trư t trong
khâu 3 và quay theo khâu 3 cho nên t c ñ góc khâu 2 cũng chính là t c ñ góc khâu 3.
B1 ≡ B2 ≡ B3, khâu 1 n i v i khâu 2 b ng kh p quay, khâu 2 n i v i khâu 3 b ng kh p trư t
V B1 = V B2 ≠ VB3
Giá tr : V B1 = V B 2 = ω1.l AB = 20.0,2 = 4m / s , có phương vuông góc v i khâu AB, chi u theo
chi u v n t c góc khâu 1.
V B3 = V B 2 + V B3 B 2 (1)
Trong phương trình (1), V B3 vuông góc v i BC, V B3 B2 có phương song song v i BC
Trong trư ng h p ñ c bi t này ta không c n ch n t l xích. Ho ñ v n t c ñư c v như hình 2.2b.
Tam giác pb2b3 ñ ng d ng v i tam giác BCA, ta tính ñư c v n t c ñi m b3: V B = V B / 2 = 2m / s .
3 2

10. V B3 2
T c ñ góc khâu 3 và khâu 2: ω 2 = ω3 = = = 5rad / s . Chi u ñư c xác ñ nh như hình v
l BC 0,4
V D2 = V B 2 + VD2 B2 (2)
Trong phương trình (2) ta ñã bi t v n t c ñi m B2 , VD2 B2 = ω 2 .l BD = 5.0,2 = 1m / s .
Chi u hư ng t trên xu ng theo chi u ω2 và vuông góc v i BD. Ho ñ ñư c v ti p như hình 2.2b.
Giá tr v n t c ñi m D ñư c tính:
VD 2 = V B 2 + V D2 B2 = 4 + 1 = 5m / s
Tương t ta cũng tính ñư c gia t c ñi m D2:
a B1 = a B 2 ≠ a B3
a B1 = a B2 = ω1 .l AB = 400.0,2 = 80m / s 2
2
a B3 = a B 2 + a B3 B 2 + a k
a B3 = a B C + aτ C
n
B3
3
a B2 + a B3 B2 + a k = a B C + aτ C
n
B3
(2)
3
Trong phương trình trên (2) Ta có ñư c:
a B 2 : ðã xác ñ nh; a B3 B 2 : Giá tr chưa bi t, phương song song v i BC.
a k = 2ω3 .V B3 B 2 = 2.5.2 3 = 20 3m / s 2
a B C = ω3 .l BC = 25.0,4 = 10m / s 2
n 2
3
aτ C = ε 3 .l BC = ? , có phương vuông góc v i BC.
B3
Phương trình (2) t n t i 2 n s , Ho ñ gia t c ñư c v như hình 2.1c
Gia t c góc khâu 2 và khâu 3 ñư c tính như sau:
aτ C
B
ε 2 = ε3 = 3
l BC
 n
aB 
τ  ak 
a B C =  a B2 − ( 3
+ ) sin 60 o + a B tg 60 o
n
o o 
3
 cos 60 sin 60  3
 
3
= (80 − 5 − 40) + 10 3 = 47,63m / s 2
2
aτ C 47,63
B
ε 2 = ε3 = 3 = = 119,075rad / s 2
l BC 0,4
a D 2 = a B 2 + a D B + aτ B
n
D2 2
(3)
2 2
Trong phương trình (3) Ta ñã bi t:
a D B = ω 2 .l BD = 25.0,2 = 5m / s 2
n 2
2 2
aτ B = ε 2 .l BD = 119,075.0,2 = 28,815m / s 2
D2
Ho ñ gia t c ñư c v trên hình 2,2c

11. Giá tr gia t c ñi m D ñư c tính: a D2 = (80 + 5)2 + 28,815 2 = 88,27 m / s 2
3) Tính v n t c và gia t c khâu 3 c a cơ c u tính tang m t góc, n u tay quay AB quay ñ u v i
-1 o
v n t c góc ω= 10s , t i v trí ϕ1 = 60 . Cho trư c h = 0,05m (hình 2.3a).
B
ak b3, b2
2 p
ϕ1
3 1
k
C A π
h b1
b2, b3
b1
Hình 2.3a Hình 2.3b Hình 2.3c
Vì khâu 3 chuy n ñ ng t nh ti n, cho nên m i ñi m trên khâu 3 ñ u có v n t c và gia t c như
nhau. Chúng ta ñi xác ñ nh v n t c và gia t c ñi m B3 .
B1 ≡ B2 ≡ B3 . Khâu 1 n i v i khâu2 b ng kh p t nh ti n, khâu 2 n i v i khâu 3 b ng kh p quay:
V B1 ≠ VB 2 = V B3
3 3
V B1 = ω1.l AB = 2 .0,05.10 = = 0,577 m / s
3 3
V B 2 = V B1 + V B 2 B1 (1)
//BC //AB
Phương trình ch t n t i hai n s là giá tr v n t c ñi m B2 và v n t c tương ñ i gi a 2 ñi m B1 và
B2. Ho ñ véc tơ v n t c ñư c v như hình 2.3b.
3
V n t c ñi m B2 ñư c tính như sau: V B 2 = 2VB 2 = 0,67 m / s. chi u ñư c xác ñ nh như trên
3
ho ñ v n t c (hình 2.3b).
Tương t gia t c ta cũng có: a B1 ≠ a B 2 = a B3
2 3 3
a B1 = ω1 .l AB = 100.2 .0,05 = 10 m / s2
3 3
a B 2 = a B1 + a B 2 B1 + a k
//BC // AB
3 3
a k : có giá tr là 2.ω1.VB 2 B1 = 2.10. = 10 m / s2 .
6 3
o
Phương chi u theo chi u c a V B B quay ñi m t góc 90 theo chi u ω1 . Ho ñ gia t c
2 1
ñư c v như hình 2.3c. Giá tr gia t c khâu 3 ñư c tính:
3 3 3
a B 2 = a B3 = 2 a k = 2.10. . = 6,7 m / s 2
3 3 3
4) Tính v n t c và gia t c ñi m C (hình 2.4a), v n t c góc và gia t c góc c a các khâu 2 và 3
trong cơ c u 4 khâu b n l t i v trí ∠ABC = ∠BCD = 90o , n u tay quay AB quay ñ u v i v n
t c góc ω1= 20s-1. Cho trư c kích thư c c a các khâu 4lAB = lBC = lCD = 0,4m.
π
B ω2
C c2,c3
1 2
b1, b2, c2,c3
A ω1 3
ω3 p
D b1, b2
Hình 2.4a Hình 2.4b Hình 2.4c

12. B1 ≡ B2. Khâu 1 n i v i khâu 2 b ng kh p quay:
V B1 = VB 2
V B1 = ω1.l AB = 20.0,1 = 2m / s
Tương t : C2 ≡ C3 và VC 2 = VC 3
VC 2 = V B2 + VC 2 B 2 (1)
⊥CD ⊥BC
Phương trình ch t n t i hai n s là giá tr v n t c ñi m C2 và v n t c tương ñ i gi a 2 ñi m C2
và B2. Ho ñ véc tơ v n t c ñư c v như hình 2.3b.
T ho ñ ta th y răng v n t c ñi m C và v n t c ñi m B thu c khâu 2 là b ng nhau, do v y khâu 2
chuy n ñ ng t nh ti n t c th i: ω2 = 0.
V n t c góc khâu 3:
VC 3 2
ω3 = = = 5rad / s
lCD 0,4
Chi u ñư c xác ñ nh theo chi u VC3 như hình v .
Xác ñ nh gia t c:
a B1 = a B2
a B1 = ω1 .l AB = 400.0,1 = 40m / s 2
2
aC 2 = aC 3 = aC D + aτ D = a B 2 + aC B + aτ B
n
C3
n
C2 2
(2)
3 2 2
Trên phương trình 2:
n
aC D : Có giá tr b ng: ω23 . lCD = 25 . 0,4 = 10m/s2
3
aτ D : Giá tr chưa bi t, có phương vuông góc v i CD
C3
n
aC B : có giá tr b ng 0 vì ω2 = 0.
2 2
aτ B : Giá tr chưa bi t, có phương vuông góc v i BC.
C2 2
Phương trình ch còn t n t i 2 n s là giá tr c a 2 gia t c ti p. Cách gi i ñư c trình bày trên
hình 2.4c.
Gia t c ði m C bây gi ch t n t i gia t c pháp có chi u hư ng t C ñi vào D và có giá tr là
10m/s2. Gia t c ti p b ng 0.
Gia t c ti p trong chuy n ñ ng tương ñ i gi a ñi m C2 ñ i v i ñi m B2 là aτ B ñư c bi u
C2 2
di n b i véc tơ b2 c 2 có giá tr là : 40 – 10 = 30m/s2.
2
Gia t c góc khâu2 ñư c xác ñ nh: ε2 = 30 / 0,4 = 75rad/s . chi u xác ñ nh như trên hình v .
5) Tính v n t c và gia t c ñi m C và v n t c góc và gia t c góc c a thanh truy n 2 trong cơ c u
tay quay con trư t (hình 1.5a) khi tay quay và thanh truy n th ng hàng. Bi t tay quay AB
quay ñ u v i v n toccs góc ω1 = 20s-1 và kích thư c các khâu : 2lAB = lBC = 0,2m.
p c2, c3
B ω2 C
A 3
1 2 c2n, c2, c3
ω1 π
b1, b2
b1, b2
Hình 2.5a Hình 2.5b Hình 2.5c

13. B1 ≡ B2 . Khâu 1 n i v i khâu 2 b ng kh p quay:
V B1 = VB 2
V B1 = ω1.l AB = 20.0,1 = 2m / s
Tương t : C2 ≡ C3 và VC 2 = VC 3
VC 2 = V B2 + VC 2 B 2 (1)
//AC ⊥BC
Phương trình ch t n t i hai n s là giá tr v n t c ñi m C2 và v n t c tương ñ i gi a 2 ñi m C2
và B2. Ho ñ véc tơ v n t c ñư c v như hình 2.5b.
T ho ñ ta th y răng v n t c ñi m C b ng 0, v n t c ñi m B và v n t c tương ñ i gi a ñi m C ñ i v i
ñi m B là b ng nhau v giá tr và ngư c chi u nhau. V n t c góc khâu 2 ñư c tính:
VC2 B2 2
ω2 = = = 10rad / s
lBC 0,2
Chi u xác ñ nh như hình v (hình 2.5a)
Xác ñ nh gia t c:
a B1 = a B2
a B1 = ω1 .l AB = 400.0,1 = 40m / s 2
2
aC2 = aC3 = aB2 + aC B + aτ B
n
C2 2
(2)
2 2
Trên phương trình 2:
n
aC B : có giá tr b ng: ω2 .lBC = 100.0,2 = 20m / s 2
2
2 2
aτ B : Giá tr chưa bi t, có phương vuông góc v i BC.
C2 2
a : có phương song song v i AC, giá tr chưa bi t.
C2
Phương trình ch còn t n t i 2 n s là giá tr c a gia t c ti p tương ñ i và gia t c tuy t ñ i
ñi m C . Cách gi i ñư c trình bày trên hình 2.5c.
2
Gia t c ði m C có chi u như hình v và có giá tr b ng 40 + 20 = 60m/s .
Gia t c ti p trong chuy n ñ ng tương ñ i gi a ñi m C2 ñ i v i ñi m B2 là aτ B ñư c bi u
C2 2
n
di n b i véc tơ c2 c2 có giá tr là 0, do v y gia t c góc khâu 2 b ng 0
6) Tính v n t c và gia t c ñi m D trên khâu 2 c a cơ c u tay quay con trư t (hình 2.6a) t i v trí
o -1
các góc ∠CAB = ∠CDB = 90 . Bi t tay quay AB quay ñ u v i v n t c góc ω1 = 20s và kích
thư c các khâu lAB =lCD = 0,5lBC = 0,1m.
B D π,d2 c2,c3
2
1 p b1,b2,c2,c3
C
A
ω1 3 b1,b2
Hình 2.6a Hình 2.6b Hình 2.6c
B1 ≡ B2 . Khâu 1 n i v i khâu 2 b ng kh p quay:
V B1 = VB 2 và V B1 = ω1.l AB = 20.0,1 = 2m / s
Tương t : C2 ≡ C3 và VC 2 = VC3
VC 2 = V B2 + VC 2 B 2 (1)
//AC ⊥BC

14. Phương trình ch t n t i hai n s là giá tr v n t c ñi m C2 và v n t c tương ñ i gi a 2 ñi m C2
và B2. Ho ñ véc tơ v n t c ñư c v như hình 2.6b.
T ho ñ ta nh n th y r ng v n t c t i ñi m B và ñi m C thu c khâu 2 ñ u b ng nhau, khâu 2 chuy n
ñ ng t nh ti n t c th i, m i ñi m trên khâu 2 ñ u có v n t c như nhau v i giá tr b ng 2m/s, ω2 = 0.
VB1 = VB2 = VC2 = VC3 = VD2
Xác ñ nh gia t c:
a B1 = a B2
a B1 = ω1 .l AB = 400.0,1 = 40m / s 2
2
Chi u hư ng t B ñi vào A
aC2 = aC3 = aB2 + aC B + aτ B
n
C2 2
(2)
2 2
Trên phương trình 2:
n 2
aC B : có giá tr b ng: ω2 .l BC = 0
2 2
aτ B : Giá tr chưa bi t, có phương vuông góc v i BC.
C2 2
a : có phương song song v i AC, giá tr chưa bi t.
C2
Phương trình ch còn t n t i 2 n s là giá tr c a gia t c ti p tương ñ i và gia t c tuy t ñ i
ñi m C. Cách gi i ñư c trình bày trên hình 2.6c.
Áp d ng ñ nh lý ñ ng d ng thu n: Hình n i các mút véc tơ bi u di n gia t c tuy t ñ i thì ñ ng
d ng thu n v i hình n i các ñi m tương ng trên cùng m t khâu. Ta tìm ñư c ñi m d2 tương ng v i
ñi m D2 trên khâu 2, ñó chính là c c ho ñ gia t c. Gia t c ñi m D b ng 0.
7) Tính v n t c góc và gia t c góc c a các khâu trong cơ c u culít (hình 2.7) v trí góc ∠BAC =
o
90 , n u tay quay AB quay ñ u v i v n t c góc ω1 = 10rad/s và kích thư c các khâu là
lAB=lAC=0,2m.
b1 π
A 1 B p
2
ω1 3 b3n
ak
ε3 b2,b3
ω3 b1 k b2,b3
C
Hình 2.7a Hình 2.7b Hình 2.7c
B1 ≡ B2 ≡ B3 . Khâu 1 n i v i khâu2 b ng kh p t nh ti n, khâu 2 n i v i khâu 3 b ng kh p quay:
V B1 ≠ VB 2 = V B3 và VB1 = ω1.l AB = 10.0,2 = 2m / s
V B 2 = V B1 + V B 2 B1 (1)
⊥BC //AB
Phương trình (2) t n t i 2 n s . Cách gi i ñư c trình bày trên ho ñ v n t c (hình 2.7b).
V n t c ñi m B2 và B3 ñư c xác ñ nh theo ho ñ :
VB2 = VB1 2 = 2 2m / s
VB3 2 2
ω3 = = = 10 s −1
l BC 0,2 2
Như v y: ω1 = ω2 = ω3 = 10rad/s, chi u xác ñ nh như hình v .
Tương t gia t c ta cũng có: a B1 ≠ a B 2 = a B3
a B1 = ω1 .l AB = 100.0,2 = 20m / s 2 có chi u hư ng t B ñi vào A.
2
aB2 = aB1 + a B2 B1 + ak = aB C + aτ C
n
B3
(2)
3

15. Trong phương trình trên (2) Ta có ñư c:
a B1 : ðã xác ñ nh; aB2 B1 : Giá tr chưa bi t, phương song song v i BC.
ak = 2ω1.VB2 B1 = 2.10.2 = 40m / s 2 , chi u l y theo chi u VB2B1 quay ñi m t góc 90o theo chi u
ω1 (hình 2.7a).
a B C = ω3 .l BC = 10.0,2 2 = 20 2m / s 2
n 2
3
aτ C = ε 3 .l BC = ? , có phương vuông góc v i BC.
B3
Phương trình ch còn t n t i 2 n s . Cách gi i ñư c trình bày trên hình 2.7c.
n
T hình v ta tính ñư c gia t c ti p c a ñi m B3 , bi u di n b i b3 b3 :
aτ C = 20 2m / s 2
B 3
20 2
Gia t c góc khâu 3: ε3 = = 100rad / s 2
0,2 2
Do khâu 1 quay ñ u và t c ñ góc khâu 2 luôn b ng khâu 3 cho nên: ε1 = ε2 = 0.
8) Tìm v n t c góc l n nh t c a culits 2 (hình 2.8a) qua v n t c góc ω1 c a tay quay 1 cho trư c
ng v i ba trư ng h p:
a) lAB = 0,075m; lAC = 0,3m
b) lAB = 0,075m; lAC = 0,225m
c) lAB = 0,075m; lAC = 0,150m
p
B c2
1 2 α
α C A
3 B C
A ω b ,b
1 1 2
Hình 2.8a Hình 2.8b Hình 2.8c
B1 ≡ B2 . Khâu 1 n i v i khâu 2 b ng kh p quay:
VB1 = VB2 và VB1 = ω1.l AB
Ch n B2 làm c c ta vi t ñư c phương trình véc tơ tính v n t c ñi m C2.
VC2 = VB2 + VC2 B2 (1)
//BC ⊥BC
Phương trình trên ch t n t i 2 n s giá tr . Ho ñ v n t c ñư c v như hình 2.8b.
G i α là góc h p b i phương v n t c ñi m B v i phương c a khâu BC. T c ñ góc c a khâu 2
ñư c tính :
VC2 B2 sin α
ω2 = = VB2 (2)
l BC lBC
Trong ñ ng th c (2), mu n v n t c góc khâu 2 ñ t c c ñ i thì sinα = 1 và lBC bé nh t.
Khi ñó α = 90o và A, B, C th ng hàng (hình 2.8c)
ω1.l AB 0,075 ω
a) ω2 max = = ω1 = 1
l AC − l AB 0,3 − 0,075 3
ω1.l AB 0,075 ω
b) ω2 max = = ω1 = 1
l AC − l AB 0,225 − 0,075 2
ω1.l AB 0,075
c) ω2 max = = ω1 = ω1
l AC − l AB 0,150 − 0,075

16. 9) Tính v n t c ñi m D trên khâu 3 c a cơ c u xy lanh quay (hình 2.9a và 2.9b) t i v trí các góc
∠BAC=∠BCD = 90o, n u tay quay AB quay ñ u v i v n t c góc ω1 = 20rad/s và kích thư c các
khâu là lAB = lCD = 0,1m, lAC = 0,173m.
a) Xét hình 2.9a:
b1,b2
B D p α
α 2 VD
1 c2
3
A ω1 C
Hình 2.9a
Ta th y r ng ñi m D thu c khâu 3, khâu 3 ñang quay quanh C. Khâu 3 quay theo khâu 2 do ñó
t c ñ góc khâu 2 và khâu 3 là như nhau. ð tính ñư c v n t c ñi m D chúng ta ch c n xác ñ nh
ñư c v n t c góc khâu 3 thì v n ñ coi như ñư c gi i quy t xong.
B1 ≡ B2 . Khâu 1 n i v i khâu 2 b ng kh p quay:
VB1 = VB2 và VB1 = ω1.l AB = 20.0,1 = 2m / s
Ch n B2 làm c c ta vi t ñư c phương trình véc tơ tính v n t c ñi m C2.
VC2 = VB2 + VC2 B2 (1)
//BC ⊥BC
Phương trình trên ch t n t i 2 n s giá tr . Ho ñ v n t c ñư c v như hình 2.a1.
G i α là góc h p b i phương AB v i phương c a khâu BC. T c ñ góc c a khâu 2 ñư c tính :
VC2 B2 cos α 0,1
ω2 = = VB2 =2 2 = 6,2rad / s
lBC lBC 0,1 + 0,1732
V n t c ñi m D ñư c tính như sau:
VD3 = ω3.lCD = 6,2.0,1 = 0,62m / s
Chi u ñư c xác ñ nh theo chi u ω3 như hình 2.9a.
b) Xét hình 2.9b:
2
D b3
B
α VD
1 α b1,b2
3
A ω1 C p
Hình 2.9b Hình 2.9b1
Tương t ta cũng tính ñư c v n t c góc khâu 3 thông qua phương trình véc tơ:
VB3 = VB2 + VB3 B2 (2)
⊥BC //BC
Ho ñ v n t c cũng gi ng như trư ng h p trên (hình 2.9b1)
Giá tr v n t c ñi m D và phương chi u cùng k t qu như trên.
10) Tính v n t c và gia t c c a ñi m F trên cơ c u sàng t i l c (hình 2.10a) n u tay quay AB
quay ñ u v i v n t c góc ω1 = 20rad/s t i v trí AB và CE th ng ñ ng. BC n m ngang. Cho
trư c kích thư c các khâu: lAB = lCE = lDE = lBC/3 = 0,5lDF = 0,1m.
π π f4,f5
B C ,
2 c2,c3
1 e3,e4
3 e4,f4,f5 b1,b2,c2,c3
A ω1
E p
4
F
b1, b2 c2,c3
D 5
Hình 2.10a Hình 2.10b Hình 2.10c1 Hình 2.10c2

17. ðây là m t t h p g m 2 cơ c u h p thành: Cơ câu 4 khâu b n l ABCD (tương t bài s 4) và
cơ c u tay quay con trư t DEF (tương t bài s 6)
B1 ≡ B2 . Khâu 1 n i v i khâu 2 b ng kh p quay:
VB1 = VB2 và VB1 = ω1.l AB = 20.0,1 = 2m / s
Tương tư như nh ng bài ñã gi i, v trí các khâu c a cơ c u v trí ñ c bi t.Khâu 2 chuy n ñ ng
t nh ti n t c th i:
ω2 = 0, V n t c ñi m B và C c a khâu 2 là b ng nhau
V B 2 = VC 2 = VC 3
Tương t trên khâu 4, v n t c ñi m E và ñi m F cũng băng nhau:
VC 3
V E 3 = VE 4 = VF4 = V F5 =
2
Khâu 4 t nh ti n th c th i ω4 = 0. VF = 1m/s
V n t c góc khâu 3:
VC 3 2
ω3 = = = 10rad / s
lCD 0,2
Xác ñ nh gia t c:
a B1 = a B2
a B1 = ω1 .l AB = 400.0,1 = 40m / s 2
2
aC 2 = aC 3 = aC D + aτ D = a B 2 + aC B + aτ B
n
C3
n
C2 2
(2)
3 2 2
Trên phương trình 2:
n
aC D : Có giá tr b ng: ω23 . lCD = 100 . 0,2 = 20m/s2
3
aτ D : Giá tr chưa bi t, có phương vuông góc v i CD
C3
n
aC B : có giá tr b ng 0 vì ω2 = 0.
2 2
τ
aC B : Giá tr chưa bi t, có phương vuông góc v i BC.
2 2
Phương trình ch còn t n t i 2 n s là giá tr c a 2 gia t c ti p. Cách gi i ñư c trình bày trên
hình 2.10c1.
Gia t c ði m C bây gi ch t n t i gia t c pháp có chi u hư ng t C ñi vào D và có giá tr là
20m/s2. Gia t c ti p b ng 0.
Gia t c ñi m E3 b ng n a gia t c ñi m C.
Xác ñ nh gia t c ñi m F
a F4 = a F5 = a E 4 + a F E + aτ E
n
F4 4
(2)
4 4
Trên phương trình 2:
n 2
a F E : có giá tr b ng: ω 4 .l EF = 0
4 4
aτ E : Giá tr chưa bi t, có phương vuông góc v i EF.
F4 4
a : có phương song song v i DF, giá tr chưa bi t.
F4
Phương trình ch còn t n t i 2 n s là giá tr c a gia t c ti p tương ñ i và gia t c tuy t ñ i
ñi m C. Cách gi i ñư c trình bày trên hình 2.10c2 ( K ti p c a hình 2.10c1)
Do s tương quan ñ ng d ng c i cơ c u ta có h th c:
aF 4 aE4 a E 4 .DE 10.0,1
= a F4 = = = 5m / s 2
DE DF DF 0,2

18. CHƯƠNG 3: PHÂN TÍCH L C H C TRÊN CƠ C U PH NG LO I 2
1) M t con trư t chuy n ñ ng nhanh d n v i gia t c a = 10m/s2. Không k t i ma sát trên m t
trư t, tính công su t ngo i l c P ñ y v t chuy n ñ ng khi v t có v n t c 5m/s. Bi t kh i lư ng
c a con trư t là m = 2 kg (hình 3.1).
Áp d ng nguyên lý D A lăm be, thu ñư c:
P
P + Pqt = 0 V a
Pqt = m.a = 2.10 = 20N.
P = 10N
Công su t ngo i l c P ñ y v t chuy n ñ ng v i v n t c 5m/s: Hình 3.1
P.V = P.V cos( P,V ) = 20.5 = 100W
2) Hãy tính mômen c a l c quán tính c a bánh ñà trong th i gian m máy: Bi t lúc b t ñ u m
máy v n t c góc b ng 0 và sau 3 giây v n t c tăng t l v i th i gian thì máy chuy n ñ ng
-1 2
bình n, v i v n t c góc trung bình ω = 21s ; mômen quán tính c a bánh ñà là J = 2kg.m ,
tr ng tâm c a bánh ñà ngay trên tr c quay (hình 3.2)
ω
Phương trình chuy n ñ ng c a bánh ñà:
ω = εt
ω 21
ε= = = 7 rad / s 2
t 3
Mômen c a l c quán tính ñư c tính:
M = J . ε = 2 . 7 = 14Nm
Hình 3.2
3) Tính nh ng áp l c kh p ñ ng và l c cân b ng (ñ t t i ñi m gi a khâu AB theo phương
vuông góc v i khâu này), cho trư c lAB = 0,1m, lBC = lCD = 0,2m. L c c n P2 = P3 = 1000N tác
ñ ng t i trung ñi m các khâu. L c c n P2 hư ng th ng ñ ng xu ng dư i, l c P3 hư ng n m
ngang sang ph i như hình 3.3a. AB, CD th ng ñ ng, BC n m ngang
B
B M 2 C M C b
n
R12 2
1 P2 P2 N
τ f
A N R12 P3
P3 a
3 3 D
D Rτ 3
D d
c e
n
R D3
Hình 3.3a Hình 3.3b Hình 3.3c
Tách nhóm tĩnh ñ nh BCD và ñ t l c vào các kh p ch (hình 3.3b): R21
R12 và RD3. Vi t phương trình cân b ng l c cho toàn nhóm: B
R12 + P2 + P3 + R D3 = 0 (1) Pcb h
phương trình (1) t n t i 4 n s : Giá tr và phương chi u c a 2 l c: A
R12 và RD3. Chia các áp l c này ra thành 2 thành ph n (hình 3.3b)
1
τ
n
R12 = R12 + R12 và R D3 = RD3 + Rτ 3
n
D
Pcb
L y t ng mômen c a các l c ñ i v i ñi m C thu c khâu 2 và thu c khâu 3:
RA1
τ
ΣM (C 2 ) ( Ri ) = R12 .l BC − P2 .l MC = 0 R21
τ
R12 = 0,5 P2 = 500 N 〉 0 Hình 3.3d
τ
Chi u R12 ñã ch n ban ñ u là ñúng.
ΣM (C 3 ) ( Ri ) = Rτ 3 .lCD − P3 .l NC = 0
D

19. Rτ 3 = 0,5 P3 = 500 N 〉 0
D
Chi u Rτ 3 ñã ch n ban ñ u là ñúng.
D
Vi t l i phương trình cân băng l c (1):
R12 + P2 + P3 + Rτ 3 + R D3 + R12 = 0
τ
D
n n
(2)
n n
Phương trình (2) ch còn t n t i 2 n s là giá tr c a R12 và R D3 . Cách gi i ñư c trình bày trên
hình 3.3c.
Véc tơ df bi u th áp l c R D3 có giá tr là 500 2 ( N ) , có chi u như hình v 3.3c
Véc tơ fb bi u th áp l c R D 3 có giá tr là 500 2 ( N ) , có chi u như hình v 3.3c
Vi t phương trình cân băng l c riêng cho khâu 2 ñ tính áp l c t i kh p C: R23 = − R32
R12 + P2 + + R32 = 0 (3)
Phương trình này ch t n t i 2 n s là giá tr và phương chi u c a R32. cách gi i ñư c v hình 3.3c.
Véc tơ fc bi u th áp l c t i kh p C R32 có giá tr là 500 2 ( N ) , chi u như hình v 3.3c.
Bây gi ta ñi tính l c cân b ng ñ t t i ñi m gi a khâu AB:
Phương trình cân băng l c c a khâu 1:
Pcb + R21 + R A1 = 0 (4)
Phương trình này t n t i 3 n s , ñ làm gi m b t n s , ta ñi tìm giá tr Pcb:
l h 0,1 2
ΣM ( A) ( Ri ) = Pcb . AB − R21 .h = 0 Pcb = 2 R21. = 2 . 500 2 . = 500 N
2 l AB 2.0,1
Phương trình 4 ñư c gi i hình 3.3d, và phương chi u c a RA1 ñư c bi u di n như hình v , giá tr
ñư c tính b ng 500N
4) Tính nh ng áp l c kh p ñ ng và moomen cân b ng trên khâu d n 1 c a cơ c u 4 khâu b n
o
l ph ng; cho trư c lAB = lBC / 4 = lCD / 4 = 0,1m; khâu BC n m ngang; các góc ϕ1 = 90 , ϕ2 =
o o
45 và l c c n P3 = 1000N tác ñ ng t i trung ñi m khâu 3 v i α3 = 90 (hình 3.4a). Xét xem
vi c tính nh ng áp l c kh p ñ ng y có ph thu c và v n t c góc khâu d n không? Gi i
thích? B
n 2 C
R12 a
τ 3 d
B 2 C R12 M
1 ϕ1 3 α3
M c
A α3 Rτ 3 D
D
P3
D P3
ϕ2 n b
R D3
Hình 3.4a Hình 3.4b Hình 3.4c
Tách nhóm tĩnh ñ nh và ñ t các áp l c t i kh p ch .
Phương trình cân b ng l c ñư c vi t cho toàn nhóm: B
R21
R12 + P3 + RD3 = 0 (1) Mcb
Chia áp l c t i kh p ch ra làm 2 thành ph n như hình v (hình 3.4b):
τ τ A RA1
ΣM (C 2 ) ( Ri ) = R12 .l BC = 0 R12 = 0
ΣM (C 3 ) ( Ri ) = Rτ 3 .lCD − P3 .l MC = 0
D Rτ 3 = 0,5 P3 = 500 N 〉 0
D Hình 3.4d
Chi u Rτ 3 ñã ch n ban ñ u là ñúng
D
Phương trình cân b ng l c (1) ñư c vi t l i như sau:
P3 + Rτ 3 + R D3 + R12 = 0
D
n n
(2)
Phương trình (2) ch t n t i 2 n s , ho ñ l c ñư c v như hình 3.4c.

20. R D3 = 500 2 N , chi u ñư c xác ñ nh như hình v
R12 = 500 2 N , chi u cũng ñư c xác ñ nh như hình v .
Tính áp l c t i kh p trong C:
Xét s cân b ng c a khâu 2: R32 = − R12 , giá tr : R32 = 500 2 N
Tính mômen cân bbawnoo ñ t trên khâu d n 1:
Ch n chi u Mcb như hình 3.4d.
Mcb = R21 . lAB = 500√ 2 . 0,1 = 50√ 2 Nm
Áp l c t i kh p A: R A1 = − R21 , giá tr b ng 500√ 2 N
Ta l p b ng so sánh:
TT Véc tơ bi u di n Véc tơ th t Giá tr Ghi chú
1 ab P3 1000N
2 bc Rτ 3
D
500N
3 cd n
R D3 500N
4 da n
R12 = R12 500 2 N
5 bd R D3 500 2 N
6 ad R32 500 2 N
Các giá tr trên khi tính không ph thu c vào v n t c góc c a khâu d n, b i vì chúng ta không ñi xác
ñ nh l c quán tính
5) Tính nh ng áp l c kh p ñ ng và moomen cân b ng trên khâu d n 1 c a cơ c u tay quay con
trư t (hình 3.5a), cho trư c lAB = lBC / 2 = 0,1m, AB th ng ñ ng, AC n m ngang. L c c n P3 =
1000N n m ngang cách rãnh trư t m t ño n h3 = 0,058m. Sau ñó nghi m l i K t qu Mcb
b ng phương pháp công su t.
B n B P3
R12 b
2 a
2
1 t x N
C R12 N R12
n
C
A
h3 c
3 h3
P3 3
P3
Hình 3.5a Hình 3.5b Hình 3.5c
Tách nhóm tĩnh ñ nh ra kh i cơ c u và ñ t áp l c vào các kh p ch (hình 3.5b):
Phương trình cân b ng l c ñư c vi t:
B R21
R12 + N + P3 = 0 (1)
Phương trình (1) có 3 n s , ta c n ph i gi m b t các n s . RA1
Chia áp l c kh p ch B ra làm 2 thành ph n (hình 3.5b): Mcb
h
τ τ n A
ΣM (C 2 ) ( Ri ) = R12 .l BC = 0 R12 = 0 R12 = R12
n
Phương trình (1) ñư c vi t l i: P3 + N + R12 = 0 (2) Hình 3.5d
Ho ñ l c ñư c v như hình 3.5c.
Do tam giác ABC là n a tam giác ñ u nên tam giác abc trên hình 3.5c cũng là n a tam giác ñ u:
3 3
R12 = 2000 N , N = 1000 N
3 3
Chi u c a các l c ñã ch n ban ñ u là phù h p.
ð tìm ñi m ñ t c a áp l c N ta vi t phương trình cân b ng mômen c a các l c ñ i v i ñi m C3:

21. P .h 1000.0,058
P3 .h3 − N .x = 0 x= 3 3 = 3 = 0,1m
N 1000
Áp l c N ñ t cách tâm C m t kho ng 0,1m.
ð tính áp l c t i kh p trong C ta vi t phương trình cân b ng l c riêng cho khâu 2:
3
R12 + R32 = 0 R12 = − R32 R12 = R32 = 2000 N
3
Tính mômen cân b ng ñ t t i khâu d n:
Phương trình cân b ng l c t i khâu d n (hình 3.5d):
3
R21 + R A1 = 0 R21 = − R A1 R21 = R A1 = 2000 N
3
Mômen cân b ng có chi u ñư c ch n như hình v 3.5d:
3 0,1 3 B
M cb = R21.h = 2000 = 100 Nm 2
3 2
Chi u Mcb ñã ch n là ñúng. 1
Bây gi chúng ta nghi m l i k t qu trên b ng phương C
pháp công su t. Gi s khâu AB quay v i v n t c góc A
ω1 và ch n chi u Mcb như hình v 3.5e. h3 3
P3
M cb .ω1 + P3 .V3 = 0 (3)
chương 2 ph n phân tích ñ ng h c ta ñã bi t: Hình 3.5e
V B1 = VB 2 = VC 2 = VC 3 = V3
Chi u c a Mcb và ω1 là cùng chi u, chi u c a V3 và P3 là ngư c nhau, do v y t phương trình (3) ta
suy ra:
Mcb . ω1 – P3 . V3 = 0 Mcb = P3 . V3 / ω1 = P3 . ω1.lAB / ω1 = P3 . lAB = 1000 . 0,1 = 100Nm.
Chi u Mcb và giá tr ñã ch n là hoàn toàn ñúng, phù h p v i phương pháp phân tích áp l c.
6) Tính nh ng áp l c kh p ñ ng và mômen cân b ng trên khâu d n 1 c a cơ c u tính sin (hình
3.6a). Cho trư c lAB = 0,1m, ϕ1 = 45o, l c c n P3 = 1000N. Sau ñó gi i bài toán khi rãnh trư t
ch ti p xúc 2 ñi m C’, C’’ v i kho ng cách C’C’’ = 0,2m (hình 3.6b).
B 2 B 2
B
R12 R32
1 R12
C 3 N
A 45o 3 P3 C P3
Hình 3.6a2
Hình 3.6a Hình 3.6a1 B R32
R12
Tách nhóm tĩnh ñ nh (hình 3.6a1) Hình 3.6a3
Kh p trong là kh p t nh ti n, do v y vi t phương trình cân b ng riêng cho t ng khâu. Tách riêng khâu
2 (hình 3.6a2)
R12 + N = 0 R12 = − N 2 l c này song song và ngư c chi u nhau.
L y t ng mô men c a các l c trên khâu 2 ñ i v i ñi m B2 (có giá tr b ng 0) d n ñ n 2 l c R12 , N
tr c ñ i và ñ t tai B (hình 3.6a3)
Xét riêng khâu 3: B
R23 + N + P3 = 0 R23
N2
Chi u phương trình này lên phương P3 và N: N
h
3
C
N = 0 và R23 = − P3 P3
Do v y ta th y r ng chi u các l c ñã ch n trên hình 3.6a3, x
3.6a4 là h p lý và các l c có giá tr N1
R12 = R32 =R23 = P3 = 2000N, N = 0
Do R23 = − P3 và cách nhau m t ño n t o nên m t ng u: Hình 3.6a4

22. R23 .h = P3 . h = M
Chính vì th , áp l c t i kh p C ph i phân b ñ t o thành m t ng u ch ng l i ng u l c M nói trên ñ
khâu 3 tr ng thái tĩnh ñ nh:
R21
N1 + N 2 = N = 0 ; N1 = − N 2 và N1 . x = N2 . x = M B
Xác ñ nh mômen cân b ng:
Xét khâu d n 1 (hình 3.6a5) 1
h
A MCB
Phương trình cân b ng l c: R21 + R A1 = 0
RA1
R21 = − R A1 = 0 , có giá tr là 1000N
Mcb = R21 . h = 1000 . 0,1√2 /2= 50√2 Nm Hình 3.6a5
trư ng h p th hai, xét hình 3.6b
B
B 2 R23
B 2 N2
N2 3
1 P3
3
3 P3
A P3 C’ C’’
C’ C’’
C’ C’’ N1
N1
Hình 3.6b Hình 3.6b2 Hình 3.6b3
Tác nhóm tĩnh ñ nh ra kh i cơ c u (hình 3.6b). Xét riêng khâu 3 (hình 3.6b3)
Phương trình cân b ng l c riêng cho khâu 3:
R23 + N1 + N 2 + P3 = 0
Do 2 l c N1 và N2 cùng phương, cho nên ta có : N1 + N 2 = N
Phương trình trên ñư c vi t l i: R23 + N + P3 = 0 .
Lúc này cách gi i tương t như ph n trên và l y k t qu ñã tính, do N = 0 cho nên: N1 = − N 2 .
Như vây: N1 . x = N2 . x = M
Hay :
N1 = N2 = M / x = R23 . h / lC’C’’ = 1000 . 0,1√2 /2 . 0,2 = 250√2 N
7) Tính nh ng áp l c kh p ñ ng A, B, C, D và mômen cân b ng trên khâu d n 1 c a cơ c u
máy sàng (hình 3.7a). Cho trư c: lAB = lBC/2 = lCD/2 = lDE = 0,1m; ϕ = ϕ23 = ϕ3 = 90o; ϕ4 = 45o.
l c c n P3 = 1000N. B
B C n C
2 E R12 2 ϕ23
ϕ23 R34n t
1 ϕ1 R12
t 4 N h43
A E R34 E
4 P3 3 R43
3
ϕ3 ϕ4 F F
P3 RD3t
D 5 D
5 RD3
n
Hình 3.7a Hình 3.7b Hình 3.7c
Tính cho nhóm tĩnh ñ nh xa khâu d n trư c (nhóm 4,5).
Phương trình cân b ng l c cho nhóm (4,5) (hình 3.7b): R34
N
R34 + N + P3 = 0 (1)
Phương trình này t n t i 3 n s , c n ph i kh b t n s : P3
n τ
R34 = R34 + R34 Hình 3.7d
τ τ n
∑ M ( F4 ) ( Ri ) = R34 .l EF =0 R34 = 0 , R34 = R34

23. Phương trình (1) bây gi ch còn l i 2 n s là giá tr c a áp l c
t i E và áp l c N. Ho ñ l c ñư c v như hình 3.7d. b c
T ho ñ l c ta xác ñ nh ñư c giá tr :
N = P3 = 1000N; R34 = RD = 1000√2 N.
H l c ph ng cân b ng, 3 l c ñ ng quy t i m t ñi m:
Áp l c N, R34, P3 ñ ng quy t i F. Phương chi u ñã ch n ban ñ u
d a
là hoàn toàn ñúng.
Xét ti p nhóm tĩnh ñ nh k khâu d n (2,3)
Phương trình cân b ng l c: Hình 3.7e
R43 + RD3 + R12 = 0 (2)
Phương trình này t n t i 4 n s . Chia áp l c kh p ch B và D ra làm 2 thành ph n như hình3.7c:
τ τ n R21
∑ M (C 2 ) ( Ri ) = R12 .l BC = 0 , R12 = 0 , R12 = R12
B
∑ M (C3 ) ( Ri ) = Rτ 3 .lCD − R43 .h43 = 0
D 1 ϕ1 Mcb
Rτ 3 = 1000 2 .0,1 2 / 2.0,2 = 500 N Chi u ch n ban ñ u là ñúng. A
D RA!
Phương trình cân b ng l c (2) ñư c vi t l i:
R43 + Rτ 3 + R D3 + R12 = 0
D
n
(3) Hình 3.7f
Phương trình này ch có 2 n s , cách gi i ñư c trình bày trên hình 3.7e
Áp l c R12 = RB = 500N ñư c bi u di n b i véc tơ da .
Xét s cân b ng khâu 2:
R12 + R32 = 0 ; R12 = R32 = 500N.
Xét s cân b ng l c c a khâu d n: R21 + R A1 = 0 , R21 = RA1 = 500N
Mcb = R21 .0,1 = 500 . 0,2 = 50Nm
Chúng ta không th tính áp l c kh p ñ ng b t ñ u t nhóm n i v i khâu d n ñư c, vì lúc này
ta chưa bi t ñư c l c tác d ng lên khâu d n và hơn n a, n u th c hi n như v y s không tính ñ n
s tác ñ ng c a các ngo i l c các nhóm xa khâu d n.
8) Tính nh ng áp l c kh p ñ ng và mômen cân b ng ñ t t a khâu d n 1 c a cơ c u cu lít (hình
o o
3.8a). Cho trư c lAB = 0,3m; ϕ1 = 90 ; ϕ3 = 30 , mômen c n M3 = 600Nm ñ t trên culits. Sau
ñó nghi m l i k t qu tính Mcb b ng phương pháp công su t.
ϕ1
A
B B
1 2
2
R12 B R12
B
M3 M3 2 2
ϕ3 3 R32
3 R32
C C
Hình 3.8a Hình 3.8b Hình 3.8c Hình 3.8d
Tách nhóm tĩnh ñ nh (2,3); vì kh p trong là kh p t nh B
R23
ti n cho nên ta vi t và gi i phương trình l c riêng
cho t ng khâu: M3
b,c
Tách riêng khâu 2 (hình 3.8c) ta vi t ñư c:
R12 + R32 = 0 , R12 = − R32 = 0 (1) RC3
t 3 a
L y t ng mô men các l c ñ i v i ñi m B2 : C
∑ M ( B2 ) ( Ri ) = R32 .x = 0 , x=0 (2)
RC3
n
Hai l c R12 và R32 tr c ñ i và ñ t t i B, phương Hình 3.8e Hình 3.8f
vuông góc v i phương trư t BC (hình 3.8d).

24. Xét ti p riêng khâu 3 (hình 3.8e)
R21
τ n
RC 3 + RC 3 + R23 = 0 (3) A
1 B
τ τ M 600 RA1
∑ M ( B3 ) ( Ri ) = RC 3l BC − M 3 ; RC 3 = 3 = = 1000 N Mcb
l BC 0,3.2
n
Phương trình (3) ñư c gi i ho ñ l c (hình 3.8f). RC3 = 0 Hình 3.8g
t
Nghĩa là RC3 = RC3 = R23 = R32 = R12 = 1000N.
Phương chi u c a các l c ñã ch n là h p lý.
Tính mô men cân b ng d t trên khâu d n 1:
o
Xets hình 3.8g: Chi u Mcb ch n trư c, phương l c R21 h p v i phương c a tay quay AB m t góc 30 .
Phương trình cân b ng l c:
R21 + R A1 = 0 , R21 = − R A1 = 0 , R21 = R A1 = 1000 N
Mcb = R21 . lAB /2 = 1000 . 0,3 / 2 = 150Nm.
ϕ1
A
Nghi m l i Mcb b ng phương pháp công su t: 1 B VB3
Ho ñ v n t c cơ c u ñư c bi u di n hình 2
ω1
ω .l
VB2
V B3 = = 1 AB M3
2 2 ϕ3
3
VB ω .l ω
ω3 = 3 = 1 AB = 1 VB2,1
l BC 2.2l AB 4 C
Chi u cùng chi u v i v n t c góc khâu 1
Ch n chi u Mcb cùng chi u v i ω1, ta có:
M cb .ω1 + M 3 .ω3 = 0 , M cb .ω1 + M 3 .ω3 = 0 Hình 3.8h
M 3 .ω3 M 3 .ω1 M 600
M cb = − =− =− 3 =− = −150 Nm
ω1 ω1.4 4 4
Ch nh t chi u Mcb ñã ch n ban ñ u là sai, chi u Mcb s ngư c l i chi u ñã ch n. K t qu phù h p v i vi c
tính toán mômen cân b ng theo phương pháp phân tích áp l c.
9) Tính nh ng áp l c kh p ñ ng và mô men cân b ng ñ t trên cam c a cơ c u (hình 3.9a). T i v trí ti p
o
xuác ñang xeys, biên d ng cam là m t ño n th ng làm v i phương ngang m t góc ϕ1 = 45 , h = a = b =
0,1m và l c c n P3 1000N. Sau ñó hãy gi i bài toán b ng cách thay th kh p cao, r i so sánh k t qu
và phương pháp tính.
P2
P2
C’’ R
C’’
RC’’ h
B
b
b
P2
RC’ R12
C’
2 C’ Mcb
2 1
a
B A
a
B
ϕ1
R12
h
1 A
Hình 3.9a Hình 3.9b Hình 3.9c Hình 3.9d
Tách riêng khâu 2 và ñ t các l c vào (hình 3.9b):
P2 + RC ' + RC ' ' + R12 = 0 (1)
Vì RC’ và RC’’ là cùng phương, do v y h p l c s là RC và chi u R s theo chi u c a véc tơ nào có giá tr l n hơn.
Phương trình (1) ñư c vi t l i:
P2 + RC + R12 = 0 (2)

25. Phương trình (2) ch t n t i 2 n s : ñó là giá tr c a RC và R12. Cách gi i ñư c trình bày trên hình 3.9c.
o
Do ϕ1 = 45 cho nên ta tính ñư c giá tr :
RC = P2 = 1000N và R12 = 1000√2 N
L y t ng mô men c a các l c trên khâu 2 ñ i v i ñi m B2:
∑ M ( B2 ) ( Ri ) = RC '' (a + b) − RC ' .a = 0
RC ' ' = RC ' / 2 . Áp l c RC’ t i ñi m C’ l n hơn áp l c RC’’ t ñi m C’’. Do vây l c t ng RC s mang chi u
c a RC’ . T ñó th y r ng chi u các áp l c ñã ch n là h p lý. Giá c a các l c là:
RC’’ = 2000N và RC’’ = 1000N
Xét hình 3.9d. Moomen cân b ng ñư c ch n như hình v và giá tr ñư c tính:
2
M cb − R21h = 0 , M cb = R21.h21 = 1000 2 .0,1 = 100 Nm
2
Áp l c t i A ñư c tính: R21 + R A1 = 0 R21 = − R A1 , R21 = R A1 = 1000 2 N
Xét trư ng h p thay th kh p cao ta có cơ c u thay th (hình 3.9e):
P2 P2
C’’ C’’
RC’’
b
b
RC’
C’ C’
2 2 a
a
B
ϕ1 B
R12
1
h
A
Hình 3.9e Hình 3.9f
Tách nhóm tĩnh ñ nh (hình 3.9f) , vì kh p trong là kh p quay, ta vi t phương trình cân b ng l c cho toàn nhóm:
P2 + RC ' ' + RC ' + R12 = 0 (3)
Vì RC’ và RC’’ là cùng phương, do v y h p l c s là RC và chi u R s theo chi u c a véc tơ nào có giá tr l n hơn.
Phương trình (1) ñư c vi t l i:
P2 + RC + R12 = 0
Cách gi i hoàn toàn tương t như ph n trư c (hình 3.9c)
Trong trư ng h p thay th kh p cao cho nên s kh p th p nhi u hơn, vi c xác ñ nh áp l c nhi u hơn m t kh p.
Nói cung 2 cách tính ñ u như nhau.
10) Tính nh ng áp l c kh p ñ ng và moomen cân b ng trên khâu d n 1 c a cơ c u trên hình 3.10a. Cho
o o
trư c kích thư c: lAB = lBC /4 = lCD / 2 = lDE / 2 = 0,05m, các góc ϕ1 = ϕ12 = 90 ; ϕ3 = ϕ35 = 45 và l c c n
tác ñ ng n m ngang trên khâu 5 là P5 = 400N.
ϕ12
C B
2 R34 RF R34
3 ϕ3 RF
D ϕ1 1 F
A
E 5 P5
E ϕ35 F 4 P5
5 P5
4
Hình 3.10a Hình 3.10b Hình 3.10c
Tách nhóm tĩnh ñ nh (4,5), ñ t các l c vào, phương trình cân b ng l c cho toàn nhóm:
P5 + R F + R34 = 0 (1)
ða giác l c ñư c v như hình 3.10c, chi u c a các áp l c ñư c xác ñ nh trên ho ñ , có giá tr tương ng:
RF = P5 = 400N, R34 =400√2 N.
Tương t như nh ng bài trư c khi xét riêng khâu 4:

26. p l c R34 ñi qua ñi m E, Phương l c P5 cũng ñi qua E, do v y phương c a RF cũng ph i ñi qua E.
Dĩ nhiên R34 = − R54
Xét nhóm tĩnh ñ nh g n khâu d n (hình 3.10d):
b
B R21
B
C
3 2 R12
n RD3t 1
RD3 c RA1
D R12t
t
RD3n RD3 RD3n A Mcb
a
E
d R12
R43
Hình 3.10d Hình 3.10e Hình 3.10f
Phương trình cân b ng l c cho toàn nhóm:
R43 + R D3 + R12 = 0 Hay R43 + Rτ 3 + RD3 + R12 + R12 = 0
D
n τ n
(2)
∑ M (C 2 ) ( Ri ) = Rτ 3 .lCD − R43 .lCE = 0
D
l
Rτ 3 = R43 CE =
400 2
D = 200 2 N
lCD 2
Chi u ñã ch n ban ñ u là ñúng.
τ τ
∑ M (C3 ) ( Ri ) = R12 .l BC = 0 , R12 = 0
Phương trình (2) ñư c vi t l i như sau:
R43 + Rτ 3 + RD3 + R12 = 0
D
n
(3)
n
Phương trình này t n t i 2 n s là giá tr c a RD3 và giá tr c a R12, cách gi i ñư c trình bày trên hình 3.10e.
Phương chi u c a các l c ñã ch n là h p lý. Giá tr ñư c tính tr c tiép trên ho ñ l c:
RD3 = R12 = 400N
Xét s cân b ng c a khâu 2 : R12 + R32 = 0 2 l c này ngư c chi u nhau và có giá tr chính b ng 1000N.
Tính l c khâu d n.
Xét hình 3.10f . Phương trình cân b ng l c:
R21 + R A1 = 0 , R21 = R A1 = 400 N
Ch n chi u Mcb như hình v :
Mcb = R21 . lAB = 400 . 0,1 = 40Nm
11) Tính áp l c kh p ñ ng tai B (kh p quay gi a bánh răng 2 và c n C) và mômen cân b ng Mcb trên c n
C c a cơ c u bánh răng hành tinh (hình 3.11a), dư i tác ñ ng c a mômen c n trên khâu 1: M1 = 20Nm,
cho trư c mô ñun c a các bánh răng m = 20mm, góc ăn kh p tiêu chu n, s răng các bánh: z1 = z2 =
20; z3 = 60.
B 2
2 B
2
C
A
M1 1 A 1
M1
3
3
Hình 3.11a Hình 3.11b
Mômen cân b ng tác ñ ng lên c n C ñư c tính t phương trình cân b ng công su t:
Mcb . ωC + M1 . ω1 = 0 Mcb = -M1 .ω1 /ωC
Xét chuy n ñ ng tương ñ i c a cơ h ñ i v i c n C:
ω1C = ω1 − ωC và ω3C = ω3 − ωC

27. ω1 − ω C ω z
= 1− 1 = − 3
ω 3 − ωC ωC z1
ω1 z
= 1+ 3 = 4
ωC z1
Mcb = -20 . 4 = - 80Nm
Ch ng t Mcb nư c chi u v i M1 .
Ta có R2C = R02 = R B
Xét s cân b ng mô men c a c n c.
RB .rc + M cb = 0
V i rc = m (z1 + z2 )/2 = 20 (20 + 20)/2 = 400mm
V y: RB = - Mcb /rc = - 80/0,4 = - 200N
12) Tính áp l c kh p ñ ng B (kh p gi a các bánh răng 2 và 2’ v i c n C) và moomen cân b ng trên khâu
d n 1 c a cơ c u bánh răng gành tinh (hình 312), dư i tác ñ ng c a moomen c n trên c n C: Mc =
56Nm; cho trư c môñun c a c p bánh răng 1 và 2 là mI = 5mm, c a c p bánh răng 3 và 2’ là mII =
0
8mm, góc ăn kh p α = 20 và các s răng Z1 = 28, Z2 = 84, Z2’ =20, Z3 = 50.
2
Xét s cân b ng moomen c a c n C:
RB.rc + Mc = 0 2’
V i rc = m (z1 + z2 )/2 = 5 (28 + 84)/2 = 280mm B
RB = - Mc / rc = - 56 / 0,28 = -200N
Mômen cân b ng ñ t trên khâu 1 ñư c tính: C
Mcb.ω1 + Mc.ωc = 0
3
Mcb = -Mc.ωc / ω1 = - Mc.1/ i1c = -Mc . 1/ (1 – i1 c) =
= -Mc . 1/ (1-( Z3/Z2’)(Z2/Z1))
Mc
1
MCb = - 56 . 1/ (1- (50/20)(84/28)) = - 8,6Nm 3
Hình 3.12