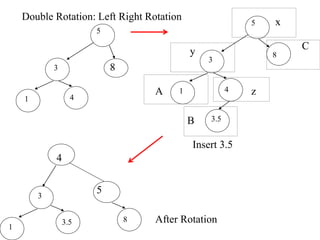
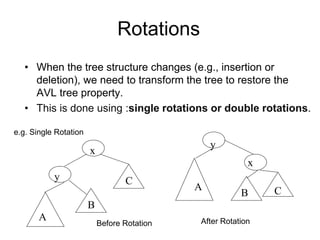
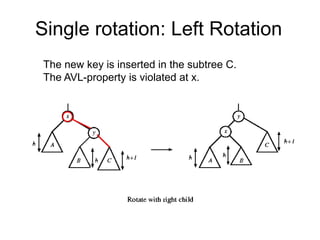
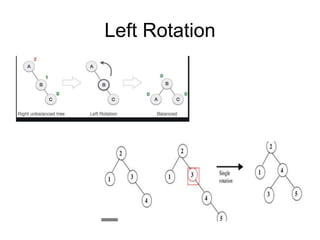
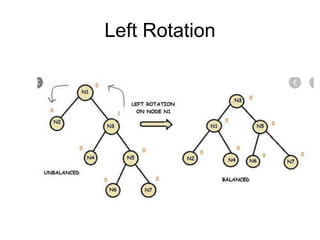
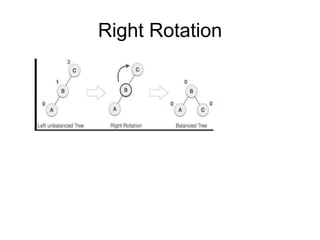
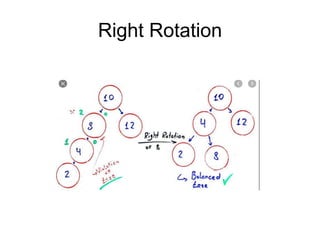
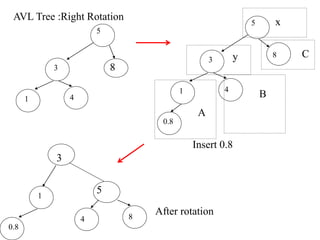
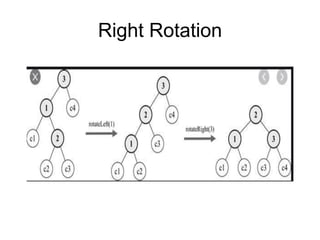
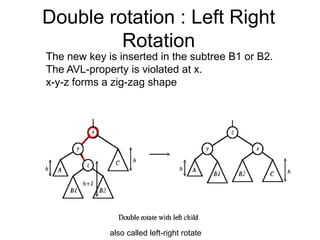
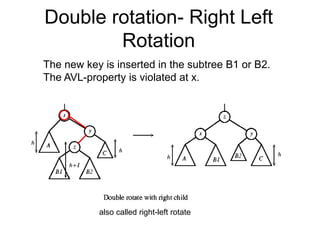
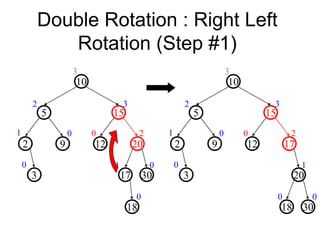
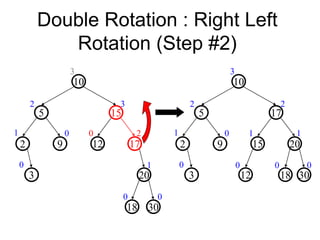
- AVL trees are self-balancing binary search trees where the heights of the two child subtrees of every node differ by at most one. - When a node becomes unbalanced due to an insertion or deletion, rotations are performed to restore the balance property. Single and double rotations are used to rebalance the tree. - Insertions and deletions in AVL trees take O(log n) time due to rebalancing, compared to O(n) time for unbalanced binary search trees. Rotations are used to restore the balance property during updates.

1. Balanced Trees
AVL TREE

2. AVL Trees
• AVL tree is a Balanced Binary Search Tree
• Balanced Factor : Balanced Factor of a
node is the absolute difference in heights
between left and right sub trees
• AVL tree is defined is a Binary Search
Tree tree such that, for each node,
balanced factor ≤ 1

3. AVL-Trees
An AVL-tree is a BST with the property that at
every node the difference in the depth of the
left and right subtree is at most 1.(0,1,-1)
OK
not OK
Two binary search trees: (a) an AVL tree; (b) not an AVL tree (unbalanced
nodes are darkened)

4. AVL Tree
Insertion/Deletion in an AVL-tree is more
complicated: Inserting/Deleting a new element may
break the balance of the tree.
But we can't just place the new element somewhere
else, we have to maintain the BST property.
Solution: insert in standard place, but then
rebalance the tree using the operation “ROTATION”.
Thus, many operations (searching, insertion, deletion) on
an AVL tree will take O(log N) time.

5. Rotations
• When the tree structure changes (e.g., insertion or
deletion), we need to transform the tree to restore the
AVL tree property.
• This is done using :single rotations or double rotations.
x
y
A
B
C
y
x
A
B C
Before Rotation After Rotation
e.g. Single Rotation

6. Single rotation: Right Rotation
The new key is inserted in the subtree A.
The AVL-property is violated at x
height of left(x) is h+2
height of right(x) is h.

7. Single rotation: Left Rotation
The new key is inserted in the subtree C.
The AVL-property is violated at x.

8. Left Rotation

9. Left Rotation

10. Right Rotation

11. Right Rotation

12. 5
3
1 4
Insert 0.8
AVL Tree :Right Rotation
8
0.8
5
3
1 4
8
x
y
A
B
C
3
5
1
0.8
4 8
After rotation

13. Right Rotation

14. Double rotation : Left Right
Rotation
The new key is inserted in the subtree B1 or B2.
The AVL-property is violated at x.
x-y-z forms a zig-zag shape
also called left-right rotate

15. Double rotation- Right Left
Rotation
The new key is inserted in the subtree B1 or B2.
The AVL-property is violated at x.
also called right-left rotate

16. So?
Rotation does not change the flattening, so we still
have a BST.
But the depth of the leaves change by -1 in A, stay
the same in B, and change by +1 in C.

17. Double Rotation : Right Left
Rotation (Step #1)
20
9
2
15
5
10
30
17
3
12
1
1
2
0
0
2 3
3
0
0
18
0
17
9
2
15
5
10
20
3
12
1 2
0
0
2 3
3
1
0
30
0
18
0

18. Double Rotation : Right Left
Rotation (Step #2)
17
9
2
15
5
10
20
3
12
1 2
0
0
2 3
3
1
0
30
0
18
0
20
9
2
17
5
10
30
3
15
1
0
1
1
0
2 2
3
0
0
12
0
18

19. 5
3
1 4
Insert 3.5
Double Rotation: Left Right Rotation
8
3.5
5
3
1 4
8
4
5
1
3
3.5 After Rotation
x
y
A z
B
C
8

20. Deletion of Node
Steps
1.Delete a node ( As in BST)
2.Balance the AVL Tree

21. Search is Similar to BST

22. Applications