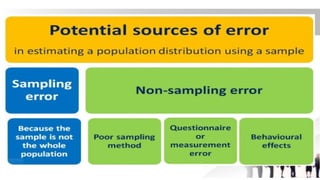
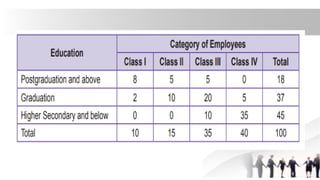
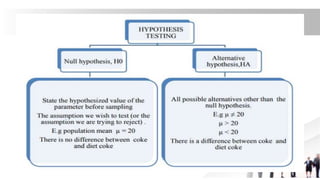
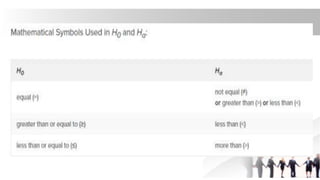
The document covers key concepts related to sampling and hypothesis testing, including the definitions of population, sample, sampling frame, and common sampling methods such as probability and non-probability sampling. It details the sampling process, including defining target populations, determining sample sizes, and addressing sampling errors. Furthermore, it discusses various sampling techniques like simple random sampling, systematic sampling, cluster sampling, and quota sampling, alongside the significance of estimating errors in research methodologies.